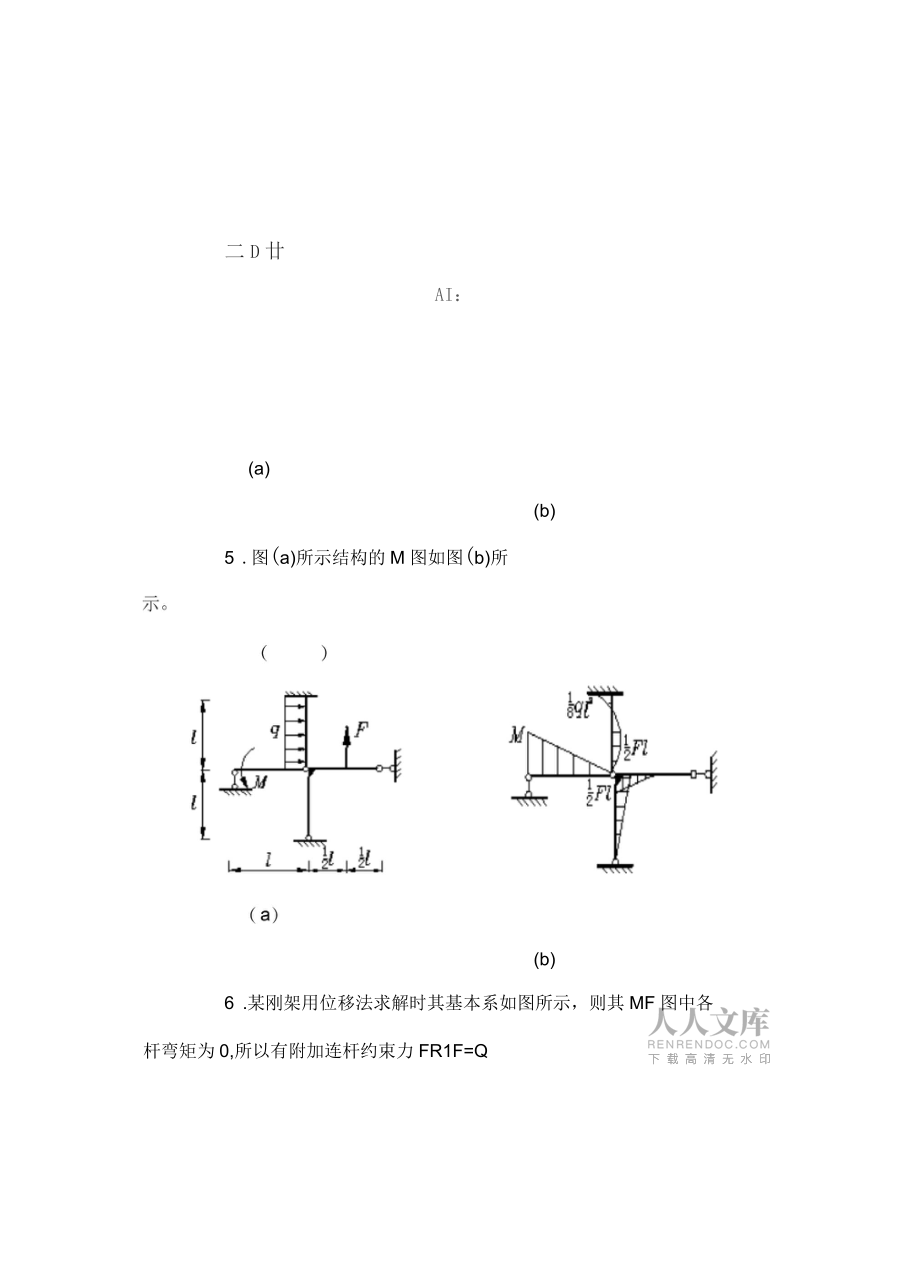
1、第五章位移法和力矩分配法一、判斷題（“對”打一“錯”打X）1 .位移法和力矩分配法只能用于求超靜定結構的內力，不能用于求靜定結構的內力。（）2 .用位移法求解圖示結構基本未知量個數最少為5。（）3.對于圖（a）所示結構，利用位移法求解時，采用圖（b）所示的基本系是可以的。（）(a)（b）4.圖示兩剛架僅在D點的約束不同，當用位移法求解時，若不計軸向變形則最少未知量數目不等，若計軸向變形則最少求知量數目相等。二D廿AI：(a)(b)5 .圖(a)所示結構的M圖如圖(b)所(b)6 .某剛架用位移法求解時其基本系如圖所示，則其MF圖中各桿彎矩為0,所以有附加連桿約束力FR1F=QF7 .圖a結構用

2、位移法計算的基本系如圖b,則其加2圖如圖c所(a)(b)()(c)8 .圖示連續梁在荷載作用下各結點轉角的數值大小排序為伊A；B；C：D.()q9 .圖示兩結構(EI均相同)中MA1等。(a)(b)10 .下列兩結構中MAffi(a)(b)11.圖示結構結點無水平位移且柱子無彎12 .圖示結構下列結論都是正確的:例=。北=。，知必=Q"即=（上拉）82E113 .用位移法計算圖示結構，取結點B的轉角為未知量T1,則14 .圖a對稱結構（各本f剛度均為EI）可以簡化為圖b結構（各桿剛度均為EI）計算。（）F/2(a)(b)15 .圖a對稱結構可以簡化為圖b結構計算（各桿剛度不變）18.

3、圖示結構中有c點水平位移L "和BE桿B點彎矩()q(b)16 .圖a對稱結構可以簡化為圖b結構計算(b)(a)17 .圖（a）所示對稱結構，利用對稱性簡化可得計算簡圖，如圖（b）所示EI(b)(a)19.圖示結構的彎矩圖與是否有AB桿和BC桿無關。20.21.二根據力矩分配法，圖示結構最后彎矩有關系：2()22.12(b)三、填空題2.圖示結構用位移法求解時，基本未知量個數最少為。當支座A有垂直于AB的向右下方的單位位移時,3.圖示單跨梁當A支座有垂直向下單位位移時，MAB=MAB=。當支座4.根據互等定理知道位移法典型方程中的副系數kij=kji,該互等定理可互等定理導出。（各桿

4、桿長l ,剛度為EI）5 .若如圖示剛架在mB的作用下，B結點產生單位轉角。則mB=,其中系數項 k11 =6 .對圖示結構用位移法求解時，其典型方程一般形式為FR1F=FR1F=7.某結構用位移法求解時,基本系如圖所示，則典型方程中的系數k11=,k12=,k22=FR2F=FEI135FP8.圖示結構，EI二常數，已知結點C的水平線位移為110457,則結點B的角位移B=B=轉向為。（填順時針或逆時針）且側受寸匚 MCD=,側受拉10.欲使圖a和圖b中的MB=MB,則如二盤（逆時針）9.圖不結構，EI=常數，已知結點D的轉角64秋則MDB=,Q11 .圖示結構A點的彎矩MA=。/e/=cZ

5、以=8色9l_I_'mi12 .利用位移法判斷結點A的轉角/A的轉向為。F我C-1'.1)15.16.17.14.利用位移法概念求圖示結構支座反力FRD二*阪、圖示為一連續梁的位移法基本系，則系數k12=,k22=/卷二3上"初在側受拉)13.已如圖示結構中11，則C點水平(4移c=BC圖示結構用位移法計算，取結點B的水平位移為未知量，則系數k11=kN-m.F2KMTEIEA=flOkN/見ei通數圖示對稱剛架受對稱荷載，由位移法可知，MCB=kNI-m,MAB=JD111i11i11118.圖示結構，FQCB二,FQBE二4FaEliEliEI；2El!2EIs1

6、側受才i,MBC=HA口工E工三8F3MEA=mclG3mrEJ3mz，河.J21.力矩分配法中，傳遞系數表示當桿件近端有轉角時，的有關。22.圖示結構用力矩分配法計算時，J與的比值，它與桿件遠端A點的不平衡力矩m=。'BM/123.用力矩分配法計算圖示結構，則分配系數1AB=,傳遞系數用對自剛度JLA耳CDCAC=24,圖示結構用力矩分配法求解時，其結點不平衡力矩mk=25.圖示結構的彎矩MBA二虹,MBC=。（J順時針為正）X一|26.用力矩分配法計算圖示剛架，則分配系數,傳遞系數CBA=。（各桿l,EI相同）27.力矩分配法與位移法在消去附加剛臂作用的做法上的不同是：位移法通過滿

7、足典型方程使各剛架上反力矩為零，而力矩分配法則一、是非題位移法取結點位移為基本未知量、附加約束的結構為基本結構,所以也可以用于求靜定結構內力,力矩分配法亦類似，但它只可求解無結點線位移的靜定結構。力法須解除多余約束，故不可用于求靜定結構內力。較上方的剛結點轉角可不取未知量，該題基本未知量數最少為3個（一個線位移、兩個角位移3、，. 是可以的，但未知量數不是最少的。矩陣位移法電算中就是這樣處理的。4、V.不計軸向變形基本未知量為（a）4個、（b）3個，計軸向變形均為6個。件可知O中間的較無線位移并將結構分為三個部分，它們之間無力矩的傳遞，可獨立畫出各自的彎矩圖。根據截面剪力平衡條7、，.注意此時

8、斜桿只有剛體位移無彎矩。8、，.可根據下列步驟作定性分析：（1）草繪彎矩圖和撓曲線圖，（2）按超靜定結構求位移的方法，取三跨簡支梁為靜定基本系，（3）分別建立虛力狀態計算各跨簡支梁兩端轉角，根據圖乘法分析可比較出各支座處轉角的大小。9、V.按力矩分配法計算，兩結構的分配系數、傳遞系數和固端彎矩均相同，故可得出結論。用位移法分析也可以得出該結論。10、，.兩結構相對線剛度相同，分配系數、傳遞系數和結點不平衡力矩均相同11、，.此結構因水平桿£I二e,故剛結點無轉角，又若有結點水平線位移，則橫梁在水平方向無法平衡，故也無結點水平位移，所以柱子無彎矩他二Q；若A：*Q則ABC桿水平方向無法

9、平衡；由于以上兩點,BD桿無彎矩;AB桿相當于B端固定A端較支，故有3El_2EI13、，.該結構無結點線位移.位移法固定狀態下兩本fB端抗彎勁度為，故得,E114、X.因荷載反對稱，故在半結構中，原來位于對稱軸上的桿的剛度應取為215、，.對稱結構受對稱荷載作用，位于對稱軸上兩剛結點只能上下移動，但受兩斜桿支撐又不能上下移動，故相當于固定。16、，.對無支座的平衡體，可假設某點相對不動（即固定），對該結構設最下面結點相對固定，其半結構即圖（b）.17、V.因對稱，兩剛結點處無轉角和水平位移，不僅如此，豎桿任一點也無轉角、無水平位移和無彎矩。簡化后的半結構在兩剛結處位移條件與原結構相同，故兩橫

10、梁彎矩不變。18、X根據ABCDZK平方向平衡可知,E點處無水平約束力，故但是FEG部分不對稱,E點有水平位移要引起水平位移19、V.因結構對稱受對稱荷載，B結點無轉角和無位移，只有水平桿有彎矩，去掉兩斜桿后，以上狀態不變。20、V. 結構中D點無轉動和移動，可視CD桿為兩端固定梁來考慮（當C結點轉動時）121、X. A端向B端的傳遞系數，只有當1 ,第一跨相當于兩端固定梁，可求出右端彎矩為B端固定無轉動時才等于2 ,而現在B端為彈性的，故不成立。尤12 ，其他部分可簡化為圖（功計算。22、V.根據條件23、V.力矩分配法固定狀態下，BC桿為兩端固定梁，求出支座位移作用下的固端彎矩即可疊加出不

11、平衡力矩。24、V.左邊F簡化為結點外力偶，右邊F簡化為桿端外力偶，簡化去掉的桿的彎矩按靜定法求出。二、選擇題1、B.左邊較上剛結點轉角可不取為未知量，右邊較連接的剛結點轉角要取為未知量。2、C.其他三圖結構均有結點線位移。3、D.圖A結點無轉角，若有水平線位移，則橫梁在水平方向無法平衡；圖B由對稱性，可知無水平線位移；圖D結構中間的兩剛結點有線位移，獨立線位移1個。4、C.組合結點較端轉角不是基本未知量。5、A.結點A無線位移，又假設A點不能轉動，則B、C點也不能轉動和位移，故只有一個基本未知量。C.A.BA桿B端抗彎勁度為0。C.A點向右，B點向上，AB桿轉的角度為;AB桿兩端垂直桿軸的相

12、對位移為桿長乘轉角，即桿件按兩端固定梁計算得桿端彎矩O9、B.根據位移法，要期二0,必須自由項3i,即可求得。12i10、C.左邊四個豎桿對凡11的貢獻均為/;右邊四桿中除右下角的桿子外,對仆11的貢獻均為11、D.結點上集中力F要考慮。12、D.應等于各桿A端抗彎勁度之和，右橫梁抗彎勁度為0。13、A.應等于各桿剛結點處的固端彎矩之和，右邊的集中力可簡化成結點集中力偶6kNm14、A.圖b結構A結點無線位移，受結點集中力作用時結構無彎矩。圖a結構則非。15、B.由ABCEgB分水平方向平衡條件知E點無水平約束力，故此部分為對稱受力狀態,F故有16、C.q不引起M或.f可視為反對稱荷載，由此求

13、出底部兩水平反力為2F,則可求出17、C.由對稱知18、19、20、21、22、23、24、.B點無線位移，則A點的彎矩為OFl_B點的一半.故有D.因為圖D結構有側移。A.C.B.A.C.A.注意桿AD的抗彎勁度為0,AB桿與兩端固定梁一樣。注意分配系數的計算式并非它的定義。分配系數、傳遞系數是結構固有的，與荷載無關。1水平桿無彎矩，又剛結點無線位移故按2傳到固定端。用力矩分配法分析，圖b結構兩桿分配系數和傳遞系數均相同，故有4和C截面彎矩相等；其他等式均不成立。按力矩分配法概念，作用結點C的外力偶矩全部分配給CD桿C端（分配系數"CD三、填空題1、6.由于結構約束不對稱，雖然受力

14、對稱但位移不對稱，有四個水平位移和3個豎向位移未知量，考慮到結構最終保持對稱的變形狀態。A,C兩點豎向位移相同，故基本未知量為6個。2、1.若將下面一個剛結點加剛臂約束住，則上面一個剛結點就不能轉動和移動。3、0,A支座向下移動，AB桿向下平移；A支座垂直于桿軸移動時，可按一端固定，另一端較支處理;座向右水平移動,固端彎矩。B點向上，AB桿轉過的角度為,引起兩端相對位移為,進而再按一端固定一端錢支計算4、反力，虛功。祝應等于各桿B端抗彎勁度之和。6E1F"，0.6E1該結構只有一個水平線位移未知量。6E15El注意在一一作用下，斜桿為剛體平移，無彎矩。818457,順時針.建立一個位

15、移法方程：七而+上"工+/f=0即可求出（即理）二：.二，二二及F作用的結果相疊加得至限也可按兩端固定梁 AD,受2io、5.根據M蛇二%仃可知麴二包再由位移法可知% 二 F'f由此可得結果111213140.因為中間較結點無線位移，又無力矩的傳遞，故水平桿無彎矩。順時針.20根據稱，四個角點轉角大小相同.設物為順時針方向，由于A結點的為負值，故 Si為正值即順時針。三二.10FA點彎矩%£由人廣品和F共同引起.按一端固定一端錢支梁計算。6i.先求出 色3 1 L設為順日t針向）時水平連桿反力久二+"門3,再求B結點轉角£.兩者相乘再加上力F移到

16、B點后直接產生的連桿反力。8£Z15、計算中除要計算排架 ABDEM''ll的貢獻，還要計及BC桿對“11的貢獻。3EI16、3E1的貢獻。應同時考慮彈簧對17、20, 0.根據對稱性取半結構，它為無側移鋼架 舊結點為較，所以荷載彎矩圖即為最后彎矩圖118、-2F, 2F兩次利用對稱性簡化，得受F作用的 4剛架為靜定剛架，即可得解193kN-m ,左，0.由對稱性桿BF軸力為0;A、E結點無轉角，只有水平位移，故結點B為柱子的反彎點,沒有彎矩，只有剪力（為即可求得C點彎矩.200 , 0此結構為對稱于原點（C點）的結構，但荷載為反對稱（繞C點在平面內轉IglJ ,BC和CD上的荷載大小相等、方向相反),故Fa16,右,64,下.可按計算，簡單地也可按單跨梁分別計算截面C上不能有對稱性內力。在此情況下,c截面的剪力和軸力均屬對稱性內力（截面兩邊的剪力或軸力，在繞c轉1UU后大小相等方向相同）故它們均為0。注