1、等腰三角形的判定1、等腰三角形的概念 2、等腰三角形的性質是什么有兩邊相等的三角形叫等腰三角形（1）在同一個三角形中，等邊對等角（2）三線合一（頂角平分線、 底邊上的中線、底邊上的高互相重合） 等腰三角形：一、復習回顧：若B=C,問 ABC是否是等腰三角形。請說明理由。BACD1243二、探究新知：解：作BAC的角平分線AD交BC于點D AD 是BAC的角平分線 1=2在ABD和ACD中B=C 1=2 AD =AD ABD ACDAB=AC(全等三角形的對應邊相等）等腰三角形的判定定理： 在一個三角形中，如果有兩個角相等，那么它們所對的邊也相等。在ABC中， B=C AC=AB簡寫成： “在同

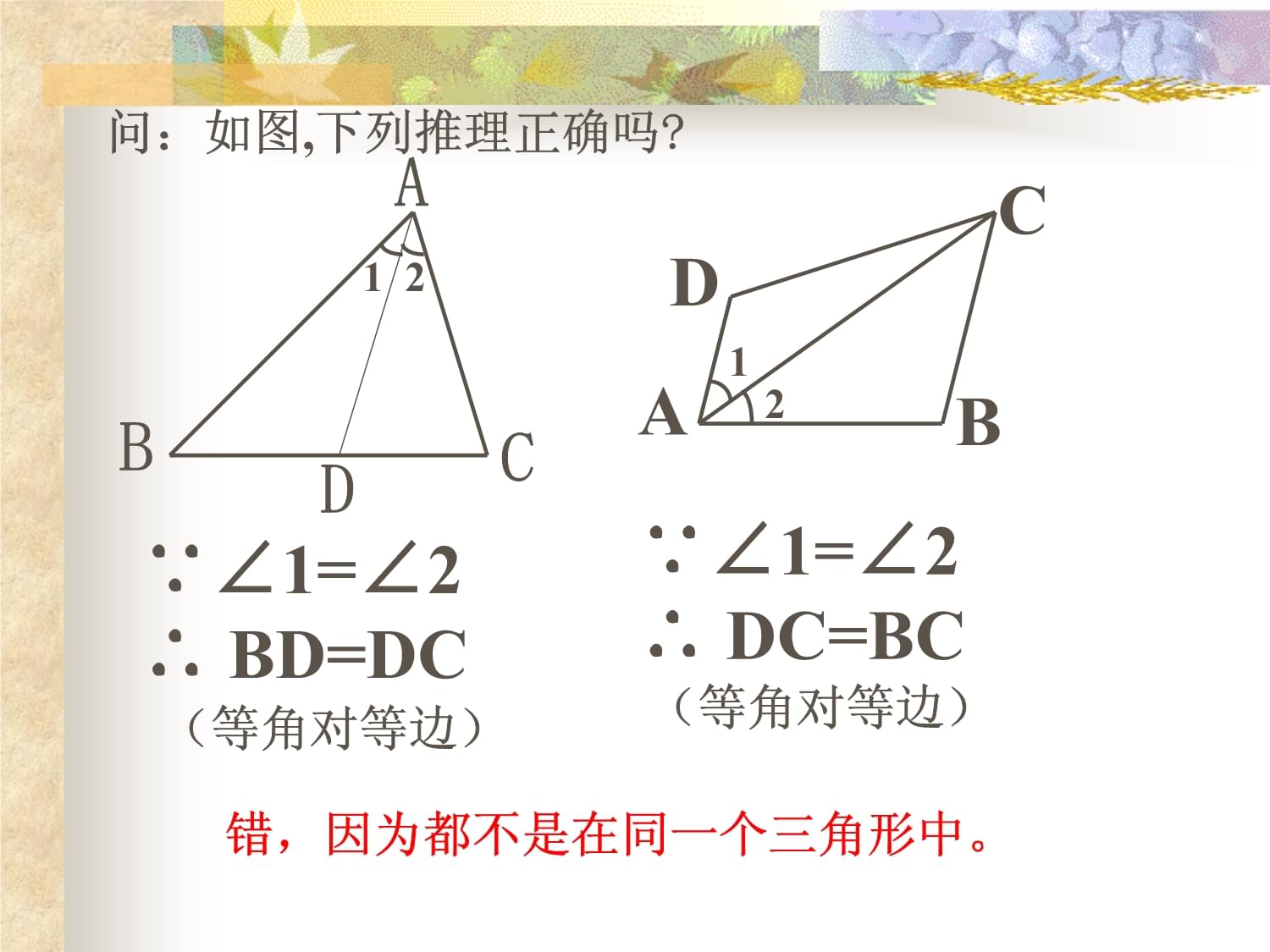
2、一個三角形中，等角對等邊”ACB二、探究新知： 問：如圖,下列推理正確嗎? ABCD211=2 BD=DC（等角對等邊）1=2 DC=BCABCD21（等角對等邊）錯，因為都不是在同一個三角形中。解： DAC= ACB+ ABC （三角形外角的性質） ABC= DAC - ACB =60 - 30 =30 ABC= ACB AB=AC（在同一個三角形中， 等角對等邊）即AC的長就是河寬。 三、范例講解：生活實例：一次數學實踐活動的內容是測量河寬，如圖，即測量A, B之間的距離。小明想出了一個方法：從點A出發，沿著與直線AB成60 角的AC方向前進至C , 在C處測得 C= 30 ，量出AC的長

3、，它就是河的寬度。這個方法正確嗎？請說明理由。30 ABCD60 想一想：還有其它測量河寬的方法嗎？三、范例講解：例2、如圖，BD是等腰三角形ABC的底邊AC上的高，DEBC,交AB于點E. 判斷BDE是不是等腰三角形，并說明理由.EACBD123解： BD是等腰三角形ABC的 底邊AC上的高 1= 2 （等腰三角形三線合一） DEBC 1= 3 (兩直線平行，內錯角相等） 2= 3BE=DE (在同一個三角形中，等角對等邊） BDE是等腰三角形如果BD是底邊上的中線，那結論又如何？例3、 如圖ABC中，ABC=ACB, BO平分ABC，CO平分ACB， 在這張圖上，由這兩個已知條件，你自己能

4、導出什么結論？三、范例講解：ABCO變式1： 過點O作一條直線EFBC，與AB交于E，與AC交于F，（1）圖中有幾個等腰三角形?（2）EF和EB、FC之間有什 么關系? 說明理由.C123456ABOFE解：（1）圖中有5個等腰三角形EB=EO、OF=FC（在同一個三角形中等角對等邊）（2）O是ABC、ACB的平分線交點， 1= 2、4=5 （角分線定義） EF BC（已知） 3=2、4=6（兩直線平行，內錯角相等） 3=1、5=6（等量代換） EF=EO+OF EF=BE+CF等腰ABC、等腰AEF、等腰BEO、 等腰COF、等腰BOC 三、范例講解：變式2： 現在把AB、AC變成不相等，其

5、它條件不變，想一想，這個圖形中還有沒有等腰三角形，有的話有幾個，EF和EB、FC之間還有沒有關系，有的話又是一種怎樣的關系？C123456ABOEF解：（1）圖中有2個等腰三角形 等腰BEO、 等腰COF（2）O是ABC、ACB的平分線交點， 1= 2、4=5（角分線定義）EF BC（已知） 2=3、4=6（兩直線平行，內錯角相等） 1=3、5=6（等量代換）BE=EO、OF=CF（在同一個三角形等角對等邊） EF=EO+OF EF=BE+CF三、范例講解：1、如圖，在ABC中， B=C，AB=10cm, 求AC的長。四、練習鞏固、應用新知4、已知:如圖,DE BC, 1= 2. 說明AB=A

6、C的理由，圖中有幾個等腰三角形，BD =CE嗎？ABCDE122、在ABC中，A=40, B=70 （1）求C等于幾度？ （2）ABC是什么三角形？為什么？3、如圖，在ABC中,AD BC, 已知點E在BA的延長線上，并且1=2, 問：ABC是什么三角形？為什么？ABCED12如果AD=4cm，則BC= cm.5、已知:如圖,A=36, DBC=36，C=72,1= 度, 2= 度，圖中有 個等腰三角形。723634如果過點D作DEBC,交AB于點E,則圖中有 個等腰三角形. 5 你能不能把 ABC分成更多的等腰三角形呢？E36236172ABCD五、練習鞏固、應用新知6、如圖,C表示燈塔,輪

7、船從A處出發以每小時18海里的速度向正北(AN方向)航行,2時后到達B處,測得C在A的北偏西40方向,并在B的北偏西80方向.求B處到燈塔C的距離. ABCN11= A+ C A= C=40解： A=40 , 1 =80 AB=BC （在一個三角形中，等角對等邊） AB=182=36, BC=36答: B處到燈塔C的距離是36海里.4080五、練習鞏固、應用新知 等腰三角形性質定理 等腰三角形判定定理 條 件 在一個三角形中，如果有兩條邊相等 在一個三角形中，如果有兩個角相等結 論 這兩條邊所對的兩個角相等 這兩個角所對的兩條邊相等簡 稱在同一個三角形中等邊對等角在同一個三角形中等角對等邊 推

8、理形 式 AB=AC， B=C B=C， AB=AC 六、小結反思：1、等腰三角形的性質定理與判定定理的區別與聯系2、通過各例和變式練習，使學生體會到由“角平分線”、“平行線”常常可以找到“等腰三角形”，并解決各類問題。 已知:如圖,在ABC中，BO、CO分別平分ABC、ACB并交于點O,過點O作 ODAB, OEAC,BC=16,求: ODE的周長變式3：123456三、范例講解：FEOCBA已知:如圖,在ABC中，BO、CO分別平分EBC、FCB并交于點O,過O作 EFBC. 請問EF與EB、CF又有什么樣的關系，說明理由.變式4：三、范例講解：123654FEGOCBA已知:如圖,在AB

9、C中，BO、CO分別平分ABC、ACG并交于點O,過O作 OEBG,交AB于點E,AC于點F.請問EF與EB、CF又有什么樣的關系，說明理由.變式5：三、范例講解：543621已知:如圖,在ABC中，CF、CE分別平分ACB、ACD,CF交AB于點F,過點F作 EFBD,交AC于點G變式6：三、范例講解：請說明 FG=GE 的理由123456例3、如圖，在ABC中,B=C，D是BC上任意一點，DEAC,DFAB，AB=4cm，求四邊形ADEF的周長。解： DEAC（ ） 1= C （ ） B=C（ ） B=1 （ ） - = - -（ ） DFAB（ ） 2= - （ ） C=B（ ） C=2 （ ） DF=-（ ） AE+ED+DF+AF=AE+BE+ FC+AF =-+- B=C（ ） AB