曲面在空間解析幾何中被看作點的軌跡.曲面方程的定義：一、空間曲面方程如果曲面

與三元方程F

(x,y,z)

0

有下述關系：曲面上任一點的坐標都滿足方程；不在曲面上的點的坐標都不滿足方程；那么,方程F

(x,y,z)

0

就稱為曲面

的方程,而曲面∑稱為方程的圖形.F

(x,

y,

z)

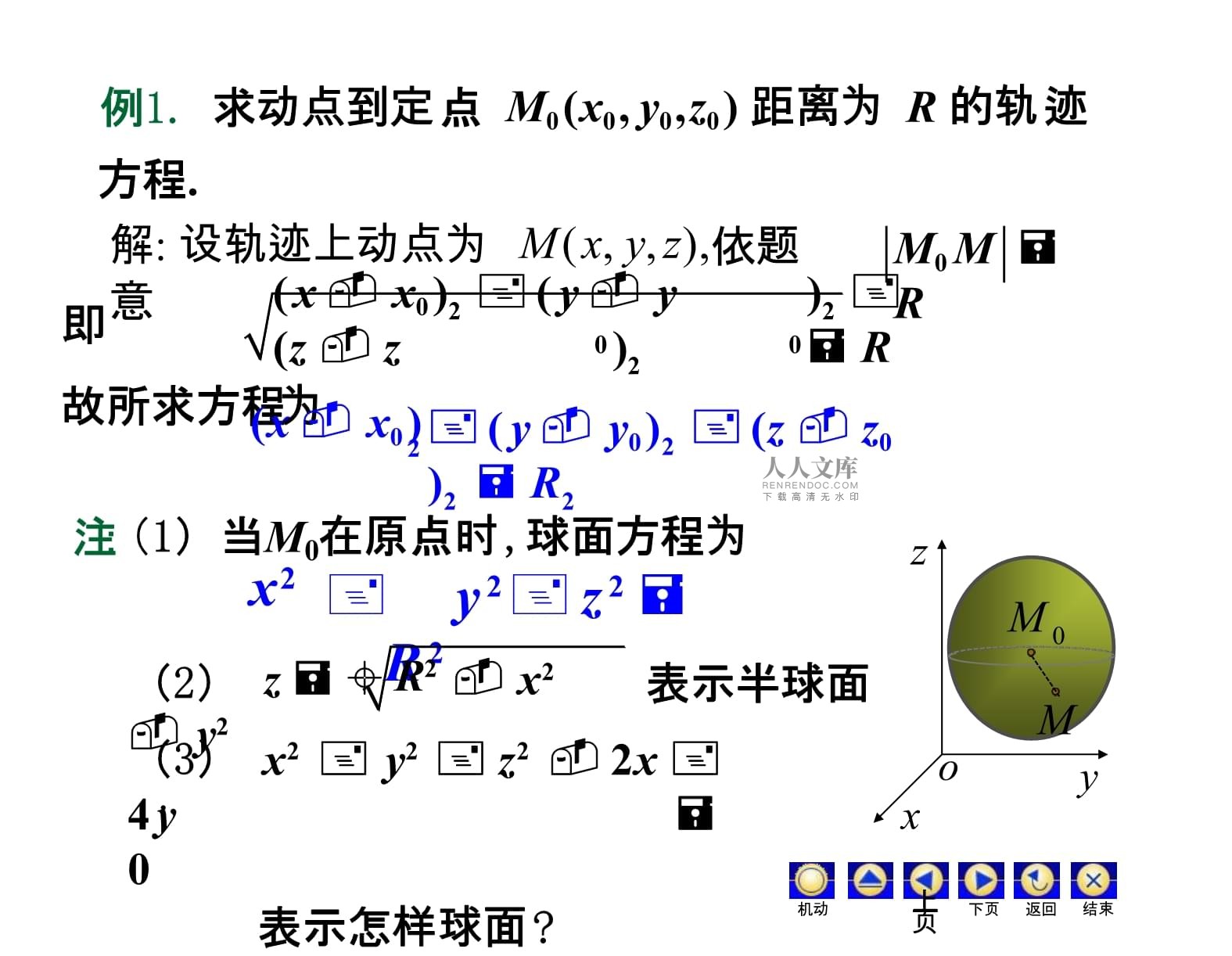
0zxo上機動頁下頁返回結束例1.求動點到定點

M0

(x0

,y0

,z0

)距離為

R的軌跡方程.解:設軌跡上動點為M

(x,y,z),依題意即xyzoM0M表示半球面（3）

x2

y2

z2

2x

4

y.

0表示怎樣球面?(

x

x0

)2

(

y

y

)2

(z

z

)2

R0

0

(

y

y0

)2

(z

z0

)2

R2x

2

y

2

z

2

R

2故所求方程(x為

x0

)2注：（1）當M0在原點時,球面方程為M0

M

RR2上機動頁下頁返回結束（2）z

x2

y2定義旋轉一周所成的曲面,稱為旋轉曲面.線稱母這條定直線叫旋轉曲面的軸.此曲

線.例如:一條平面曲線繞其平面上的一條直線母線軸二、旋轉曲面上機動頁下頁返回結束建立yoz面上曲線C

繞

z

軸旋轉所成曲面的方程:故旋轉曲面方程為給定yoz

面上曲線M(

x,

y,

z)x2z

z

,

y2

y1

1C若:點

M

(0,

y

,

z

)

C,

則有1

1

1f

(

y1

,

z1

)

0當繞z

軸旋轉時,該點轉到M

(x,y,z),則有x2f

(

y2

,

z)

0f

(

y,

z)

0ozxCM1

(0,

y1

,

z1

)上機動頁下頁返回結束C

:

f

(

y,

z)

0oyz當曲線C

繞y

軸旋轉一周的旋轉曲面方程為x2f

(

y

,

z2

)

0xxOz

坐標面上的已知曲線f

(x,z)

0繞x

軸旋轉一周的旋轉曲面方程為上機動頁下頁返回結束y2f

(

x,

z2

)

0解x2z

y2

cotyOz面上直線方程為z

y

cot圓錐面方程例2直線L繞另一條與L相交的直線旋轉一周所得旋轉曲面稱為圓錐面.兩直線的交點稱為圓錐面的頂點,兩直線的夾角(0

)稱為2圓錐面的半頂角.試建立頂點在坐標原點O,旋轉軸為z軸,半頂角為

的圓錐面的方程.yxzOxyzO上機動頁下頁返回結束圓錐面的方程也可寫成圓錐面的幾種常用形式z

x2

y2與x2z

1

y2

,

z

2(

x2

y2

)分別表示開口朝上與朝下的半錐面.(a

cot

0)z2

a2

(

x2

y2

)上機動頁下頁返回結束xyx2a2

c2

y2

z2

1繞z

軸旋轉所成曲面方程為

z2a2x2

y2

1c2這兩種曲面都叫做旋轉雙曲面.軸和z

軸旋轉一周所生成的旋轉曲面方程.解:繞x

軸旋轉所成曲面方程為x2

z2上機動頁下頁返回結束a2

c2例3.

求坐標面

xoz

上的雙曲線

1

分別繞

xxyz三、柱面引例.分析方程表示怎樣的曲面.圓x2

y2

R2表示圓柱面oClMM1解:在xoy

面上，x2

y2

R2

表示圓C,1在圓C上任取一點

M

(

x,

y,0),

過此點作平行z

軸的直線

l,對任意

z

,點M

(x,y,z)的坐沿標曲也線滿C平足行方于程zx軸2

的y一2

切R直2

線所形成的曲面稱為柱面.其上所有點的坐標都滿足此方程,故在空間x2上機動頁下頁返回結束

y2

R2xyzxyzo表示拋物柱面,母線平行于

z

軸;準線為xoy

面上的拋物線.

1表示母線平行于z

軸的橢圓柱面.定義

平行定直線并沿定曲線

C

移動的直線

l

形成的軌跡叫做柱面.

C叫做準線,

l

叫做母線.x2

y2

b2a2x

y

0

表示母線平行于z軸的平面.(且z

軸在平面上)Cxyzoo上機動頁下頁返回結束xl2一般地,在三方程G(y,z)

0

表示柱面,母線平行于x

軸;準線yoz

面上的曲線l2.方程H

(z,x)

0

表示柱面,母線平行于

y

軸;準線xoz

面上的曲線l3.母線平行于z軸;準線xoy

面上的曲線

l方程F

(x,y)

0

表示柱面,1.xzl3xyl1上機動頁下頁返回結束四、二次曲面三元二次方程Ax2

By2

Cz2

Dxy

Eyx

FzxGx

Hy

Iz

J

0(二次項系數不全為

0)的圖形通常為二次曲面.其基本類型有:橢球面、拋物面、雙曲面、錐面適當選取直角坐標系可得它們的標準方程,下面僅就幾種常見

的特點進行介紹.研究二次曲面特性的基本方法:截痕法上機動頁下頁返回結束1.橢球面范圍：x

a,

y

b,

z

c與坐標面的交線：橢圓

1

,2

b2z

0

a2

c2

x2

y2

y2

z2

1

,x

0

b

x2

z2

12

c2y

0

ax2

y2

z2a2

b2

c2上機動頁下頁返回結束

1（a,b,c為正數）x2

y2

z2a2

b2

c2

1(3)

截痕:與z

z1

(z1

c)的交線為橢圓：同樣也為橢圓.(4)

當

a＝b

時為旋轉橢球面;

當a＝b＝c

時為球面.x2y21c2z

z1a2

(c2

z

2

)1c2b2

(c2

z

2

)

1(a,b,c為正數)y

y1

(

y1

b

)

及

x

x1（

x1

a）的截痕上機動頁下頁返回結束x22.

拋物面(1)

橢圓拋物面2y2

p

2q

z(p,q

同號)zxyoz上機動頁下頁返回結束oyxp

0,

q

0p

0,

q

0特殊地:

當

p

q

時,

方程變為

z

旋轉拋物面2

p

2

p2yx2z

1

x2

y2分別表示開口朝上與朝下的旋轉拋物面.例如z

2

x2

y2與xyzOp

q

02

p

2qy22x

z

(p

與q

同號)設

p

0,

q

0xy圖形如下：zO(2)

雙曲拋物面(馬鞍面)3.

雙曲面(1)單葉雙曲面xx2

y