專題08勾股定理與翻折

內容早知道

》第一層鞏固提升練（7大題型）

題型一矩形翻折之折痕過對角線

題型二矩形翻折之折痕過一個頂點

題型三矩形翻折之折痕過邊上任意兩點

題型四三角形翻折之過一個頂點所在直線（落點在一邊上）

題型五三角形翻折之過斜邊中點所在直線

題型六三角形翻折之過任意兩點所在直線（落在其中一邊）

題型七三角形中的其他翻折問題

臺第二層能力培優(yōu)練

臺第三層拓展突破練

-------------------------------------------------------------

題型一矩形翻折之折痕過對角線

☆技巧積累與運用

矩形翻折之折痕過對角線模型：如圖，沿著矩形的對角線所在直線進行翻折.

條件：已知矩形48co中，以對角線/C為折痕，折疊A/2C,點2的對應點為2’.

結論：①AABCw"B'C;②折痕/C垂直平方8"；③A/EC是等腰三角形.

（23-24八年級上?河南南陽?期末）

1.如圖，在長方形N8CD中，4B=3cm,3C=4cm.將長方形沿對角線NC折疊，點。落在

了D位置,4。與2c相交于點E.貝!JBE的長等于（）

試卷第1頁，共16頁

25

C.—cmD.-cm

36

（23-24八年級下?山東濟寧?階段練習）

2.如圖，在平面直角坐標系中，四邊形048C為矩形（長方形），。/=6,OC=8,將ZUBC

沿對角線NC翻折，使點8落在點夕處，48'與了軸交于點。，求點。的坐標.

題型二矩形翻折之折痕過一個頂點

☆技巧積累與運用

沿著矩形的一個頂點和一邊上的點的線段所在直線進行翻折.

條件：己知矩形48CD中，以NE為折痕，點5的對應點為2’.

結論：①如圖1,折在矩形內，①三②折痕/C垂直平方8".

②如圖2,折在矩形邊上，①"BE三MB'E;②折痕/C垂直平方班

③如圖3,折在矩形外，①四邊形三四邊形/月CZ'；②折痕NC垂直平方28'；③△

/￡尸是等腰A.

（23-24八年級上?四川成都?期末）

3.如圖，長方形紙片/BCD中，已知40=8,折疊紙片使A8邊與對角線/C重合，點2

落在點尸處，折痕為且8E=3.

試卷第2頁，共16頁

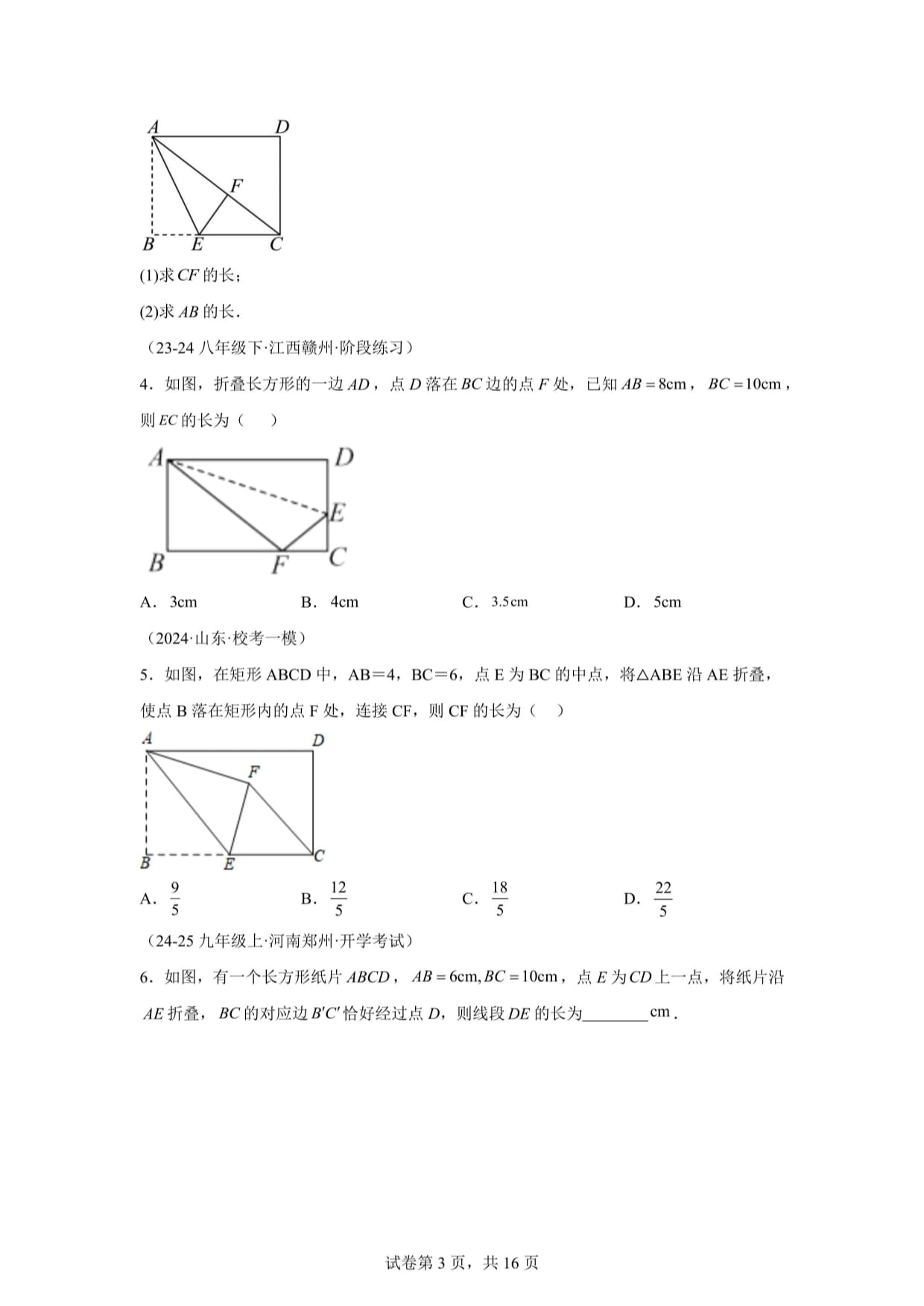
⑴求CF的長；

（2）求的長.

（23-24八年級下?江西贛州?階段練習）

4.如圖，折疊長方形的一邊/。，點。落在8C邊的點尸處，已知NB=8cm,fiC=10cm,

A.3cmB.4cmC.3.5cmD.5cm

（2024?山東?校考一模）

5.如圖，在矩形ABCD中，AB=4,BC=6,點E為BC的中點，將4ABE沿AE折疊,

使點B落在矩形內的點F處，連接CF,則CF的長為（）

（24-25九年級上?河南鄭州?開學考試）

6.如圖，有一個長方形紙片48CD,48=6cm,8c=10cm,點￡為上一點，將紙片沿

NE折疊，5c的對應邊"C恰好經(jīng)過點D,則線段。E的長為cm.

試卷第3頁，共16頁

B'

（2023秋?江蘇?九年級專題練習）

7.如圖所示，在長方形/BCD中，AB=26,在線段8c上取一點E,連接/￡、ED,將

△4BE沿/E翻折，點8落在點夕處，線段E9交/。于點尸.將AECD沿。E翻折，點C

的對應C'恰好落在線段EV上，且點C'為m，的中點，則線段即的長為（）

A.3B.273C.4D.372

題型三矩形翻折之折痕過邊上任意兩點

☆技巧積累與運用

沿著矩形邊上的任意兩點所在直線進行翻折.

條件：已知矩形48C。中，以￡,尸為折痕，點8的對應點為夕，點。的對應點為C’.

結論：如圖1,折在矩形內，①ABEFEAB'EF;②折痕￡尸垂直平方88’.

如圖2,折在矩形邊上，①四邊形班C廠三四邊形ERCR'；②折痕斯垂直平方22’.

如圖3,折在矩形外，①四邊形理CF三四邊形￡力0k；②折痕/C垂直平方瓦?’；③△

GCF是RtA.

例

（2023?駐馬店?八年級校考期中）

試卷第4頁，共16頁

8.如圖，在長方形紙片中，，28=10,8c=12,點￡是42的中點，點F是AD邊

上的一個動點，將A4E尸沿斯所在直線翻折，得到尸，連接/C,/。，則當A4Z）尸是

直角三角形時，/力的長是.

例

（23-24八年級下?安徽蚌埠?期中）

9.如圖，長方形紙片/8C。中，AB=3cm,AD=9cm,將此長方形紙片折疊，使點。、B

重合，點C落在點X的位置，折痕為EF,貝的面積為（）

A.5cm2B.6cm2C.8cm2D.10cm2

例

（23-24八年級上?遼寧沈陽?期中）

10.如圖，正方形的邊長為4,點￡,尸分別在邊NO,8C上，將四邊形/皮近沿訪

折疊得到四邊形EFMW,點/的對應點M恰好落在直線上.若。初=1,則線段8尸的長

題型四三角形翻折之過一個頂點所在直線（落點在一邊上）

★技巧積累與運用

試卷第5頁，共16頁

1）沿過點A的直線翻折使得點B的對應點為8’落在斜邊AC上，折痕為AD；

2）沿過點C的直線翻折使得點2的對應點為5’落在斜邊NC上，折痕為CD；

3）沿過點B的直線翻折使得點A的對應點為E落在BC邊上，折痕為BD.

（23-24八年級下?湖北十堰?階段練習）

11.如圖，有一塊的紙片，ZABC=90°,AB=6,5C=8,將△ASC沿4D折疊,

使點3落在NC上的E處，連接ED,則5D的長為（）

A.3B.4C.5D.6.

（23-24八年級下?湖南岳陽?開學考試）

12.如圖所示，有一塊直角三角形紙片，ZC=90°,SC=6cm,^5=10cm,將斜邊AB翻

折，使點2落在直角邊NC的延長線上的點￡處，折痕為則CE的長為（）

E

A.2cmB.3cmC.4cmD.5cm

（23-24八年級上?江蘇常州?期末）

13.如圖，在RtZ\/8C中，ZACB=90°,AC=6,BC=8,點。在斜邊42上，將

沿CD折疊，使點A恰好落在邊上的點E處，則△ADE的周長為.

試卷第6頁，共16頁

題型五三角形翻折之過斜邊中點所在直線

*技巧積累與運用

1）沿直線（N為斜邊中點）翻折使得點/與點C重合；

2）沿中線5E翻折，使得點/落在點尸處，連結/RFC,4F與BE交于點、O.

3）沿中線翻折，使得點C落在點。處，連結AD,CD.

（23-24八年級上?四川成都?階段練習）

14.如圖，是一張紙片，ZC=90°,AC=6,BC=8,現(xiàn)將其折疊，點B與點A重合,

折痕為DE,則2。的長為（）

C

（2023春?廣西?八年級專題練習）

15.已知，如圖，在44BC中，NC=90。,/8=10,NC=6,a）是/JB上的中線，如果將A5CD

沿8翻折后，點3的對應點〃，那么的長為.

（23-24八年級下?遼寧葫蘆島?階段練習）

試卷第7頁，共16頁

16.已知必A48C中，/C=90°,NC=8,5C=4,D為斜邊的中點.E是直角邊NC上的

一點，連接DE,將沿。E折疊至△4DE/E交2D于點尸，若SEF的面積是

A.2B.3C.2亞D.2g

題型六三角形翻折之過任意兩點所在直線（落在其中一邊）

★技巧積累與運用

1）沿直線翻折，使得點C落在直角邊的點D處，連結CD；

2）沿直線DE翻折使得點C與斜邊上的點/重合.

（23-24八年級下?廣東中山?期中）

17.如圖，在RtZ\/BC中，ZC=90°,AC=6,BC=8,將它的銳角A翻折，使得點A落

在邊8c的中點。處，折痕交NC邊于點E,交48邊于點尸，則DE的長為（）

13

A.3B.4C.—D.

3

例

（23-24八年級上?重慶?階段練習）

試卷第8頁，共16頁

18.如圖，在△/8C中，ZC=90°,AC=BC=5,點瓦尸分別為邊與8c上兩點，連接

EF,將即沿著E尸翻折，使得5點落在NC邊上的。處，AD=2,則CF的值為.

（2022?重慶市七年級期中）

19.如圖，在△NBC中，^LACB=90°,點、D,E分別在邊/C、8c上，且乙CDE=￡B,將△口?￡

沿DE折疊，點C恰好落在AB邊上的尸點，若CD=4,CE=3,DE=5,則AB的長為.

題型七三角形中的其他翻折問題

例

（23-24八年級上?江蘇揚州?期中）

20.如圖，三角形紙片中，點。是8C邊上一點，連接力D,把沿著直線翻

折得到AAED,DE交/C于點G,連接BE交AD于點F,若DG=EG,AF=4,AB=5,LAEG

例

（2023?重慶?八年級統(tǒng)考期末）

試卷第9頁，共16頁

21.如圖，在RtZ\48C中，ZC=90°,ZA=30°,2C=6,點。在邊/C上，將沿

直線8。翻折后，點/落在點E處.如果4D_L￡。，那么線段。E的長為

例

（2023秋?江蘇?八年級專題練習）

22.如圖，在中，ZC=90°,AC=6,8C=8,點尸在/C上，并且CF=2,點￡

為BC上的動點（點E不與點C重合），將ACE尸沿直線所翻折，使點C落在點尸處，PE

的長為，則邊斯的長為（）

8

A.-B.3D.4

3

例

（2023?吉林?三模）

23.如圖，在△N8C中，ZACB=90°,點。、尸為邊48上的點，連接。、CF,將△BCD

沿8翻折，使點3的對稱點落在邊N8上的點E處；再將尸沿CF翻折，使點A的對

稱點落在CE的延長線上的點H處.若NC=8,/8=10,則斯的長為.

試卷第10頁，共16頁

li

（2024?四川廣安?二模）

24.如圖，有一張長方形片/BCD,AB=8cm,8C=10cm.點E為CD上一點，將紙片沿

4&折疊，8c的對應邊"C恰好經(jīng)過點。，則線段DE的長為（）cm

（23-24八年級上?江蘇鹽城?期末）

25.如圖所示，有一塊直角三角形紙片，ZACB=90°,AC^4,BC=3,將斜邊N2翻折，使點5

落在直角邊NC延長線上的點E處，折痕為則CE的長為（）

45

A.1B.-C.1.5D.一

33

（23-24八年級下?湖北荊州?階段練習）

26.如圖，中，ZC=90°,BC=2,/C=3,將沿DE翻折，使點A與點

B重合，則NE的長為（）

試卷第11頁，共16頁

（2024?山東濱州?三模）

27.如圖，在Rta/BC中，Z5=9O°,AB=9,BC=6.將△NBC折疊，使點A落在BC

的中點。處，折痕為"N,則線段ON的長為（）

（2023春?湖北黃石?八年級統(tǒng)考階段練習）

28.如圖，把矩形/BCD沿防翻折，點3恰好落在/。邊的9處，若/E=l,DE=3,

NEFB=60°,則矩形ABCD的面積是.

BFC

（2023秋?四川雅安?八年級統(tǒng)考期末）

29.在Rta/CB中，N4CS=90。，點。在邊N8上，連接8,將△/DC沿直線翻折,

點/恰好落在2C邊上的點￡處，若NC=6,BE=2,則。E的長是.

試卷第12頁，共16頁

（2023秋?江蘇?八年級專題練習）

30.如圖，AD是A48C的中線，/4DC=30。，把△NOC沿著直線/。翻折，點C落在點E

的位置，如果3c=4,那么線段BE的長度為一.

（23-24九年級上?重慶九龍坡?期中）

31.如圖，在△/8C中，ZC=90°,AC=BC=6,點、E,尸分別為邊NC,N2上的點，連接

EF，將AAEF沿著EF翻折,使得A點落在BC邊上的。處，8。=4,則。尸的長度為.

（2024?遼寧?模擬預測）

32.如圖，將△NBC沿直線/C翻折得到△/OC,BD交AC于點、E,尸為CO的中點，連

接力尸并延長，交8c的延長線于點G,連接斯，若/8=10,AE=6,△/￡）尸的面積為

18,則的面積為.

33.如圖，在矩形/BCD中，4B=8,BC=4,將矩形沿對角線NC折疊，點。落在力處.

試卷第13頁，共16頁

DC

⑴求CN的長；

（2）求重疊部分A4FC的面積.

-------------------------------------------------------------------------

（2023春?湖北?八年級專題練習）

34.如圖，在"BC中，點。是邊上的中點，連接CD,將ABCD沿著CD翻折,得至I]AECD,

CE與4B交于點、F,連接若4B=6,CD=4,AE=2,則點C到48的距離為（）

E

B---------------------C

A.1B.472C.延D.2A/2

23

（22-23九年級下?福建南平?自主招生）

35.如圖，中，ZACB=90°,AC=6,BC=8,將邊NC沿CE翻折，使點

A落在上的點。處；再將邊沿CF翻折，使點3落在8的延長線上的點夕處，兩

條折痕與斜邊分別交于點￡、F,則線段。廠的長為（）

試卷第14頁，共16頁

A.V3B.72

（2023?山東淄博?七年級期中）

36.如圖，在四邊形中，44=90。，4B=4cm,AD=2cm,BC=CD,E是上

的一點.若沿CE折疊，使8,。兩點重合，則△/￡￡＞的面積為____.

（2024?內蒙古?八年級期末）

37.如圖在三角形紙片45C中，已知//8C=90。，4C=5,BC=4,過點/作直線/平行

于3C,折疊三角形紙片4BC,使直角頂點8落在直線/上的點P處，折痕為MN,當點尸

在直線/上移動時，折痕的端點M、N也隨之移動，若限定端點M、N分別在N8、/C邊上

移動，則線段/尸長度的最小值為.

（2023?江西撫州?八年級統(tǒng)考期中）

38.如圖，在矩形ABCD中，AB=8,8C=10,點尸在矩形的邊CO上由點。向點C運動.

沿直線/尸翻折形成如下四種情形，設。P=x,A4OP和矩形重疊部分（陰影）的

面積為

A...............J）A...........0&..........、D%................Q

（1）如圖4,當點尸運動到與點C重合時，求重疊部分的面積了；

（2）如圖2,當點尸運動到何處時，翻折AAD尸后，點。恰好落在邊上？這時重疊部分

的面積了等于多少？

（2023?廣東深圳?八年級校考期中）

試卷第15頁，共16頁

39.如圖所示，在矩形ABCD中，AB=CD=5,BC=AD=3.

圖①圖②圖③

⑴如圖①，E、F分別為CD、AB邊上的點，將矩形ABCD沿EF翻折，使點A與點C重

合，設CE=x,則DE=_(用含x的代數(shù)式表示)，CD，=AD=3,在RdCDE中，利用勾股定理

列方程，可求得CE=_.

(2)如圖②，將4ABD沿BD翻折至aABD,若A，B交CD于點E,求此時CE的長；

(3)如圖③，P為AD邊上的一點，將4ABP沿BP翻折至AABP,A，B、AT分別交CD邊

于E.F,且DF=A，F(xiàn),請直接寫出此時CE的長.

(2023?江蘇蘇州?八年級期末)

40.(1)如圖1,將矩形ABCD折疊，使BC落在對角線BD上，折痕為BE,點C落在點C，

處，若NADB=46°,貝ijNDBE的度數(shù)為°.

(2)小明手中有一張矩形紙片ABCD,AB=4,AD=9.

【畫一畫】

如圖2,點E在這張矩形紙片的邊AD上，將紙片折疊，使AB落在CE所在直線上，折痕

設為MN(點M,N分別在邊AD,BC上)，利用直尺和圓規(guī)畫出折痕MN(不寫作法，保留

作圖痕跡，并用黑色水筆把線段描清楚)；

【算一算】

如圖3,點F在這張矩形紙片的邊BC上，將紙片折疊，使FB落在射線FD上，折痕為

7

GF,點A,B分別落在點A，，B，處，若AG=],求BD的長；

試卷第16頁，共16頁

1.A

【分析】本題主要考查了圖形的折疊問題，勾股定理.設成=xcm,則EC=（4-x）cm,

根據(jù)題意可證得A/BE0ACE。'，可得BE=ED=xcm.在Rt^CE。'中，根據(jù)勾股定理可

得到關于x的方程，求解即可得到答案.

【詳解】解：設3￡=xcm,則EC=（4-x）cm.

根據(jù)圖形折疊的性質得：CD=CD',AD=AD'.

???四邊形/BCD為長方形，

...AB=CD=3cm,ZB=ZD=90°.

...AB=CD'=3cm,NB=ND'=90°.

在ANBE和ACEZ）'中

vZB=ZD',ZAEB=ZCED',AB=CD',

：."BE絲ACW（AAS）.

BE=ED'=xcm.

在RtZ^CED'中，EC2=ED'1+CD'1

即（4一才=X?+32.

7

解得：x=w.

o

7

BE=—cm.

8

故選：A.

2.Z）的坐標為

【分析】根據(jù)題意由折疊的性質可知，/B，AC=/BAC,NBAC=NDCA,易得DC=DA,設

O0=x,則。C=8-x,在此△40。中，由勾股定理得0。，進一步求得。的坐標，并且主要

考查了翻折變換的性質及勾股定理的應用問題，靈活運用有關定理來分析、判斷、推理或解

答是解題的關鍵.

【詳解】解：由折疊的性質可知=

???四邊形。45。為矩形，

OC\\AB,

??.ABAC=ZDCA,

答案第1頁，共33頁

；"B'AC=ZDCA,

AD=CD,

設OD=x,則。C=8-x,

在氏公/O。中，由勾股定理得，

OA2+OD2=AD2,

即62+X2=(8-X)2,

7

解得：

4

???點D的坐標為：(“一j

3.(1)CF=4

(2)AB=6

【分析】本題考查勾股定理與折疊問題，掌握折疊的性質，利用勾股定理進行求解，是解題

的關鍵.

(1)根據(jù)折疊的性質，得到8￡=防,4尸￡=々=90。，進而得到NEFC=90。，利用勾股

定理進行求解即可；

(2)根據(jù)折疊的性質，得到=4尸，設48=4F=x,在RtZUBC中，利用勾股定理進

行求解即可.

【詳解】(1)解：?.?長方形紙片中，40=8,折疊紙片使A8邊與對角線/C重合，

...BE=EF=3,ZAFE=NB=90°,BC=AD=8,

^EFC=90°,CE=BC-BE=5,

■■CF=yJCE2-EF2=4;

(2)?.?折疊，

*'?AB=AF,

^AB=AF=x,則：AC=AF+CF=x+4,

在RtzX/BC中，AC2=AB2+BC2,

.-.(x+4)2=X2+82,

x—6,

AB—6.

4.A

答案第2頁，共33頁

【分析】此題考查了長方形的性質、勾股定理、折疊的性質等知識，利用勾股定理列方程是

解題的關鍵.四邊形48。?是長方形，則A8=CO=8cm,AD=BC=10cm,

/ABC=NBCD=NADC=90°,由折疊的性質可知/斤=/。=10cm,DE=FE,

CE=CD-DE=S-DE,由勾股定理得到BT7=6cm,則Cb=8C-8F=4cm,

在RtZ\C跖中，由勾股定理得到。尸+0片=跖2,解方程即可.

【詳解】解：???四邊形是長方形，

=CD=8cm,NO=8C=10cm,NABC=4BCD=NADC=90°,

???折疊長方形的一邊NO,點。落在BC邊的點尸處，

.?.4F=4D=10cm,DE=FE,CE=CD-DE=8—DE,

BF=y]AF2-AB2=7102-82=6（cm）,

CF=BC-BF=4cm,

在RtZ\CE尸中，由勾股定理得到。>+。￡2=砂2,

BP42+（8-Z）E）2=￡>￡,2,

解得。￡=5

:.CE=CD-DE=3cm

故選：A.

5.C

【分析】連接BF,（見詳解圖），由翻折變換可知，BF1AE,BE=EF,由點E是BC的中點，

可知BE=3,根據(jù)勾股定理即可求得AE;根據(jù)三角形的面積公式；xABxBE=；x4ExAf/可求

得BH,進而可得到BF的長度；結合題意可知FE=BE=EC,進而可得NBFC=90。，至此，

在RtABFC中，利用勾股定理求出CF的長度即可

【詳解】如圖，連接BF.

?■?AAEF是由4ABE沿AE折疊得到的，

???BF1AE,BE=EF.

.BC=6,點E為BC的中點，

??.BE=EC=EF=3

根據(jù)勾股定理有AE2=AB2+BE2

代入數(shù)據(jù)求得AE=5

答案第3頁，共33頁

根據(jù)三角形的面積公式;x43xBE=；x4Ex8H

得BH=—

5

24

即可得BF=y

由FE=BE=EC,

可得NBFC=90°

再由勾股定理有BC2-BF2=CF2

1O

代入數(shù)據(jù)求得CF=y

1Q

故答案為：—

【點睛】此題考查矩形的性質和折疊問題，解題關鍵在于利用好折疊的性質，對應點的連線

被折痕垂直平分.

6.

33

【分析】本題考查了折疊的性質，勾股定理.

根據(jù)折疊的性質可得=AB'=6cm,CE=C'E,B'C=CB=10cm,Z5=N8=90°,然后在

中，由勾股定理求出HZ）的長，則可得出CZ）的長，再在RtAECD利用勾股定理

進行計算即可求。E的長.

【詳解】解：???四邊形是長方形，

AD=BC=10cm,CD=AB=6cm,Z.B=ZC=90°,

根據(jù)折疊的性質，得4B=4B'=6cm,=CE,B'C'=CB=10cm,AB=/B'=90°,

在RtA4B'￡>中，由勾股定理，得B'D=JAD。-AB'?=8cm，

CD=10-8=2cm,

在RtAECD中,GE?+CD2=DE2,

■\6-DE）2+22=DE2,

答案第4頁，共33頁

解得=

故答案是：—

7.A

【分析】由折疊的性質可得/5=/"=CD=C'D=20,乙B=乙B'=90°=乙C=￡DC'E,

BE=B'E,CE=C'E,由中點性質可得"E=2C'￡,可得BC=4D=3EC,由勾股定理可求

CE的長，由“N4r可證絲△OC戶，可得CF=BR=1,即可求解.

【詳解】解：???四邊形N8CD是矩形，

；.AB=CD=2O,AD=BC,z5=zC=90°

由折疊的性質可得：

AB=AB'=CD=CD=2逝，

乙B=AB'=90°=乙C=Z.DC'E,

BE=B'E，CE=C'E,

乙BEA=4B'EA^-NBEB',(CED=4C'ED=YZCEC

22

；.UED=-ZBEB'+gZCEC

22

=^(ZBEB'+ZCEC)

=-xl80°=90°

2

.?.△/E。是直角三角形

：.AD2=AE2+DE2,

???點C'恰好為班’的中點，

；.B'E=2CE,

：.BE=2CE,

:.BC=AD=3EC,

■：AE2^AB-+BE2,DE2^DC2+CE2,

：.(3CE)2=AB2+BE2+DC2+CE2

即9C￡2=8+4C￡2+8+C￡2,

:.CE=2,

答案第5頁，共33頁

-'-BE—BE—A,BC—AD—6,CE—2,

：.B'C=2,

??ZB'=^DCF=90°,乙4FB'—DFC,AB'^C'D,

.MAB'F沿ADC'F(AAS),

：.C'F=B'F=\,

:.EF=CE+C'F=3,

故選：A.

【點睛】此題考查了翻折變換、矩形的性質、全等三角形的性質、勾股定理等，解題的關鍵

是求出CE的長.

c26f

8.—或7

【分析】根據(jù)題意，分/工4'。=90。及乙4'￡0=90。兩種情況進行討論求解.其中，當

/"'。=90。時，E,A',。三點共線，由矩形性質及已知條件，^AD=BC=U,

4E=5,在及AE/D中，運用勾股定理求得ED的長，再根據(jù)翻折性質，在比△見，￡>中，

運用勾股定理求得ED的長；當乙47加=90。，運用翻折性質，證得是等腰直角三角

形，再運用矩形性質，求得陽的長.

【詳解】解：分兩種情況進行討論，

①當/"'￡>=90。時，

?.?矩形/8C7)中，AAE■尸沿E尸所在直線翻折，得到氏4，百，

ZFA'E=ZA=90°,

..E,A',。三點共線.

?.?矩形/BCD,BC=U,

,-.AD^BC=n.

???48=10,點E是月8的中點，

AE=5.

.,.在R/AEAD中，

ED=sjAE2+AD2=VF+1F=13.

???AAE?尸沿E尸所在直線翻折，得到大4，￡7"AE=5,

A'E=AE=5,

；.A'D=ED-A'E=13-5=8.

答案第6頁，共33頁

設ArF=x,

則AF=AfF=x,

???4F+FD=4D=12,

FD=12-x,

???NE4'D=90。,

???在放中，

A'F2+A'D2=FD2,BPx2+82=(12-x)2,

解得，x=g

.-.FD=AD-AF^12--=—.

33

②當N4NZ)=90。時，

-ZAFD=1SO°,

??.NAFA'=ZAFD-ZArFD=90°.

??.\AEF沿EF所在直線翻折，得到\ArEF,

ZAFE=ZEFAf=-ZAFAr=45°.

2

?.?矩形/BCD,

???44二90。.

-ZAFE=45°,

:.LEAF是等腰直角三角形.

???45=10,點石是45的中點，

AE=AF=-AB=5,

2

?.?矩形/BCD,BC=n,

AD=BC=n,

：,FD=AD-AF=12-5=7.

綜上所述，ED的長為m或7.

【點睛】本題考查了矩形的翻折問題，熟練運用翻折性質、勾股定理，是解題的關鍵.

9.B

【分析】設NE=XC〃7,則￡D=8E=9-X(c加)，根據(jù)勾股定理可求得的長，從而

答案第7頁，共33頁

不難求得的面積，本題考查了利用勾股定理解直角三角形的能力.

【詳解】

解：設=由折疊可知：ED=BE=9-x^cm),

??,在RtZ\/8￡1中，32+x2=(9-x)2

二.x=4,

..S=—AEAB=—x3x4=6(cm2)

△ADRLF22\/

故選：B.

【分析】當點M在邊40上時，連結NM,過點尸作陽于點“，證明會"DM’

得到HE=DM=1,然后根據(jù)勾股定理列方程。爐+12=(4-叫2,解得。￡弋，即可進一

O

步求得答案；點M在邊CD的延長線上時，連結NM,交巫的延長線于點K,過點尸作

也于點心同理求得也=1,。￡=岸，即可進一步求得另一個答案.

O

【詳解】解：如圖1,點M在邊4。上時，連結過點尸作方HLZD于點”，

丁四邊形ABFE沿EF折疊得到四邊形EFNM,

:.EFLAM,AE=ME,

???四邊形/BCD是正方形，

:.ZD=90°,AB=AD,

:.ZFHE=ZD=90°,

vZFEH+ZDAM=90°fZAMD+ADAM=90°,

AFEH=/AMD,

???/BAH=ZABF=ZFHA=90°,

???四邊形/BF〃時矩形，

AB=FH,

FH=AD,

:.^FHE^ADM(\AS),

：.HE=DM=\,

在RMOEM中，ME=4—DE,

:.DE2+DM2=ME2，

答案第8頁，共33頁

DE2+『=(4-DE)2,

解得OE弋

O

-V7

179

...AH=AE-HE=——1=-

88

圖1

如圖2,點M在邊CD的延長線上時，連結交代的延長線于點K,過點尸作尸2,

于點L,

同理可得也=ZQ,ZFLE=ZADM=90°,

ZFLE=ZAKE=90°,/FEL=/AEK,

ZEFL=ZMAD,

.?.△在7星“MD(ASA),

LE=DM=1,

在RMOEM中，DE2+DM2=ME2,

.-.Z)￡2+12=(4-Z)￡)2,

解得。￡弋

o

■■?^=4-7=T

1725

AL=AE+HL=-----F1=—

88

25

：.BF=AL=—

8

答案第9頁，共33頁

圖2

925

綜上所述，線段8尸的長度為J或胃.

OO

故答案為：9或三25.

OO

【點睛】此題考查了軸對稱的性質，正方形的性質，全等三角形的判定與性質，勾股定理等

知識，正確地分類及作出所需要的輔助線是解題的關鍵.

11.A

【分析】本題考查勾股定理，折疊的性質，解題關鍵在于求得NC的長.由題意可得

NAED=NB=90。,AE=4B=6,由勾股定理即可求得NC的長，則可得EC的長，然后設

BD=ED=x,則CO=2C-&)=8-x,由勾股定理CD?=￡C?+瓦丫，即可得方程，解方

程即可求得答案.

【詳解】解：.??點E是沿/。折疊，點3的對應點，連接ED,

:.NAED=NB=90。，AE=4B=6,

??,在RtZi/BC中，ZB=90°,AB=6,BC=8,

:.AC=yjAB2+BC2=10>

EC=AC-AE=1Q-6=4,

設BD=ED=x,貝lJCZ>=2C-2Z)=8-x,

在RtZ\CDE中,CD2=EC2+ED2,

即：(8-X)2=X2+16,

解得：x=3,

二.BD=3.

故選：A.

12.A

【分析】本題考查了勾股定理及折疊的性質，熟練掌握勾股定理的解本題的關鍵.由勾股定

答案第10頁，共33頁

理可求出NC=8cm,根據(jù)折疊的性質可得出4E=AB=10cm,進而可直接由CE=/E-NC求

解.

【詳解】解：在RtZ\48C中，AC=y/AB2-BC2=8cm>

根據(jù)折疊的性質可知：4E=AB=10cm.

:.CE=AE—AC=2cm.

故選：A.

13.12

【分析】本題考查翻折變換（折疊問題），勾股定理.由折疊可得，AC=CE,DE=AD,

則CE=6,BE=2,再由的周長=ZB+仍，即可求解.

【詳解】解：由折疊可得，AC=CE,DE=AD,

???/C=6,BC=8,

CE=6,

:.BE=BC-CE=2,

-ZACB=90°,

AB=ylAC2+BC2=10，

：.ABDE^j^^z=DE+EB+BD=AD+BD+EB=AB+EB=10+2=12.

故答案為：12.

14.C

【分析】本題考查的是勾股定理的應用，軸對稱的性質，先求解/3=10,設。8=x,可得

CD=8-x,再利用勾股定理求解即可.

【詳解】解：???NC=90O,/C=6,3C=8,

AB-+8。=10，

根據(jù)翻折可得：BD=AD,

設D8=x，根據(jù)圖形翻折可得：/。=x,CD^-x,

在直角三角形工。中，根據(jù)勾股定理可得：62+（8-x『=/,

解得x=f25，

4

4

故選C.

答案第11頁，共33頁

【分析】先用勾股定理求得BC,利用斜邊上的中線性質，求得CD,BD的長，再利用折疊

的性質，引進未知數(shù)，用勾股定理列出兩個等式，聯(lián)立方程組求解即可.

【詳解】如圖所示，

ZACB=90°,AB=10,AC=6,

.-，BC=7102-62=8-

???CD是48上的中線，

???CD=BD=AD=5,

設DE=x,BE=y,

根據(jù)題意，得

x2+y2=25,

(x+5)2+廿=64,

解得x=71,y=2§4,

,48

故答案為：—.

【點睛】本題考查了勾股定理，斜邊上中線的性質，方程組的解法，折疊的性質，熟練掌握

折疊的性質，正確構造方程組計算是解題的關鍵.

16.A

【分析】本題主要考查了折疊問題、勾股定理的運用、全等三角形的判定和性質等知識，折

疊是一種對稱變換，它屬于軸對稱，折疊前后圖形的形狀和大小不變，位置變化，對應邊和

對應角相等.連接5E,過。作DGL/C于G,先判定A/'。尸父尸(SAS),即可得出

答案第12頁，共33頁

A'D=BE=AD=；AB=2小,再根據(jù)勾股定理求得CE的長.

【詳解】解：如圖所示，連接BE,過E作EGL/8于G,

???由勾股定理得AB=ylAC2+BC2=4>/5，

由折疊可得，MDE與，'DE全等,

.ADEF的面積是面積的一半，S“ADE=；AD-EG,S“EDF=；FDEG,

.?.ADE下的面積是A/'OE面積的一半，DF^AD,

2

.?尸是WE的中點，

A'F=EF

又?.?。是48的中點，

.■.DF^AD=\BD=BF,即尸是8。的中點，

22

又：ZA'FD=ZEFB,

；."'DF學AEBF(SAS),

A'D=BE=AD=-AB=2石，

2

又???NC=90°,

RLBCE中，CE=SJBE2-BC2=J20-16=2，

故選：A.

17.D

【分析】本題考查了折疊的性質、勾股定理，由題意得出：。=

8=84,由折疊的性質可

得AE=DE,則CE=6-無，再勾股定理計算即可得出答案.

【詳解】解：.??點。為2C的中點，

答案第13頁，共33頁

:.CD=~BC=4,

2

由折疊的性質可得：AE=DE,

設AE=DE=x,貝！|CE=/C-CE=6-x,

由勾股定理可得：CE2+CD2=DE2,

（6-x）2+42=x2,

13

解得：尤=5，

DE^—,

3

故選：D.

18.1.6

【分析】本題考查的是軸對稱的性質，勾股定理的應用，本題先設CF=x,再表示

BF=DF=5-x,再利用勾股定理建立方程求解即可，熟記勾股定理的含義是解本題的關鍵.

【詳解】解：設CF=x,

vAC=BC=5,AD=2,

:.CD=3,BF=DF=5-x,

vZC=90°,

???（5-x）2=X2+32,

解得：x=1.6,

???C尸=1.6,

故答案為：L6

48

19.——

5

12

【分析】連接CF交加于。，由已知。￡=5,由三角形面積公式可求。。=丁，由折疊的

2474

性質可求CF=w，由等腰三角形的判定可得/尸=CF=B尸=7,即可求的長.

【詳解】解：如圖，連接CF交DE于。，

答案第14頁，共33頁

???將\CDE沿DE折疊，點。恰好落在45上的尸處,

/.OC=OF,CFVDE,

???CD=4,CE=3,AACB=90°,DE=5,

,/S.=—xCDxCE=—xDExCO,

rnP22

24

:.CF=—

5

-ZACB=90°,

:.ZA+ZB=90Q,且/CQE+/4Cb=90。，ZCDE=ZB,

/./Z=ZACF,

24

/.AF=CF=—,

5

24

同理可求：BF=CF=—,

48

/.AB=AF+BF=——，

5

48

故答案為：—.

【點睛】本題考查了翻折變換，等腰三角形的判定，證明/尸=。尸=8尸是本題的關鍵.

20.V10

【分析】本題考查了三角形與折疊問題，勾股定理等知識點.根據(jù)題意推出S“m是解題關

鍵.

【詳解】—G,△3的面積為j

c15

,?°AADG24EG4

,,°4ADE=SRADG+SUEG=

AABD沿著直線4D翻折得到AAED,

答案第15頁，共33頁

==

**,S&ABDLADE§'BF_LAD,

???4尸=4,AB=5,

???BF=yjAB2-AF2=3

VS△?A.BD=2-xADxBF=—2,

AD=5

：.DF=AD-AF=\

22

?1?BD=^JBF+DF=Vio

故答案為：VTo

21.6g-6

【分析】連接NE,根據(jù)翻折的性質可得N48O=NE5D,AD=DE,AB=BE,由ND_LE。

可得△/￡>￡是等腰直角三角形，可求出/以￡=75。，根據(jù)等腰三角形的性質可求出

ZABE=30。,即可求出/48。=15。，由直角三角形兩銳角互余可得N48C=60。，即可求

出/C8O=45。，可證明△BCD是等腰直角三角形，可得CD=5C,根據(jù)含30。角的直角三

角形的性質可得4B=22C,