垂徑定理 市賽獲獎_第1頁
垂徑定理 市賽獲獎_第2頁
垂徑定理 市賽獲獎_第3頁
垂徑定理 市賽獲獎_第4頁
垂徑定理 市賽獲獎_第5頁
已閱讀5頁，還剩5頁未讀， 繼續免費閱讀

下載本文檔

版權說明：本文檔由用戶提供并上傳，收益歸屬內容提供方，若內容存在侵權，請進行舉報或認領

文檔簡介

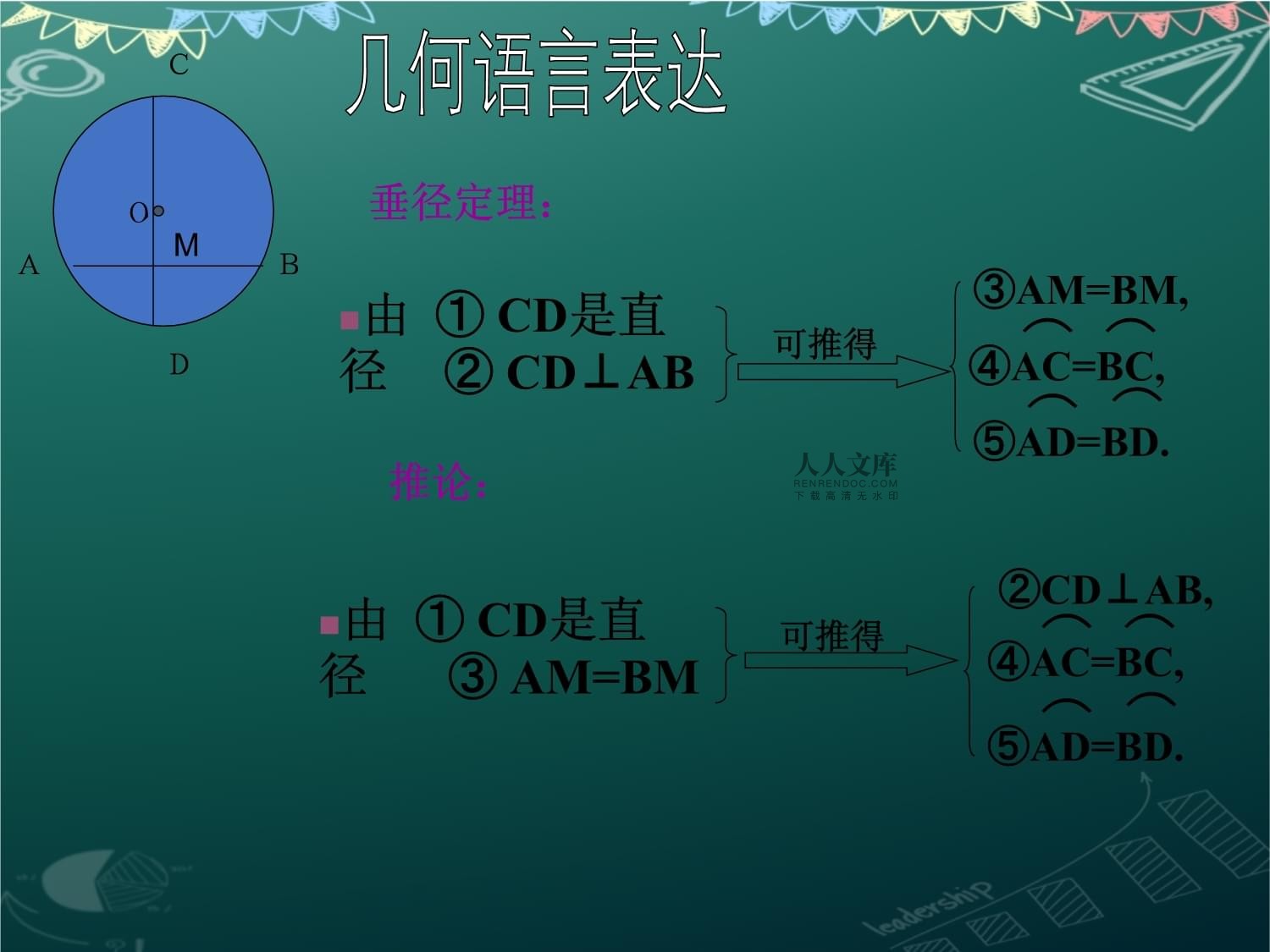
24.1.2垂徑定理第二課時③AM=BM,由①CD是直徑②CD⊥AB可推得⌒⌒⑤AD=BD.⌒⌒④AC=BC,②CD⊥AB,由①CD是直徑③AM=BM⌒⌒④AC=BC,⌒⌒⑤AD=BD.可推得ＤＣＡＢMＯ幾何語言表達垂徑定理：推論：返回退出練習在直徑為650mm的圓柱形油槽內裝入一些油后，截面如圖所示.若油面寬AB=600mm，求油的最大深度.

ED┌

?650600判斷下列說法的正誤①平分弧的直徑必平分弧所對的弦②平分弦的直線必垂直弦③垂直于弦的直徑平分這條弦④平分弦的直徑垂直于這條弦

⑤弦的垂直平分線是圓的直徑⑥平分弦所對的一條弧的直徑必垂直這條弦

⑦在圓中，如果一條直線經過圓心且平分弦，必平分此弦所對的弧辨別是非問題：你知道趙州橋嗎?它是1300多年前我國隋代建造的石拱橋,是我國古代人民勤勞與智慧的結晶．它的主橋是圓弧形,它的跨度(弧所對的弦的長)為37.4m,拱高(弧的中點到弦的距離)為7.2m，你能求出趙洲橋主橋拱的半徑嗎？趙州橋主橋拱的半徑是多少？解得：R≈27．9（m）BODACR解決求趙州橋拱半徑的問題在Rt△OAD中，由勾股定理，得即R2=18.72+（R－7.2）2∴趙州橋的主橋拱半徑約為27.9m.OA2=AD2+OD2AB=37.4，CD=7.2，OD=OC－CD=R－7.2在圖中如圖，用ＡＢ表示主橋拱，設ＡＢ所在圓的圓心為O，半徑為R．經過圓心O作弦AB的垂線OC，D為垂足，OC與AB相交于點D，根據前面的結論，D是AB的中點，C是ＡＢ的中點，CD就是拱高．⌒⌒⌒實踐應用例如圖，某居民區一處圓形水泥管下水管道破裂塌陷，修理人員準備更換一段新管道，現量得污水面寬度為60cm，水到管道頂部距離為10cm，問修理人員應準備內徑是多少的水泥管道？2．如圖，在⊙O中，AB、AC為互相垂直且相等的兩條弦，OD⊥AB于D，OE⊥AC于E，求證四邊形ADOE是正方形．D·OABCE證明：∴四邊形ADOE為矩形，又∵AC=AB∴AE=AD∴四邊形ADOE為正方形.例2

如圖，某菜農在蔬菜基地搭建了一橫截面為圓弧形的蔬菜大棚，大棚的跨度為8米，大棚頂點離地面的高度為2.5米。求該圓弧形所在圓的半徑；若該菜農身高1.75米，則他在不彎腰的情況下，橫向活動的范圍有幾米？ABCDO

解：用AB表示大棚，設AB所在圓的圓心為O，半徑為R.經過圓心O作OC⊥AB于D,交AB于點C，根據垂徑定理，D是AB的中點，C是AB的中點，CD就是大棚高度.

⌒⌒⌒⌒MNE

在Rt△OAD中,由勾股定理得

R2=42+(R－2.5)2解得R=4.45即該圓弧形所在圓的半徑為4.45米.AB=8,AD=AB=4,CD=2.5OD=OC－CD=R－2.512拓展提高退出返回小結1、要把實際問題轉變成一個數學問題來解決.2、熟練地運用垂徑定理及其推論、勾股定理，并用方程的思想來解決問題.3、

溫馨提示

  • 1. 本站所有資源如無特殊說明，都需要本地電腦安裝OFFICE2007和PDF閱讀器。圖紙軟件為CAD,CAXA,PROE,UG,SolidWorks等.壓縮文件請下載最新的WinRAR軟件解壓。
  • 2. 本站的文檔不包含任何第三方提供的附件圖紙等，如果需要附件，請聯系上傳者。文件的所有權益歸上傳用戶所有。
  • 3. 本站RAR壓縮包中若帶圖紙，網頁內容里面會有圖紙預覽，若沒有圖紙預覽就沒有圖紙。
  • 4. 未經權益所有人同意不得將文件中的內容挪作商業或盈利用途。
  • 5. 人人文庫網僅提供信息存儲空間，僅對用戶上傳內容的表現方式做保護處理，對用戶上傳分享的文檔內容本身不做任何修改或編輯，并不能對任何下載內容負責。
  • 6. 下載文件中如有侵權或不適當內容，請與我們聯系，我們立即糾正。
  • 7. 本站不保證下載資源的準確性、安全性和完整性, 同時也不承擔用戶因使用這些下載資源對自己和他人造成任何形式的傷害或損失。

評論

0/150

提交評論