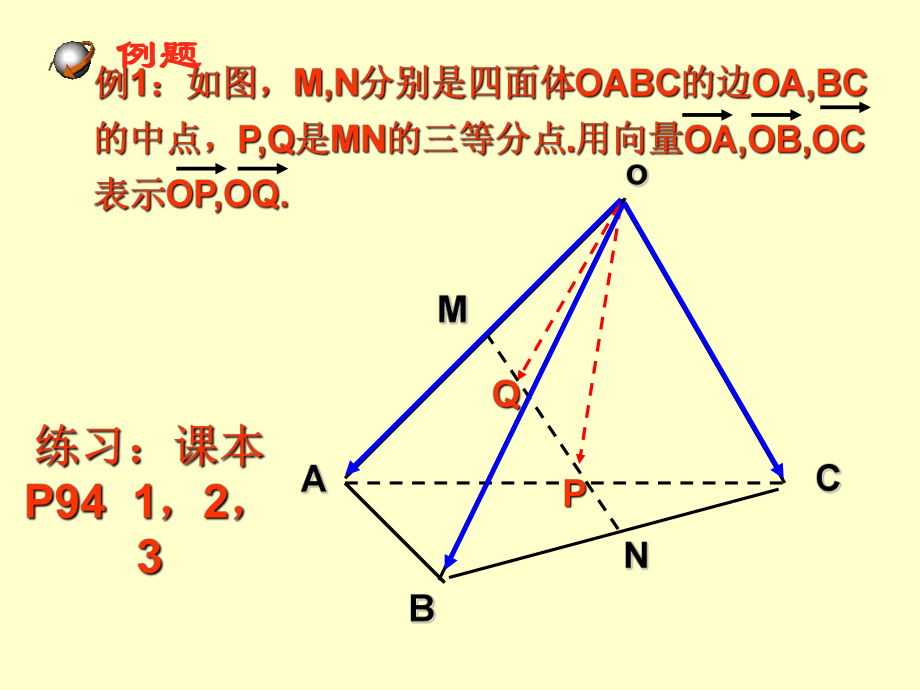
1、3.1.4空間向量的空間向量的正交分解及其坐標表示正交分解及其坐標表示空間向量基本定理空間向量基本定理 如果三個向量如果三個向量a、b、c不共面，不共面，那么對空間任一向量那么對空間任一向量p，存在一個唯一的有序實數組存在一個唯一的有序實數組x，y，z，使使p=xa +yb+zc 定理定理其中其中a，b，c叫做空間的一個基底叫做空間的一個基底.（不共面且非零）（不共面且非零） 建立空間直角坐標系建立空間直角坐標系Oxyz,分別沿分別沿x軸軸,y軸軸,z軸的正方向引單位向量軸的正方向引單位向量e1, e2, e3. 這三個互相垂直的單位向這三個互相垂直的單位向量構成空間向量的一個基底量構成空間向

2、量的一個基底e1, e2, e3這個基底叫做單這個基底叫做單位正交基底位正交基底,單位向量單位向量e1, e2, e3都叫做坐標向量都叫做坐標向量. 空間向量的坐標表示空間向量的坐標表示橫坐標橫坐標x，縱坐標，縱坐標y，豎坐標，豎坐標z .記記p = (x,y,z) 例題例題設設a=(a1，a2，a3)，b=(b1，b2，b3).a+b= (a1 + b1 ， a2 + b2 ，a3+ b3)； a-b= (a1 - b1 ， a2 - b2 ，a3- b3)； a= ( a1 ， a2 ，a3)( 為實數為實數)； ab= a1 b1 + a2 b2 +a3 b3 空間向量的坐標運算空間向量

3、的坐標運算設設A(x1，y1，z1)，B(x2，y2，z2) AB=OB-OA = (x2，y2，z2)-(x1，y1，z1) =( x2 -x1，y2-y1，z2-z1). 一個向量在直角坐標系中的坐標等于表示這個一個向量在直角坐標系中的坐標等于表示這個向量的有向線段的終點的坐標減去起點的坐標向量的有向線段的終點的坐標減去起點的坐標. A(x1，y1，z1)，B(x2，y2，z2)設設M為為AB中點，中點，M點坐標為點坐標為M(x0,yo,zo)其中其中x0=(x1+x2)/2 ；y0=(y1+y2)/2 ；z0=(z1+z2)/2 中點坐標公式中點坐標公式 向量的坐標公式向量的坐標公式ab

4、 a1 a2 a3b1 b2 b3ab (b0)a=b 即即ab (b0)a1=b1,a2=b2, a3=b3,ab=0 共線共線垂直垂直ab a1 b1 + a2 b2 +a3 b3 =0ab 空間向量平行和垂直的條件空間向量平行和垂直的條件例例1. 已知已知a=(1,1,0),b=(0,1,1),c=(1,0,1), p=a-b,q=a+2b-c,求求:p, q, pq.解解:p=a-b =(1,1,0)-(0,1,1)=(1,0,-1);q=a+2b-c =(1,1,0)+2(0,1,1)- (1,0,1)=(0,3,1);pq=(1,0,-1)(0,3,1) =10+03+(-1)1=

5、-1 例題例題|,cosbababa 2322212|aaaaaa 2322212|bbbbbb ;232221232221332211bbbaaabababa ;332211babababa 設設a=(a1，a2，a3)，b=(b1，b2，b3). 兩個向量夾角與向量長度的坐標計算公式兩個向量夾角與向量長度的坐標計算公式;)z(z)y(y)x(xABAB|AB|),z ,y,B(x),z ,y,A(x212212212222111 則則已已知知 空間兩點間的距離公式空間兩點間的距離公式例例2.已知已知A(3,3,1)，B(1,0,5)求：求：線段線段 AB的中點坐標和長度；的中點坐標和長度；

6、zxyoA(3,3,1)B(1,0,5)M設設M(x,y,z)是是AB的中點，那么的中點，那么OM= (OA+OB)21 29153031222, BAd 例題例題例例3:在正方體在正方體ABCD-A1B1C1D1中中,B1E1=D1F1= 求求BE1與與DF1所成的角的余弦值所成的角的余弦值.411BAABCDA1B1C1D1E1F1XYZ解析：不妨設正方解析：不妨設正方體的棱長為體的棱長為1；以；以D為原點為原點O建立空間直建立空間直角坐標系角坐標系O-xyz.OB(1，1，0）)1,43, 1(E1D(0，0，0）F10， ，1）41 例題例題例例4:如圖，在正方體如圖，在正方體ABCD-A1B1C1D1中中,E, F分別是分別是BB1,D1B1的中點，求證：的中點，求證：EFDA1.ABCDA1B1C1D1EFXYZ解析：不妨設正方解析：不妨設正方體的棱長為體的棱長為1；以；以D為原點為原點O建立空間直建立空間直角坐標系角坐標系O-xyz.OA1(1，0，1）11(, 1)22FD(0，0，0）E1，1 ，），）12 例題例題.MCBA3)CB,cos2)BN1)AABANM2AA90BCA1CBCAABC,11111111o111 求證：求證：的值；的值