1、2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系1設計控制系統應完成哪些工作？設計控制系統應完成哪些工作？控制對象運動規律的描述控制對象運動規律的描述控制對象運動規律定性分析控制對象運動規律定性分析控制對象運動規律定量分析控制對象運動規律定量分析控制系統的設計與綜合控制系統的設計與綜合控制對象控制對象和和控制系統控制系統的的數學模型數學模型2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系2第二章 控制系統的數學模型2.1 2.1 控制系統的運動方程控制系統的運動方程2.2 2.2 線性系統的頻域模型線性系統的頻域模型2.3 2.3

2、 方框圖與信號流圖方框圖與信號流圖2.4 2.4 狀態空間與狀態空間表達式狀態空間與狀態空間表達式2.5 2.5 控制系統不同模型間的關系控制系統不同模型間的關系小小 結結2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系3本章學習要點簡單物理系統的微分方程的列寫；簡單物理系統的微分方程的列寫；非線性模型的線性化方法；非線性模型的線性化方法；傳遞函數和傳遞函數矩陣的概念；傳遞函數和傳遞函數矩陣的概念；結構圖和信號流圖的變換與化簡；結構圖和信號流圖的變換與化簡； 狀態空間與狀態空間表達式；狀態空間與狀態空間表達式；控制系統不同模型形式及其之間的轉換。控制系統不同模型

3、形式及其之間的轉換。2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系42.1 控制系統的運動方程dttduCtitutRidttdiLtuccr)()()()()()( 例例2.1.12.1.1研究研究RLCRLC電路，試找出輸出電壓電路，試找出輸出電壓u uc c(t)(t)隨輸入隨輸入電壓電壓u ur r(t)(t)變化的規律。變化的規律。解解R R、C C、L L以及初以及初始始u uc c(0)(0)確定時確定時, ,已已知知u ur r(t)(t)就可以確就可以確定定u uc c(t)(t)()()()(22tutudttduRCdttudLCrccc

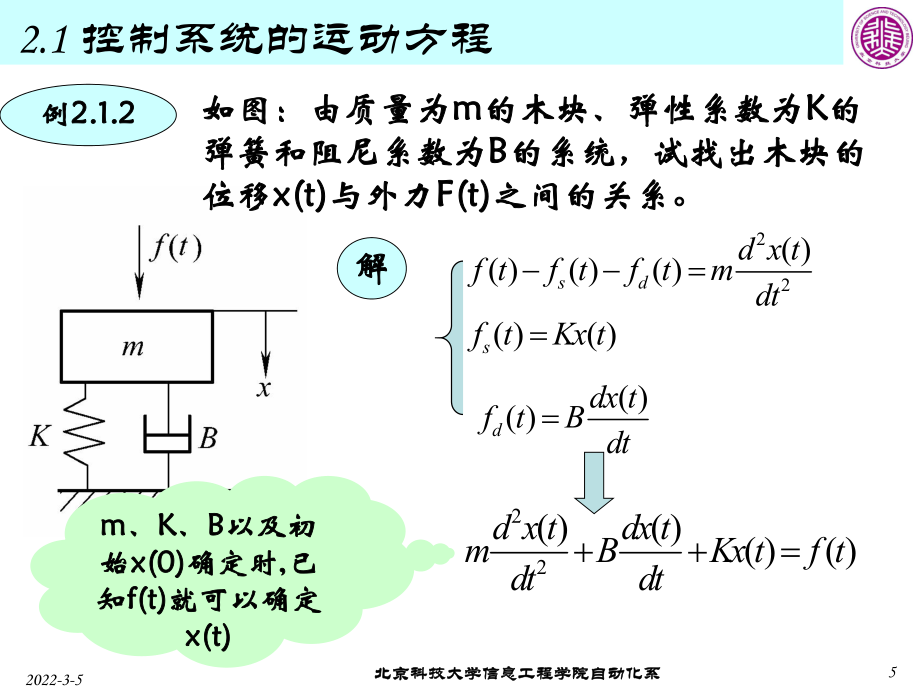
4、 2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系52.1 控制系統的運動方程例例2.1.22.1.2如圖：由質量為如圖：由質量為mm的木塊、彈性系數為的木塊、彈性系數為K K的的彈簧和阻尼系數為彈簧和阻尼系數為B B的系統，試找出木塊的的系統，試找出木塊的位移位移x(t)x(t)與外力與外力F(t)F(t)之間的關系。之間的關系。( ) ( )ddx tf tBdt22( )( )( )( )d x tdx tmBKx tf tdtdt22( )( )( )( ) sdd x tf tf tf tmdt( )( )sf tKx t解解mm、K K、B B以及初

5、以及初始始x(0)x(0)確定時確定時, ,已已知知f(t)f(t)就可以確定就可以確定x(t)x(t)2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系62.1 控制系統的運動方程 直流他勵電動機直流他勵電動機電樞電路，取電樞電壓電樞電路，取電樞電壓u ua a為輸入量為輸入量, ,電動機角電動機角速度速度m m為輸出量為輸出量, ,討論討論它們之間的關系。它們之間的關系。aaaaaaEtiRdttdiLtu )()()(電樞回路電壓平衡方程：電樞回路電壓平衡方程：電磁轉矩方程：電磁轉矩方程：ammtiCM)( 電動機軸上的轉矩平衡方程：電動機軸上的轉矩平衡方程

6、：)()()()()()()()(22tMRdttdMLtuCtCCfRdttdJRfLdttdJLcacaammemmammamamma )()()()(tMtMtfdttdJcmmmmm 例例2.1.32.1.3解解電樞反電勢電樞反電勢)(tCEea 是電樞電流產生的電動是電樞電流產生的電動轉矩轉矩是電動機轉矩系數是電動機轉矩系數mMmC是折合到電動機軸上的總負載轉矩是折合到電動機軸上的總負載轉矩(t)McJm:Jm:電動機和負載折合到電動機軸上的轉動慣電動機和負載折合到電動機軸上的轉動慣量；量；fm:fm:電動機和負載折合到電動機軸上的黏電動機和負載折合到電動機軸上的黏性摩擦系數；性摩擦

7、系數；2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系72.1 控制系統的運動方程 注意觀察三個示例的微分方程注意觀察三個示例的微分方程 可以通過求解得到可以通過求解得到ur(t)uc(t)，f(t)x(t)之間內在運之間內在運動的關聯關系、分析系統的運動特性。動的關聯關系、分析系統的運動特性。 進而改造系統進而改造系統-選擇適當的選擇適當的R、L、C和和m、B、K得得到希望的運動規律。到希望的運動規律。 許多表面上看來似乎毫無共同之處的控制系統，其許多表面上看來似乎毫無共同之處的控制系統，其物理背景可能完全一樣，物理背景可能完全一樣， 可以用一個運動方程來可以

8、用一個運動方程來表示，我們可以不單獨地去研究具體系統而只分析表示，我們可以不單獨地去研究具體系統而只分析其數學表達式，即它們具有相同的其數學表達式，即它們具有相同的數學模型數學模型。這類。這類系統被稱為系統被稱為相似系統相似系統。2.1.32.1.22.1.1例例例)()()()()()()()()()()()()()()()(222222tMRdttdMLtuCtCCfRdttdJRfLdttdJLtftKxdttdxBdttxdmtutudttduRCdttudLCcacaammemmammamammarccc2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系

9、82.1 控制系統的運動方程控制控制系統系統的運動的運動對系統施加控制（即輸入控制信號），對系統施加控制（即輸入控制信號），從而得到系統輸出量（即受控量）隨時間的變化規律從而得到系統輸出量（即受控量）隨時間的變化規律（即輸出響應信號）。（即輸出響應信號）。控制系統的運動方程控制系統的運動方程根據描述系統特性的物理學定律，根據描述系統特性的物理學定律，如機械，電氣，熱力，液壓等方面的基本定律寫出。如機械，電氣，熱力，液壓等方面的基本定律寫出。展示系統在運動過程中各變量之間的相互關系，既定展示系統在運動過程中各變量之間的相互關系，既定性又定量地描述整個系統的運動過程。性又定量地描述整個系統的運動過

10、程。 數學模型數學模型描述系統內部物理量（或變量）之間的數學描述系統內部物理量（或變量）之間的數學表達式，表達式，是分析和設計自動控制系統的基礎。是分析和設計自動控制系統的基礎。靜態模型：靜態模型：在靜態條件下（即變量不隨時間變化），描述變在靜態條件下（即變量不隨時間變化），描述變量之間關系的代數方程量之間關系的代數方程(組組)。動態模型：動態模型：描述變量各階導數之間關系的微分方程描述變量各階導數之間關系的微分方程(組組)。2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系92.1 控制系統的運動方程建立數學模型的方法建立數學模型的方法解析法解析法 依據描述系統

11、運動規律的運動定律來得依據描述系統運動規律的運動定律來得到微分方程的方法。到微分方程的方法。實驗法實驗法 基于系統輸入輸出的實驗數據來建立數基于系統輸入輸出的實驗數據來建立數學模型的方法。學模型的方法。數學模型的形式數學模型的形式時域模型時域模型微分方程、差分方程和狀態方程；微分方程、差分方程和狀態方程；復頻域模型復頻域模型傳遞函數、結構圖、頻率特性。傳遞函數、結構圖、頻率特性。2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系102.1 控制系統的運動方程 問題：從嚴格意義上講，絕大多數系統的數學模型都問題：從嚴格意義上講，絕大多數系統的數學模型都不是線性模型（

12、即系統并非是線性系統）。事實上，不是線性模型（即系統并非是線性系統）。事實上，任何一個元件總是存在一定程度的非線性。即使假設任何一個元件總是存在一定程度的非線性。即使假設具有線性的特性，也是局限在一定的范圍內。具有線性的特性，也是局限在一定的范圍內。幾幾種種常常見見的的非非線線性性2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系112.1 控制系統的運動方程兩類非線性系統兩類非線性系統具有具有連續變化連續變化的非線性系統的非線性系統 動態：動態：y(n)=f(t;y,y(1),y(n-1),x,x(1),x(m) 靜態：靜態：y=f(x)本質本質非線性系統非線性

13、系統 2),(1),(2),;(1),;(21)()1(2)()1(1)(條條件件條條件件靜靜態態：條條件件條條件件動動態態：xtfxtfyxxyyytfxxyyytfynnnnn2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系122.1 控制系統的運動方程 非線性微分方程的求解很困難。非線性微分方程的求解很困難。在一定條件下在一定條件下，近，近似地轉化為線性微分方程，可以使系統的動態特似地轉化為線性微分方程，可以使系統的動態特性的分析大為簡化。實踐證明，這樣做能夠圓滿性的分析大為簡化。實踐證明，這樣做能夠圓滿地解決許多工程問題，有很大的實際意義。地解決許多工程

14、問題，有很大的實際意義。線性化的方法線性化的方法忽略忽略弱弱非線性環節非線性環節：如果元件的非線性因素較弱或者不：如果元件的非線性因素較弱或者不在系統線性工作范圍以內，則它們對系統的影響很小，在系統線性工作范圍以內，則它們對系統的影響很小，就可以忽略。就可以忽略。 臺勞級數展開法臺勞級數展開法(小偏差法，切線法，增量線性化法小偏差法，切線法，增量線性化法)：適用前提適用前提假設在控制系統的整個調節過程中，各個元假設在控制系統的整個調節過程中，各個元件的輸入和輸出量只是在平衡點附近作微小變化。件的輸入和輸出量只是在平衡點附近作微小變化。2022-3-5北京科技大學信息工程學院自動化系北京科技大學

15、信息工程學院自動化系132.1 控制系統的運動方程202200)(!21)()(00 xxdxydxxdxdyyxfyxx0yyy 0 xxx 0 xdxdyk 忽略二次以上的各項，上式可以寫成：忽略二次以上的各項，上式可以寫成：A(x0,y0)平衡點，函數在平平衡點，函數在平衡點處連續可微，則可將函衡點處連續可微，則可將函數在平衡點附近展開成臺勞數在平衡點附近展開成臺勞級數：級數：xky其中：其中：非線性元件的線性化數學模型非線性元件的線性化數學模型2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系142.1 控制系統的運動方程平均斜率法平均斜率法：如果一非線性

16、元件輸入輸出關系如下圖：如果一非線性元件輸入輸出關系如下圖所示，此時不能所示，此時不能臺勞級數展開法臺勞級數展開法，可用平均斜率法得，可用平均斜率法得線性化方程為線性化方程為 ：kxy 11xyk 0 xyx1y1-x1-y1其中：其中：2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系152.1 控制系統的運動方程注意：注意：這幾種方法只適用于一些非線性程度較低的系統，這幾種方法只適用于一些非線性程度較低的系統，對于某些嚴重的非線性（本質非線性對于某些嚴重的非線性（本質非線性)不能作線性化處不能作線性化處理，一般用理，一般用相平面法相平面法及及描述函數法描述函數

17、法進行分析。進行分析。(此部分此部分超出本課程的內容，可參考非線性控制的章節或教超出本課程的內容，可參考非線性控制的章節或教材。材。)2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系162.1 控制系統的運動方程例例2.1.42.1.4 水位自動控制系統水位自動控制系統輸入量為輸入量為Q1 ,輸出量為水位輸出量為水位H，求水箱的微分方程。，求水箱的微分方程。水箱的橫截面積為水箱的橫截面積為C，R表示流阻。表示流阻。2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系17RHQ 2根據托里拆利定理，出水量與水位高度平方根成正比，則有：根

18、據托里拆利定理，出水量與水位高度平方根成正比，則有：R 1其中其中 為比例系數。為比例系數。水箱的線性化微分方程水箱的線性化微分方程: :整理得水箱的標準線性化微分方程為整理得水箱的標準線性化微分方程為: :22002001()2HQQHHQRH RRHR 02其中：其中：顯然這個式子為非線性關系顯然這個式子為非線性關系, , 在工作點在工作點 附近進行臺勞級數附近進行臺勞級數展開。取一次項得：展開。取一次項得：2.1 控制系統的運動方程解解在在 時間中，水箱內流體變化量時間中，水箱內流體變化量 . .則：則：dtCdH12()CdHQQ dt010120()()HCd HHQQQdtR注意：

19、注意： 是常數；是常數； 。0H1020QQ1d HHCQdtR 2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系182.1 控制系統的運動方程說明說明 本質非線性系統一般不可線性化。本質非線性系統一般不可線性化。 多變量情況處理類似。多變量情況處理類似。 工作點不同，所得線性化方程的線性化系工作點不同，所得線性化方程的線性化系數不同，即線性化方程不同。數不同，即線性化方程不同。 非線性系統的線性化方程只在非線性系統的線性化方程只在工作點附近工作點附近才成立才成立 。2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系192.2 線性

20、系統的復數域模型2.2.1 2.2.1 拉普拉斯變換拉普拉斯變換2.2.2 2.2.2 傳遞函數傳遞函數2.2.3 2.2.3 傳遞函數矩陣傳遞函數矩陣2.2.4 2.2.4 典型元部件及典型環節的傳遞函典型元部件及典型環節的傳遞函數數問題：問題： 1）微分方程求解比較困難，不利于工程實現；）微分方程求解比較困難，不利于工程實現； 2）有時分析控制系統的性質時不必求解方程；）有時分析控制系統的性質時不必求解方程； 是否有更方便的形式描述系統？是否有更方便的形式描述系統？2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系202.2 線性系統的復頻域模型 拉氏變換法是

21、一種數學積分變換，其核心是把時拉氏變換法是一種數學積分變換，其核心是把時間函數間函數f(t)與復變函數與復變函數F(s)聯系起來，把時域問題通過聯系起來，把時域問題通過數學變換為復頻域問題，把時間域的高階微分方程變數學變換為復頻域問題，把時間域的高階微分方程變換為復頻域的代數方程以便求解。換為復頻域的代數方程以便求解。 )( ) s ( tfF 簡簡寫寫對應對應 時域函數時域函數f f( (t t)( )(原函數原函數) )復頻域函數復頻域函數F(s)(F(s)(象函數象函數) ) js s s為復頻率為復頻率2.2.1 2.2.1 拉普拉斯變換拉普拉斯變換2022-3-5北京科技大學信息工程

22、學院自動化系北京科技大學信息工程學院自動化系212.2 線性系統的復頻域模型 ) s (21)( )() s (0dseFjtfdtetfFstjcjcst 正變換正變換反變換反變換 )( )()( )( SFtftfSF1簡簡寫寫正變換正變換反變換反變換象函數象函數F F(s) (s) 用大寫字母表示用大寫字母表示, ,如如I I(s)(s)，U U(s)(s)。原函數原函數f f(t) (t) 用小寫字母表示，如用小寫字母表示，如 i i(t), (t), u u(t)(t)。1 12 2象函數象函數F F(s) (s) 存在的條件：存在的條件： dtetfst0)(為為收收斂斂因因子子t

23、es 拉氏變換的定義拉氏變換的定義t t 0 0 , f, f( (t t)=0)=02022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系222.2 線性系統的復頻域模型如果存在有限常數如果存在有限常數MM和和c c使函數使函數f f( (t t) )滿足：滿足：), 0 )( tMetfctdtMedtetftct 00)s (s)(CM s則則 總可以找到一個合適的總可以找到一個合適的s s值使上式積分為值使上式積分為有限值，即有限值，即f f( (t t) )的拉氏變換式的拉氏變換式F(s)F(s)總存在。總存在。2022-3-5北京科技大學信息工程學院自動化

24、系北京科技大學信息工程學院自動化系232.2 線性系統的復頻域模型典型函數的拉氏變換典型函數的拉氏變換 (1)(1)單位階躍函數的象函數單位階躍函數的象函數)()(ttfdtettsFst0)()()( s1 (2)(2)單位沖激函數的象函數單位沖激函數的象函數)()(ttf 1)()()(0dtettsFst (3)(3)指數函數的象函數指數函數的象函數ate)t (f asdteeesFstatat1)(0 2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系242.2 線性系統的復頻域模型(4)(4)正正弦弦函數的象函數函數的象函數ttfsin)(220sin

25、sin)(sdte ttsFst (5)(5)余弦函數的象函數余弦函數的象函數ttfcos)(2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系252.2 線性系統的復頻域模型拉普拉斯變換的基本性質拉普拉斯變換的基本性質線性性質線性性質)()()()(2211sFtfsFtf , 若(s)FA(s)FA2211 )t(f)t(f2211AA 則則時間比例性質（相似定理）時間比例性質（相似定理）則),()( 若sFtf：( )()tL fFS其中其中為實常數為實常數2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系262.2 線性系統的

26、復頻域模型微分性質微分性質時域導數性質時域導數性質)(ss 0)()(fFdttdf則)()( sFtf若：頻域導數性質頻域導數性質)()(s Ftf設：ss ddFttf)()(則：)0()0()0()()()1()1(21nnnnnnffsfssFsdttfd)()(sFsdttfdnnn則：則：如果：如果：0)0()0()0()1()1( nfff2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系27積分性質積分性質)()(sFtf 設設：)(1)(0sFsdttf t 則：則：延遲性質延遲性質)()(sFtf 設設：)()(00sFettf st 則則：)

27、()(tfeLSFt 頻域延遲頻域延遲時域延遲時域延遲在時間域的平移變換在復數域有對應的衰減變換。在時間域的平移變換在復數域有對應的衰減變換。時間信號時間信號f(t)f(t)在時間域的指數衰減，其拉氏變換在在時間域的指數衰減，其拉氏變換在復數域有對應的坐標平移。復數域有對應的坐標平移。2.2 線性系統的復頻域模型2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系28)(lim)(lim)0(0SSFtffst )(lim)(lim)(0SSFtffst 初值定理初值定理f f( (t t) )和和 的拉氏變換存在，的拉氏變換存在， 也存在，也存在，則則dttdf)

28、( )limsSF S終值定理終值定理存在時存在時)(limtft f f( (t t) )和和 的拉氏變換存在，的拉氏變換存在， ，并且除在原點處唯一的極點外，并且除在原點處唯一的極點外，SF(S)SF(S)在包含在包含jj軸軸的右半平面是解析的（即的右半平面是解析的（即tt時，時，f(t)f(t)為常數），為常數），則則dttdf)(時域函數的初值，可以由變換域求得。時域函數的初值，可以由變換域求得。時域函數的終值，也可以由變換域求得。時域函數的終值，也可以由變換域求得。2.2 線性系統的復頻域模型2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系292.2

29、線性系統的復頻域模型例例2.2.12.2.1)()()()()(0)(0)1(1)(tubtubtyatyatymmnnn 已知微分方程如下，試求已知微分方程如下，試求初值皆為零時初值皆為零時輸輸出量的拉氏變換與輸入的拉氏變換之比。出量的拉氏變換與輸入的拉氏變換之比。解解)()()()()(0011sUbsUsbsYasYsasYsmmnnn 01101)()(asasbsbsbsUsYnnnmmmm 0)0()0()0()1()1( nyyy初值皆為零有初值皆為零有由微分性質對微分方程作拉氏變換得：由微分性質對微分方程作拉氏變換得：2022-3-5北京科技大學信息工程學院自動化系北京科技大學

30、信息工程學院自動化系302.2 線性系統的復頻域模型拉普拉斯反變換的求法拉普拉斯反變換的求法(1)(1)按定義按定義dsesFjtfstjcjc)(21)( (2)(2)對簡單形式的對簡單形式的F(s)F(s)可以查拉氏變換表得原函數可以查拉氏變換表得原函數(P28)(P28)f(t)f(t)F(s)F(s)f(t)f(t)F(s)F(s)(t)(t)1 1SintSint1(t)1(t)1/s1/sCostCostt t1/(s+a)1/(s+a)21 sate)(22s)(22ssteatsinteatcos22)( as22)(asas2022-3-5北京科技大學信息工程學院自動化系北京

31、科技大學信息工程學院自動化系31)()()()(2sFsFsFsFn1 )()()()(21tftftftfn (4)(4)把把F(S)F(S)分解為簡單項的組合分解為簡單項的組合部分分式部分分式展開法展開法(3)(3)利用拉氏變換的性質利用拉氏變換的性質的原函數。的原函數。求求其原函數為其原函數為已知：已知：)(sin)(,)(22asFttfssF 解解由延遲性質知：由延遲性質知：tetfeasFatat sin)()(1 思考思考的原函數的原函數22)()s ( asasF2.2 線性系統的復頻域模型例例2.2.22.2.22022-3-5北京科技大學信息工程學院自動化系北京科技大學信息

32、工程學院自動化系32為為真真分分式式，設設)(sFmn 利用部分分式可將利用部分分式可將F F(s)(s)分解為：分解為：象函數的一般形式：象函數的一般形式：)( ssss) s (U) s (Y) s (011011mnaabbbFnnnmmmm nnpskpskpsksF 2211)(tpntptpnekekektf 2121)(待定常數待定常數nUppn0) s (1 個個單單根根分分別別為為有有若若1)( ps)( ps)( ps)( ps2.2 線性系統的復頻域模型2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系332.2 線性系統的復頻域模型、n、i

33、 pssFkipsii321)( 待定常數的確定：待定常數的確定：方法方法1 1方法方法2 2) s (U)ps)(s (Ylimpisiik ) s (U) s (Y)ps)(s (Ylimp isi)p(U)p(Yii 求極限的方法求極限的方法2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系342.2 線性系統的復頻域模型6554)(2 ssssF例例2.2.32.2.3求如下象函數的原函數。求如下象函數的原函數。解解3s2s21 KK33s5s421 SK72s5s43s2 K解法解法1 16s5s5s4) s (2 F)(7)(3)(32tetetftt

34、 35s25s4)p(D)p(NK2s111 75s25s4(pD)p(NK3s222 )解法解法2 2原函數的一般形式：原函數的一般形式：tpnntptpnepDpNepDpNepDpNtf)()()()()()()(221121 2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系352.2 線性系統的復頻域模型一對共軛復根為一分解單元一對共軛復根為一分解單元,設：設： jj21pp)()(2) s (D)s)(s () s (N) s (D) s (N) s (112221sDsNssBsAjjF ) s (D) s (N)(s)(K)(sK11222221

35、sBKKAK 221, 222112212221121arccosarccos)()sin()(cossin)(KKKtftKKetfteKteKtfttt 其中：有有共共軛軛復復根根若若0) s (U 22022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系362.2 線性系統的復頻域模型例例2.2.42.2.4解解)(52)(2tfssssF的的原原函函數數求求 jp,的的根根： ss22222)1(12)1(1 ssstetetftt2sin212cos)( ).cos(. tet2222)1(1152)( ssssssF)0()4 .632sin(118. 1

36、 ttet2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系372.2 線性系統的復頻域模型nnnnnmmmmbbbF)ps (K)ps (K)ps (KpsK )ps (ss) s (11111121121111011 11)(limK11psnpsnsF)p(s 11)()(limK111psnpsnsFpsdsd 11)()!1(1limK11111psnnnpssF)p(sdsdn 其中：其中：具具有有重重根根若若0) s (U 32022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系382.2 線性系統的復頻域模型例例2.2.5

37、2.2.5解解)()()(tfssssF的的原原函函數數求求： )()(sKsKsK sssK)( sssK ssFsdsdK)()( sssdsd)0(344)( tteetftt )()(ssssF2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系392.2 線性系統的復頻域模型 n n = =m m 時將時將F F(s)(s)化成真分式和多項式之和化成真分式和多項式之和nnpsKpsKpsKAsF )(小結小結: :由由F F(s)(s)求求f( f(t) t)的步驟的步驟 求真分式分母的根，確定分解單元求真分式分母的根，確定分解單元 將真分式展開成部分分式

38、，求各部分分式的系數將真分式展開成部分分式，求各部分分式的系數 對每個部分分式和多項式逐項求拉氏反變換對每個部分分式和多項式逐項求拉氏反變換)()()(0sDsNAsF 2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系402.2 線性系統的復頻域模型例例2.2.62.2.6解解的的原原函函數數求求： sssssF)( sss ss)0()37()()(23 teettftt sssssF)(2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系412.2 線性系統的復頻域模型2.2.2 2.2.2 系統的傳遞函數系統的傳遞函數（1 1）

39、定義：）定義： 單輸入單輸出單輸入單輸出線性定常線性定常動態對象的傳動態對象的傳遞函數遞函數G(S)G(S)是是零初值零初值下該對象的輸出量的拉普拉斯下該對象的輸出量的拉普拉斯變換變換Y(S)Y(S)數與輸入量的拉普拉斯變換數與輸入量的拉普拉斯變換R(S)R(S)之比。之比。 回答本節開始的問題回答本節開始的問題( )( ) ( )Y SG SR S2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系422.2 線性系統的復頻域模型RLCRLC電路電路rcuuiRdtdiLcduiCdt取取u ur r為輸入，為輸入，u uc c為輸出，得為輸出，得: :22ccc

40、rd uduLCRCuudtdt拉氏變換得：拉氏變換得： 21crLCsRCsUsUs則傳遞函數為：則傳遞函數為：例例2.2.72.2.7解解2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系432.2 線性系統的復頻域模型例例2.2.82.2.8解解根據牛頓第二定律，得根據牛頓第二定律，得 22sdd x tf tftftmdt sftKx t ddx tftBdt取外力取外力f(t)f(t)為輸入；位移為輸入；位移x(t)x(t)為輸出為輸出 2msBsK X sF s 22d x tdx tmBKx tf tdtdt得微分方程：得微分方程：拉氏變換后得：拉氏

41、變換后得：傳遞函數為：傳遞函數為：2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系442.2 線性系統的復頻域模型 一般有一般有nm nm 。同一個系統，當輸入量和輸出量的選擇不相同時，可同一個系統，當輸入量和輸出量的選擇不相同時，可能會有不同的傳遞函數。能會有不同的傳遞函數。不同的物理系統可以有相同的傳遞函數不同的物理系統可以有相同的傳遞函數。傳遞函數表示系統傳遞輸入信號的能力，反映系統本傳遞函數表示系統傳遞輸入信號的能力，反映系統本身的動態性能。它只與系統的結構和參數有關，與外身的動態性能。它只與系統的結構和參數有關，與外部作用等條件無關。部作用等條件無關。

42、（2 2）傳遞函數的性質）傳遞函數的性質 G(s)G(s)與系統的微分方程有直接聯系。與系統的微分方程有直接聯系。G(s)G(s)是系統單位脈沖響應的拉氏變換是系統單位脈沖響應的拉氏變換y(t)G(s)(t)u(t)L2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系452.2 線性系統的復頻域模型（3）傳遞函數的常用表示形式）傳遞函數的常用表示形式 時間常數形式時間常數形式根的形式根的形式01110111.)()()(asasasabsbsbsbsDsNsGnnnnmmmm 2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系462.

43、2 線性系統的復頻域模型 212112211221)12()1()12()1()(nllllnkkmjjjjmiisqsqspssssTKsG 212112211221)2()()2()()(nllllnkkmjjjjmiigsspsswswsasKsG 時間常數；時間常數；，其中其中lkjiqpT .;22121nnnmmm 2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系472.2 線性系統的復頻域模型（4）傳遞函數局限）傳遞函數局限 G(s) G(s)原則上不反映原則上不反映y(0)0y(0)0時的系統的全部運時的系統的全部運動規律動規律. . G(s)G

44、(s)只適用于單輸入，單輸出系統。只適用于單輸入，單輸出系統。 G(s) G(s)只適用于線性定常系統只適用于線性定常系統由于拉氏變由于拉氏變換是一種線性變換換是一種線性變換. .2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系482.2 線性系統的復頻域模型特征多項式特征多項式：G(s)G(s)的分母多項式的分母多項式D(s)D(s)特征方程特征方程：D(s)=0D(s)=0極點極點/ /特征根特征根：D(s)=0D(s)=0的根的根零點零點：N(s)=0N(s)=0的根的根零極點對消零極點對消系統的階數系統的階數：max(n,m)max(n,m)，（一般，（

45、一般nmnm）系統的類型系統的類型放大系數放大系數與上述傳遞函數有關的幾個重要概念：與上述傳遞函數有關的幾個重要概念：系統的放大系數系統的放大系數 K K根軌跡放大系數根軌跡放大系數 KgKg零極點圖零極點圖2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系49G(s) G(s) 的零點、極點表示在的零點、極點表示在S S平面上平面上零極點圖零極點圖)22)(3()2()(2ssssKsGgG(s)G(s)G(s)G(s)零極點分布圖零極點分布圖 系統性能系統性能 G(s)G(s)2.2 線性系統的復頻域模型2022-3-5北京科技大學信息工程學院自動化系北京科技

46、大學信息工程學院自動化系502.2 線性系統的復頻域模型2.2.3 2.2.3 傳遞函數矩陣傳遞函數矩陣將傳遞函數的概念推廣到多輸入多輸出系統，傳遞將傳遞函數的概念推廣到多輸入多輸出系統，傳遞函數函數G（s）推廣為傳遞函數矩陣）推廣為傳遞函數矩陣G（s）。設系統。設系統有有p個輸入量、個輸入量、q個輸出量如下圖。個輸出量如下圖。G(s)u1u2up。y1y2yq。G(s)U(s)Y(s) )()()()()()()()()(G(s)212222111211sgsgsgsgsgsgsgsgsgqpqqpp2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系512.2

47、線性系統的復頻域模型例例2.2.92.2.9如圖，直流他勵電動機；如圖，直流他勵電動機；u ua a是外加的輸入是外加的輸入變量電樞電壓（伏），變量電樞電壓（伏），mm表示電動機的角表示電動機的角轉速（弧度轉速（弧度/ /秒），為輸出量。討論它們之秒），為輸出量。討論它們之間的關系。間的關系。2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系522.2 線性系統的復頻域模型由例由例2.1.32.1.3系統運動方程為：系統運動方程為：)()()()()()()()(22tMRdttdMLtuCtCCfRdttdJRfLdttdJLcacaammemmammamamm

48、a 解解)()()()()()()()(2sMRssMLsUCsCCfRssJRfLssJLcacaammemmammamamma )()()()(1)(2sMsURsLCCCfRsJRfLsJLscaaaeemmamamamam 拉氏變換得：拉氏變換得：整理得：整理得：2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系53 比例環節比例環節21crrRxxKxR )()(sKXsXrcKsXsXsWrc)()()( 控制系統通常由若干個控制系統通常由若干個基本部件基本部件組合而成，這些基本部件組合而成，這些基本部件稱為典型環節。稱為典型環節。 包括：包括：比例環

49、節比例環節、微分環節微分環節、積分環節積分環節、比例微分環節比例微分環節、一階慣性環節一階慣性環節、二階振蕩環節二階振蕩環節和和延遲環節延遲環節。（1 1） 典型環節典型環節2.2 線性系統的復頻域模型2.2.4 2.2.4 典型元部件及典型環節的傳遞函數典型元部件及典型環節的傳遞函數2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系54比例環節的比例環節的單位階躍響應單位階躍響應KsXsXsWrc)()()(ssXr1)(當 時2.2 線性系統的復頻域模型2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系55 一階慣性環節一階慣性環

50、節( )1( )( )1crXsW sXsTsssXr1)(當 時，01/( )( )( )(1)(1/)1/crAAKK TXsW s Xss Tss sTssT00(1)sK TAsKs sTKTsTssTKATs/11)/1()/1(/11( )(1/ )cX sKssT微分方程是一階的微分方程是一階的, ,且輸出響應需一定且輸出響應需一定的時間才能達到穩態值。的時間才能達到穩態值。其中其中T T為慣性環節的時間常數。為慣性環節的時間常數。2.2 線性系統的復頻域模型2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系56慣性環節的慣性環節的單位階躍響應單位階

51、躍響應11( )(1/)cXsKssT/( )(1),0t Tcx tKet求拉氏反變換得求拉氏反變換得 2.2 線性系統的復頻域模型2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系57 積分環節積分環節( )1( )( )crUsKW sUssTs其中其中K=K=1 1/T /T ， T T為積分環節的時間常數，表示積分的快慢程度。為積分環節的時間常數，表示積分的快慢程度。積分環節的積分環節的單位階躍響應單位階躍響應2.2 線性系統的復頻域模型2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系58 微分環節微分環節sKsUsUsW

52、rc)()()(其中其中K K為微分環節的為微分環節的時間常數，表示微分時間常數，表示微分速率的大小。速率的大小。2.2 線性系統的復頻域模型 理想微分環節理想微分環節 一階微分環節（又稱比例微分環節、一階微分環節（又稱比例微分環節、實用微分環節）實用微分環節） 2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系59 二階振蕩環節二階振蕩環節這種環節包括有這種環節包括有兩個儲能元件兩個儲能元件，當輸入量發生變化時，當輸入量發生變化時，兩種儲能元件的能量相互交換。在階躍函數作用下，其兩種儲能元件的能量相互交換。在階躍函數作用下，其暫態響應可能作周期性的變化。暫態響應

53、可能作周期性的變化。 222( )2nnnW sss式中：式中：n 自然振蕩角頻率自然振蕩角頻率 阻尼比阻尼比由二階微分方程描述的系統。由二階微分方程描述的系統。2.2 線性系統的復頻域模型2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系60當輸入量為階躍函數時，輸出量的拉氏變換為：當輸入量為階躍函數時，輸出量的拉氏變換為：當當 時，上式特征方程的根為共軛復數。時，上式特征方程的根為共軛復數。1因式分解得：因式分解得：222( )(2)ncnnXss ss2221( )2ncnnsXssss振蕩環節的振蕩環節的單位階躍響應單位階躍響應：輸出量為輸出量為 ：22(

54、 )1sin(1)1ntcnex tt 21arctan2.2 線性系統的復頻域模型2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系61 延遲延遲/ /時滯環節時滯環節2.2 線性系統的復頻域模型帶鋼厚度檢測環節帶鋼厚度檢測環節 ()cdh th t vl ()crxtx tsrcesXsXsW)()()(寫成一般形式寫成一般形式 : :零初始條件下，拉氏變換為零初始條件下，拉氏變換為 傳遞函數為傳遞函數為 例例)()(sXesXrsc 2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系62時滯環節的輸出量時滯環節的輸出量 ()cd

55、h th t 232311( )112!3!W sssss時滯環節的傳遞函數時滯環節的傳遞函數srcesXsXsW)()()( 對于對于時滯時間很小時滯時間很小的時滯環節，常把它展開成泰勒級數，的時滯環節，常把它展開成泰勒級數，并略去高次項，得：并略去高次項，得：時滯環節時滯環節在一定條在一定條件下可近件下可近似為慣性似為慣性環節！環節！2.2 線性系統的復頻域模型2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系632.2 線性系統的復頻域模型2.2.4 2.2.4 典型元部件及典型環節的傳遞函數典型元部件及典型環節的傳遞函數元部件名稱元部件名稱傳遞函數傳遞函數

56、電位器電位器測速電機測速電機電加熱爐電加熱爐單容水槽單容水槽雙容水槽雙容水槽KsG )(KssG )(1)( TsKsG1)( TsKsGseTsKsG 1)(1)()(21221 sTTsTTKsG（2 2） 典型元部件典型元部件(有純延遲有純延遲)(也可有延遲，略也可有延遲，略)2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系642.3 方框圖與信號流圖控制系統的結構圖是由許多對信號進行單向運算的控制系統的結構圖是由許多對信號進行單向運算的方框和一些信號流向線組成，它包含方框和一些信號流向線組成，它包含4種基本單元。種基本單元。2.3.1 2.3.1 系統動

57、態結構圖系統動態結構圖 1）信號線）信號線 2）引出點（或測量點）引出點（或測量點）3）比較點（或綜合點）比較點（或綜合點）4）方框（或環節）方框（或環節）2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系652.3 方框圖與信號流圖+_ _+_ _+_ _Ka11C s21C s21R1R( )R s( )C s1( )U s1( )Us1( )U s1( )I s1( )I s2( )Is2( )Is2( )Is( )C s(b)1( )i t2( )it1( )u t( )c t( )r t1R2R1C2C(t)iR(t)ur(t)111(t)dti(t)i

58、C1(t)u2111(t)iRc(t)(t)u221(t)dtiC1c(t)222022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系662.3 方框圖與信號流圖+_ _+_ _+-11C s21R21C s11R( )R s( )C s1( )i t2( )it1( )u t( )c t( )r t1R2R1C2C思考思考:將兩部分電路分開分將兩部分電路分開分別討論然后在結合到一起別討論然后在結合到一起結果和前面得到的是否相結果和前面得到的是否相同同?2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系672.3 方框圖與信號流圖速度控制

59、系統速度控制系統例例2.3.12.3.12022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系682.3 方框圖與信號流圖解解（1）比較環節和速度調節器環節）比較環節和速度調節器環節 0rrUsIsR 1111111kkcUsUssIss RRC s式中：式中：00014TR C111RC式中：式中：rufu2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系692.3 方框圖與信號流圖式中式中10cRKR 110111kCrfsUsKUUssT s整理得整理得 2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化

60、系702.3 方框圖與信號流圖（2）速度反饋的傳遞函數）速度反饋的傳遞函數 fsfUsK n s式中：式中： 為速度反饋系數為速度反饋系數 sfK2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系712.3 方框圖與信號流圖（3）電動機及功率放大裝置）電動機及功率放大裝置 dskUsK Us 1dedddUsC n sIsRT s edzmdCIsIsTsn sRdtdnJCiCidtdiLiRnCummzmdddddedemdmmdddCCRJTRLT,2022-3-5北京科技大學信息工程學院自動化系北京科技大學信息工程學院自動化系722.3 方框圖與信號流圖（