1、奮斗沒有終點任何時候都是一個起點第(3)題(4)已知等差數(shù)列an的公差d 0,且a1，a3,a13成等比數(shù)列，若a1 1,Sn是數(shù)列an的前n項的2s 16和，則 n (nan 3* . . . .N )的最小值為()天津一中2015-2016-2高三數(shù)學(xué)(理)第二次考前沖刺熱身試卷本試卷共三道大題，共 150分，考試用時120分鐘.一、選擇題：本題共 8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項符合題目的要求.(1)若集合 A y y 2x , B x x2 2x 3 0, x R ,那么 AI(Cu B)().(A) Q3(B)1,3(C) 3,(D) 0, 13,y

2、x(2)已知實數(shù)x, y滿足 x y 1,則目標(biāo)函數(shù)z 2x y 1的最大值為().y 1，一1，一(A)3(B)(C)4(D)52(3)閱讀下邊的程序框圖，運行相應(yīng)的程序，若輸入 x的值為1,則輸出S的值為().(A) 4(B)(C) 2. 3-2(D)(5)已知 p:|x 1 |(A) 0 a 12(6)已知雙曲線與 a物線準(zhǔn)線的距離為(A).(A)0,a2, q:|x|p是q的必要不充分條件，則實數(shù)a的取值范圍是()(B)(C) a 1(D)24 1(a,b 0)與拋物線y2 4x共焦點, b雙曲線與拋物線的一公共點到拋2,雙曲線的離心率為e,則2e b2的值是(B) 2 21,且x(B

3、) y(C) 4 2 . 2log 1 1 ab,E)(C) x y(D) 4logba ,則x, y, z的大小關(guān)系是(D) z(A) 64(B) 73(C) 512(D) 585a =2i(8)(0,信達設(shè)函數(shù)f(x)在R上存在導(dǎo)數(shù))上 f (x) x,若 f(2 a)有 f ( x)f(x)x2,且在f (a) 2 2a ,則實數(shù)a的取值范圍為(奮斗沒有終點任何時候都是一個起點信達(A)(,0(B) (0,1)(C)(- ,1(D) 1,)二、填空題：本大題共6小題，每小題5分，共30分.把答案填在題中橫線上.(9)在復(fù)平面內(nèi)，復(fù)數(shù)- (1 2i)2的共軻復(fù)數(shù)對應(yīng)的點位于第1 i(10)

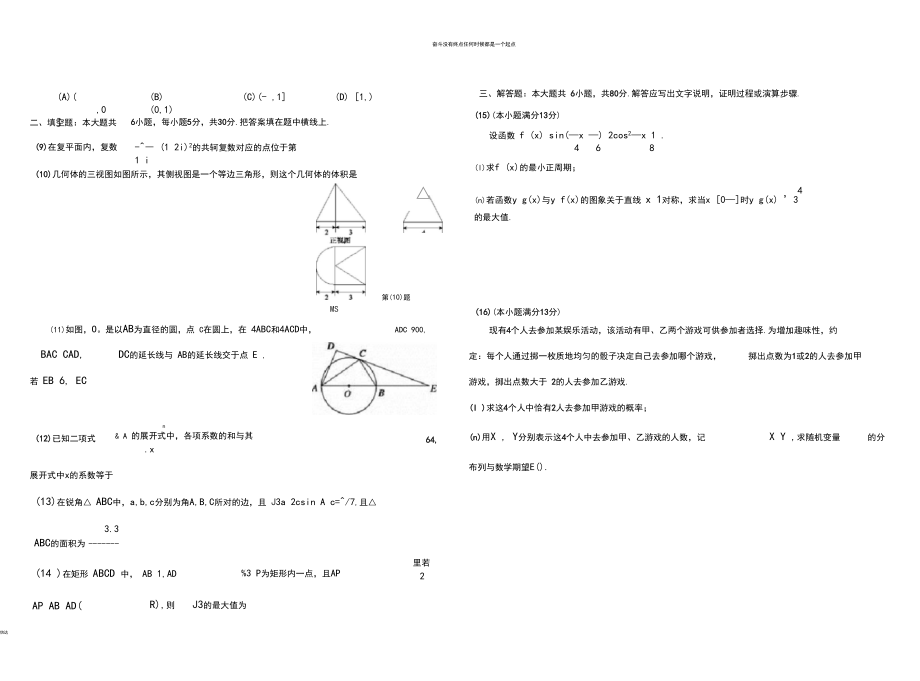
4、幾何體的三視圖如圖所示，其側(cè)視圖是一個等邊三角形，則這個幾何體的體積是第(10)題MS(11)如圖，O。是以AB為直徑的圓，點 C在圓上，在 4ABC和4ACD中，ADC 900,BAC CAD,DC的延長線與 AB的延長線交于點 E ,若 EB 6, EC(12)已知二項式n& A 的展開式中，各項系數(shù)的和與其.x展開式中x的系數(shù)等于64,(13)在銳角 ABC中，a,b,c分別為角A,B,C所對的邊，且 J3a 2csin A c=/7,且3.3ABC的面積為(14 )在矩形 ABCD 中， AB 1,AD%3 P為矩形內(nèi)一點，且AP里若2AP AB AD(R),則J3的最大值為三

5、、解答題：本大題共 6小題，共80分.解答應(yīng)寫出文字說明，證明過程或演算步驟.(15)(本小題滿分13分)設(shè)函數(shù) f (x) sin(x ) 2cos2x 1 .468(l)求f (x)的最小正周期；4(n)若函數(shù)y g(x)與y f(x)的圖象關(guān)于直線 x 1對稱，求當(dāng)x 0時y g(x) 3的最大值.(16)(本小題滿分13分)現(xiàn)有4個人去參加某娛樂活動，該活動有甲、乙兩個游戲可供參加者選擇.為增加趣味性，約定：每個人通過擲一枚質(zhì)地均勻的骰子決定自己去參加哪個游戲，擲出點數(shù)為1或2的人去參加甲游戲，擲出點數(shù)大于 2的人去參加乙游戲.(I )求這4個人中恰有2人去參加甲游戲的概率；(n)用X

6、 , Y分別表示這4個人中去參加甲、乙游戲的人數(shù)，記X Y ,求隨機變量的分布列與數(shù)學(xué)期望E().(17)(本小題滿分13分)如圖，已知正方形 ABCD和矩形ACEF所在的平面互相垂直，AB J2 , AF 1,M是線段EF的中點.(I)求證：AM 平面BDE ；(n)求二面角 A DF B的大小；(出)試在線段 AC上確定一點P,使得PF與CD所成的角是60o.(18)(本小題滿分13分)n 11已知數(shù)列an的前n項和Snan 彳 2(n N*),數(shù)列bn滿足bn 2n an.(i)求證：數(shù)列 bn是等差數(shù)列，并求數(shù)列 an的通項公式；(n)設(shè) cnlog 2-an225,數(shù)列 的刖n項和為

7、Tn,求滿足Tn (n N*)的n的最大值.CnCn 221(19)(本小題滿分14分)22x y橢圓C：= 匕 1(a b 0)的中心在原點，焦點在 x軸上，焦距為2,且與橢圓 a b2x2 1有相同離心率.2(I)求橢圓C的方程；(n)若直線l:y kx m與橢圓C交于不同的 A, B兩點，且橢圓C上存在點Q ,滿足OA OB OQ, (O為坐標(biāo)原點)，求實數(shù) 取值范圍.(20)(本小題滿分14分)已知函數(shù)f (x) ln(x a).x(i)若a 1,證明：函數(shù)f x是0, 上的減函數(shù)；(n)若曲線y f x在點1,f 1 處的切線與直線 x y 0平行，求a的值；ln x 1 x(出)若

8、x 0,證明： (其中e 2.71828 是自然對數(shù)的底數(shù)).x e 1A.提示：由a2a1a13得到(a1 2d)2a1(a112d), d 2(d(5)C.(6)D.B.得到Sn所求的式子提示：p: xp: 32n n(n 1) n .2n2 161 (nx 1,提示：由拋物線的焦點1) 2 33,q ： x(n1)F(1,0),得到 a2設(shè)公共點 P0(x0,y0), x0 1 2, x0從而口a提示：提示:0 x 1, y數(shù)學(xué)(理)第二次沖刺熱身參考答案(8)C.提示：令g、選擇題：本大題共 8小題，每小題5分，滿分(1)A.提示:0 ,B xx(2)C.提示:1包一上相父于點1(3)

9、B.提示:1,S1;x 2,SA(2, 1),9;x 4,S3或x1-9-2n 1a,由已知得b2 1.3,1.1，代入到拋物線方程得到2V。4,4-，2F 1. 得至Ua2 3 b22 2,b22,2e b2log 1 ababx f (x)10,a b 1,-2a 1, 01,zlog 1 ab1 logbb0.x) f(x)2得到g(x) g( x) 0,g(x)為奇函數(shù).又 g (x)單調(diào)遞增，而由奇函數(shù)性質(zhì)得到(2 a)2 a22 2a , f (2二、填空題:本大題6小題，每小題(9)提示:5 9.-一 一 i,z2 2f (x)0,g(x)在(0,g(x)在R上單調(diào)遞增.已知f(

10、25分，滿分30分.5 9. i .2 2a)f(a)a a.4. 3. .(10) 8用 4+ 提示：幾何體是一個半圓錐與一個四棱錐的組合體，設(shè)圓錐的體積為3Vi,四A(0,0), B(1,0),C(1，V3),D(0，V3).棱錐的彳積為V2 ,高為h ,則設(shè) P(x,y),則uuuAPuuuUULT_(x,y), AB (1,0), AD (0,73).代入 AP AB AD(,R),h16-4V233又因為 0 y(11) 2/3 提示：連接OC ,得BAC OCA.1, 不234又 BACCAD CADOCA.有 OCA ACD CADACD90°.x y J荻下岑(當(dāng)且僅

11、當(dāng)x y號時取得最大值).OC DE ,DE OO的切線于2是 CE BE AE,AE 12, AB 6 .三、解答題：本大題 6小題，滿分80分.由 ECBCAB, EE ,得到 BCE與 ACE相似.(15)本題滿分13分.AC CE，AC 夜BC已知AB為。的直徑，則ACB是直角.在Rt:A ACB中，由勾股定理,解得 BC(12) 135.提示：令x 1 ,得4n264,即2n 64, n 6.Tr1 C”1,r2, T3135(13) 5 .提示：由正弦定理,.3sin A 2sin Csin A,Q sin A0 sinC =2在銳角 ABC中,C .QS3-absinC 2332

12、由余弦定理,2ab cosC ,即7 (ab)2 12(ab)225,a b(14).提示:2以A為原點AB所在直線為x軸,AD所在直線為y軸建立直角坐標(biāo)系則解：(I) f(x) = sin xcos cosxsin cos x 2分46464=-sin x - cos x = V3sin( x )4分242443 .一 ，一,2-故f(x)的最小正周期為T 86分4(n )在y g(x)的圖象上任取一點(x, g(x),它關(guān)于x 1的對稱點(2 x,g(x)-7分由題設(shè)條件，點(2 x,g(x)在yf(x)的圖象上，從而g(x) f(2 x),3sin- (2 x)43=V3 sin一 一x

13、 一 = V3 cos(x )10 分2 4343、“4 .2當(dāng) x 0, 1 時，一一 x ,1133433分43因此y g(x)在區(qū)間0,一上的最大值為g(x)max g(0) 3 cos .13 分332(16)本題滿分13分.解：(I )依題意，這4個人中，每個人去參加甲游戲的概率為1 ,去參加乙游戲的概率為2 .33設(shè)“這4個人中恰有i人去參加甲游戲”為事件Ai （i 0,1,2,3,4）,則點N,E的坐標(biāo)分別是這4個人中恰有2人去參加甲游戲的概率P(A2) C2(1)2(|)233827(n)的所有可能取值為0,2,4 .由于兒與A3互斥,Ao與A4互斥,P(0)P(A2)P(2)

14、P(A)P(A)4081 'P(4)P(A2)P(A4)178111分所以的分布列是024P()84017278181所以隨機變量的數(shù)學(xué)期望E( ) 08 c 40一 2278117148818113分（17）本題滿分13分.解：（I ）記AC與BD的交點為N ,連接NE ,四邊形ACEF是矩形，N,M分別是AC,EF的中點,四邊形 ANEM是平行四邊形， AM / NE . NE 平面 BDE , AM 平面 BDE ,BDE . 4分（n）建立如圖所示的空間直角坐標(biāo)系A(chǔ)M / 平面2分?,0) , (0,0,1 ),點A,M的坐標(biāo)分別是（J2,j20）,（咚，咚,1）,uurNE

15、=AF uur .ABuur 又 NEAB, AD AB, AD I AF A ,，AB 平面 DAF .（衣,0,0）為平面DAF的法向量.41r/ 、2 V 2db=(2",2",1)(我,泥,0)uuir uurNE NFNE為平面uuuir0,BDF法向量.uuuu又 cos NE, AB1 uur . uutr一，AB與NE的夾角是260o.即所求二面角A DF B的大小是60o. 9分(m)設(shè) P(t,t,0)uur則 PF ( 2 t, . 2 t,1),又 PF與CD所成的角是ocos60解得t 或t2（18）本題滿分解：（I）在Sn當(dāng)n 2時，Sn 110

16、uuirCD (J2,0,0).60o,(2 t) 2t)2 1211分13分.an g)n11 nan 1(3)，即點（C t）2P是AC的中點.2 中，令 n 1 ,可得 aSa1 1 2 , a12 o2,13分.1 n 11 n 11所以 an Sn Sn 1 an 3n 1 (一) .即 2a0 an1+(一) , 2nan 2n 1 an 1 1 .22而 bn2n an,所以 bnbn 11.設(shè) A(。yj(x2, y2),Q(xQ, yQ),于即當(dāng) n 2 時，bn bn 1 1 ,又 b1 2a1 1,4 km一 2 ，2k2所以，數(shù)列bn是首項和公差均為1的等差數(shù)列.2my

17、 y2 k(x1 X2) 2m 21 2k2是bn 1(n1) 1 n,所以40時，易知點A,B關(guān)于原點對稱，則(n)因為cnlog2 log 2 2nan所以cncn2 n (n2)此時,uuu由OATn(113)1 (214)1 (315)1 ( n1)1111(- ) 1 -n n 22 n 110分0時，易知點uuuOBA, B不關(guān)于原點對稱，則uuirOQ ,得1 /Xq 一 (Xi1 , yQ 一(y1x2 ),y2),yQ4 kmZ2- , (1 2k )2mZ 2" . (1 2k )11分竺，即211342Q點在橢圓上，%廠2 2一也一22.(1 2k2)(1 2k

18、2)化簡得4m2(1 2k2)2(1 2k2)2.1 2k2 0, 4m212分2(1 2k2).單調(diào)遞減,11丁1342，由兩式可得 24,22且 0 .n的最大值為4.13分綜上可得實數(shù)的取值范圍是22.14分(19)本題滿分14分.2c 2,解：(I)由已知可 c 拒解得a ，2, b 1. 3分-.c 1,a 2(20)本題滿分14分.解：(I)當(dāng)a 1時，函數(shù)f x的定義域是1,0 U 0,2所求橢圓C的方程人 y21 . 4分2In x 1(II )建立方程組y kx m,x2 2y2 2,消去y,整理得(1 2k2)x224kmx 2 m2 0._22_2_2_22 16k m 4(1 2k )(2m2) 8(1 2k m ) .由于直線直線l與橢圓C交于不同的A, B兩點，故g x是0,上的減函數(shù)，所以 g x g 0ln1 0.所以f x 0,函數(shù)f x是0, 上的減函數(shù).(n )由題意知，f x x 11,一 1a即ln 1 a 1,