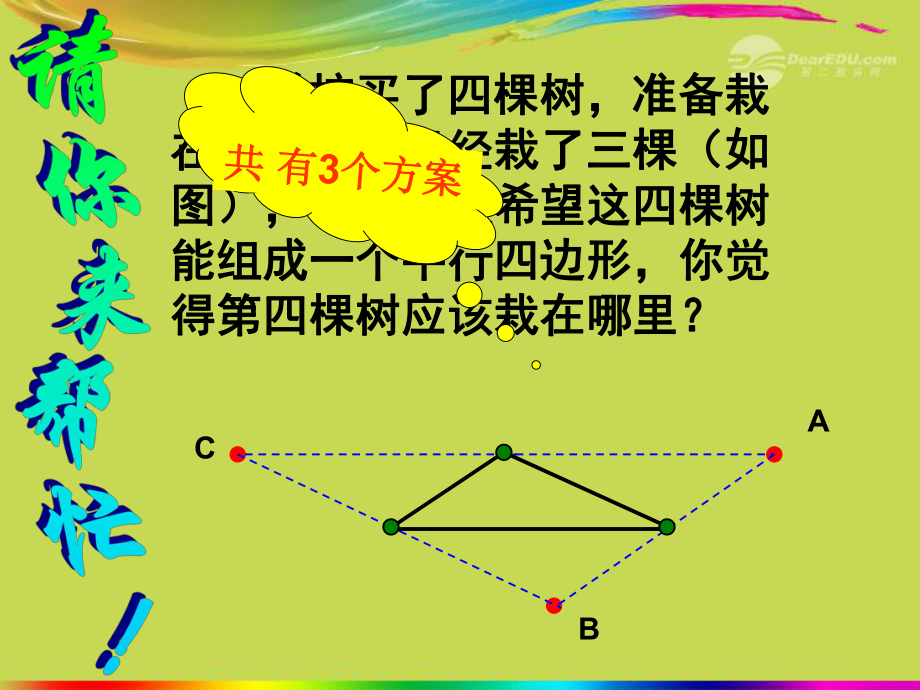
1、 學校買了四棵樹，準備栽在學校買了四棵樹，準備栽在花園里，已經栽了三棵（如圖），花園里，已經栽了三棵（如圖），現在學校希望這四棵樹能組成一現在學校希望這四棵樹能組成一個平行四邊形，你覺得第四棵樹個平行四邊形，你覺得第四棵樹應該栽在哪里？應該栽在哪里？學校買了四棵樹，準備栽學校買了四棵樹，準備栽在花園里，已經栽了三棵（如在花園里，已經栽了三棵（如圖），現在學校希望這四棵樹圖），現在學校希望這四棵樹能組成一個平行四邊形，你覺能組成一個平行四邊形，你覺得第四棵樹應該栽在哪里？得第四棵樹應該栽在哪里？學校買了四棵樹，準備栽學校買了四棵樹，準備栽在花園里，已經栽了三棵（如在花園里，已經栽了三棵（如圖），

2、現在學校希望這四棵樹圖），現在學校希望這四棵樹能組成一個平行四邊形，你覺能組成一個平行四邊形，你覺得第四棵樹應該栽在哪里？得第四棵樹應該栽在哪里？學校買了四棵樹，準備栽學校買了四棵樹，準備栽在花園里，已經栽了三棵（如在花園里，已經栽了三棵（如圖），現在學校希望這四棵樹圖），現在學校希望這四棵樹能組成一個平行四邊形，你覺能組成一個平行四邊形，你覺得第四棵樹應該栽在哪里？得第四棵樹應該栽在哪里？ABC共共 有有3個方案個方案平行四邊形平行四邊形的性質：的性質：邊邊平行四邊形的對邊平行平行四邊形的對邊平行平行四邊形的對邊相等平行四邊形的對邊相等角角平行四邊形的對角相等平行四邊形的對角相等對角線對角線

3、平行四邊形的對角線互平行四邊形的對角線互相平分相平分對稱性對稱性中心對稱圖形中心對稱圖形( (不是軸對稱圖形不是軸對稱圖形) )平行四邊形的鄰角互補。平行四邊形的鄰角互補。請同學們想想，你有多少種請同學們想想，你有多少種方法可以判別平行四邊形了？方法可以判別平行四邊形了？ DCAB從邊、對角線等方面說出判別平行從邊、對角線等方面說出判別平行四邊形方法四邊形方法 從邊看從邊看從對角線看從對角線看兩組對邊分別平行兩組對邊分別平行一組對邊平行且相一組對邊平行且相等等兩組對邊分別相等兩組對邊分別相等 對角線互相平分對角線互相平分 四邊形是平行四邊形四邊形是平行四邊形 例例 如圖，如圖， ABCDABC

4、D中，點中，點E E、F F分別在分別在ABAB、CDCD上且上且AE=CF AE=CF 。四邊形四邊形DEBFDEBF是平行四是平行四邊形嗎？邊形嗎？ 說說理由。說說理由。BCDAEF1 1、已知：、已知：E E、F F是平行四邊形是平行四邊形ABCDABCD對角線對角線ACAC上的兩點，并且上的兩點，并且BEDFBEDF試說明四邊形試說明四邊形BFDEBFDE是平行四邊形是平行四邊形CDABEF思路：只要說明思路：只要說明BE=DFBE=DF即可得到即可得到四邊形四邊形BFDEBFDE是平是平行四邊形行四邊形2 2、已知：、已知：E E、F F是平行四邊形是平行四邊形ABCDABCD對角線

5、對角線ACAC上的兩點，并且上的兩點，并且AE=CFAE=CF。四邊形四邊形BFDEBFDE是平行四邊形嗎？為什么？是平行四邊形嗎？為什么？DOABCEF思路：作對角線思路：作對角線BDBD，交，交ACAC于點于點O O。四邊形四邊形BFDEBFDE是平行四邊形是平行四邊形OF=OEOF=OE對角線互相平分對角線互相平分3.3.已知：如圖，已知：如圖，ABCDABCD的對角線的對角線ACAC，BDBD相交于點相交于點O,O,過點過點O O的直線與的直線與AD,BCAD,BC分別相交于點分別相交于點E,F.E,F.試說明試說明OE=OF.OE=OF.ABCDFEO例例 已知已知: ABCD: A

6、BCD中中, ,對角線對角線ACAC與與BDBD交于點交于點O,O,直線直線EFEF過點過點O O分別交分別交BCBC、ADAD于點于點E E、F F，G G、H H分別為分別為OBOB、ODOD的的中點。四邊形中點。四邊形 EGFHEGFH是平行四邊形是平行四邊形嗎？試說明理由嗎？試說明理由F FCAE EBDOH HG G 在在 ABCDABCD中，中，BADBAD、BCDBCD的平分線的平分線分別交分別交BCBC、ADAD于于E E、F F，四邊形，四邊形AECFAECF是是平行四邊形嗎？說明理由平行四邊形嗎？說明理由ADBCEF如圖，如圖，E E、F F分別是分別是ABCDABCD的一組對邊的一組對邊BC BC 、 ADAD上兩點，且上兩點，且AF=CEAF=CE，G G 、 H H分別是分別是AEAE與與CFCF的中點。四邊形的中點。四邊形GEHFGEHF是平行四邊形嗎？請說是平行四邊形嗎？請說明理由。明理由。FEDCABGH平行四邊形知識的運用平行四邊形知識的運用包括三個方面包括三個方面1 1、直接運用平行四邊形的、直接運用平行四邊形的性質性質解決解決某些問題；某些問題；2 2、判別判別四邊形是平行四邊形；四