第9章線性離散系統的分析與校正9.1離散系統的基本概念

9.2信號的采樣與保持9.3

Z變換理論9.4※※線性離散控制系統的數學模型（描述）9.5※線性離散控制系統分析9.6※※線性離散控制系統的數字校正（設計）主要內容離散系統分析的數學基礎9.３

Z變換理論※※線性連續系統線性離散系統1穩——穩定性2快——

動態性能3

準——

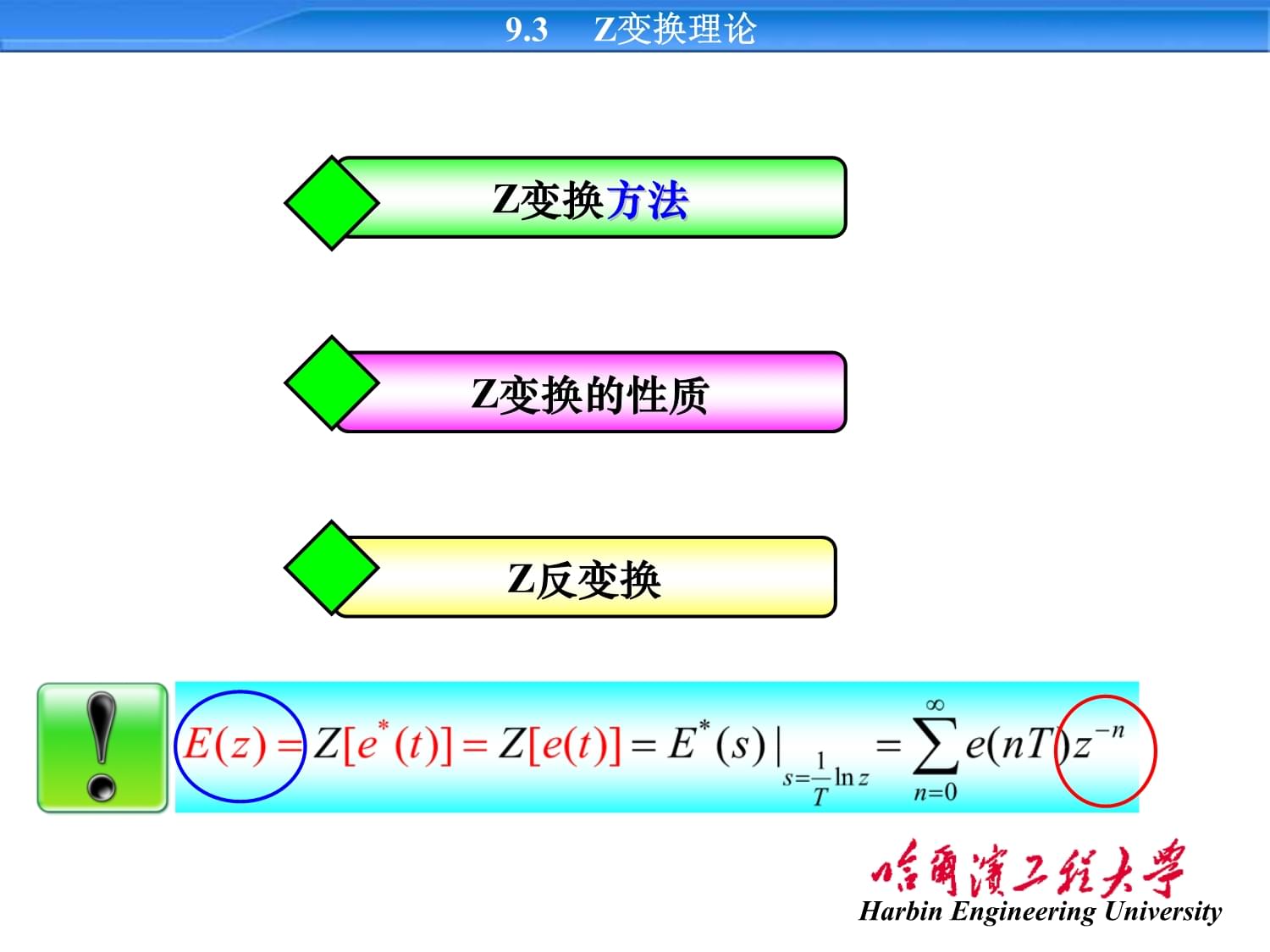
穩態性能拉氏變換Z變換相當于離散系統的拉氏變換一、Z變換定義(P43)9.3

Z變換理論設連續函數e(t)是可拉氏變換的,則局限：只反映采樣點上信息則采樣信號的Z變換定義為

Z變換的性質Z變換方法Z反變換9.3

Z變換理論Z變換方法1.※

級數求和法2.※部分分式法3.

留數法（補充）主要思想（P43）：根據Z變換定義式寫出級數形式的Z變換：再作級數求和，得到閉合形式的Z變換表達式。9.3

Z變換理論二、※Z變換方法(P43)例2.5：試求單位階躍函數e(t)=1(t)的Z變換。9.3

Z變換理論---1.級數求和法二、※

Z變換方法(P43)例：指數函數的Z變換。9.3

Z變換理論---1.級數求和法實例演示二、※

Z變換方法(P43)（1）

為得到閉合形式，上式兩邊分別乘以z-1

（2）

式（1）減式（2）得：例：求單位斜坡函數x(t)=t

的Z變換。9.3

Z變換理論---1.級數求和法實例演示二、※

Z變換方法(P43)常見函數的Z變換(P45表2.3)

⑴⑵⑶⑷⑸⑹9.3

Z變換理論二、※

Z變換方法Z變換方法1.※級數求和法2.※部分分式法（P44）3.留數法（補充）

先求出已知連續時間函數的拉氏變換；將展成部分分式之和的形式；查表對各部分分式分別求取Z變換，即得。9.3

Z變換理論----一般適用于E(s)沒有重極點的情況主要步驟：二、※

Z變換方法例2.7已知,試求相應的Z變換E(z)。解：將展成部分分式形式：對上式逐項取拉氏反變換，得：---2.部分分式法（P44查表法）9.3

Z變換理論二、※

Z變換方法也可直接Z變換Z變換方法1.※級數求和法2.※部分分式法3.留數法（P45）已知連續時間函數的拉氏變換及全部極點，其Z變換可由下面留數計算求得：式中：K—

的不相同極點的個數；

ri—極點si的階數；T—采樣周期。9.3

Z變換理論二、※

Z變換方法----一般適用于E(s)有重極點的情況例2.9：用留數法求單位斜坡函數的Z變換。解：拉氏變換式為顯然，只有一個二重極點，即s1

=0

，r1

=2，K=1。故：9.3

Z變換理論---3.留數法（P45）二、※

Z變換方法1.線性定理若，，，a為常數，則：三、Z變換的性質（P46)9.3

Z變換理論解釋：2.※※※實數位移定理（P46）7-2離散系統的數學基礎9.3

Z變換理論解釋：三、Z變換的性質（P46)如果函數e(t)是可拉氏變換的，其Z變換為

E(z)

，則有其中：k為正整數。滯后定理（負偏移定理）

：※超前定理（正偏移定理）

：2.※※※實數位移定理7-2離散系統的數學基礎9.3

Z變換理論2.※※※實數位移定理（P46）如果函數e(t)是可拉氏變換的，其Z變換為

E(z)

，則有其中：k為正整數。解釋：三、Z變換的性質（P46)滯后定理（負偏移定理）

：※超前定理（正偏移定理）

：（a）z-k環節的滯后作用（b）zk環節的超前作用9.3

Z變換理論結論：P47z-k代表時域中的滯后環節，它將采樣信號滯后k個采樣周期；zk代表超前環節，它把采樣信號超前k個采樣周期。2.※※※實數位移定理（P46）三、Z變換的性質（P46)演示例：用實數位移定理計算下列函數的Z變換：其中：a為常數。解：9.3

Z變換理論2.※※※實數位移定理（P46）三、Z變換的性質（P46)3.復數位移定理(48）

如果函數e(t)是可拉氏變換的，其Z變換為

E(z)

，則有9.3

Z變換理論解釋：三、Z變換的性質（P46)例：試用復數位移定理計算的Z變換。解：令e(t)=t

，則根據復數位移定理，有：9.3

Z變換理論3.復數位移定理(P48)三、Z變換的性質（P46)4.※※

※終值定理(P48)

如果函數e(t)的Z變換為E(z)，函數序列e(nT)(n=0,1,2,…)為有限值，且極限存在，則函數序列的終值(注：※若的極點均在Z平面單位圓內，則有上式成立）9.3

Z變換理論三、Z變換的性質（P46)例(2007)

已知試用終值定理計算x(nT)的終值。解：的2個極點在單位圓內，則由終值定理得：9.3

Z變換理論自測題三、Z變換的性質（P46)4.※※

※終值定理5.卷積定理

設x(nT)和y(nT)為兩個采樣函數，其離散卷積定義為：則若,必有卷積的Z變換7-3

Z變換理論解釋：三、Z變換的性質（P46)已知信號的Z變換表達式E(z)，求相應的離散序列e(nT)的過程。記為

注意：進行反變換時，信號序列仍是單邊的，即當n<0時，e(nT)=0。9.3

Z變換理論四、Z反變換（P50)Z反變換法冪級數法（長除法、綜合除法）2.※部分分式法（查表法）3.※反演積分法（留數法）9.3

Z變換理論四、Z反變換（P50)---1.冪級數法（長除法、綜合除法）將E(z)表示為按z-1升冪排列的兩個多項式之比：

直接作綜合除法，得到按z-1升冪排列的冪級數展開式：若此無窮冪級數收斂，則即為采樣脈沖序列的脈沖強度e(nT)。故脈沖序列表達式為主要思想（P50)9.3

Z變換理論四、Z反變換（P46)例2.14

用冪級數法求下列函數的Z反變換。解：將E(z)表示為:利用長除法得：則7-2離散系統的數學基礎9.3

Z變換理論---1.冪級數法（長除法、綜合除法）實例演示四、Z反變換（P46)實現步驟---2.※部分分式法（P51)（查表法）若E(z)無重極點，先將E(z)/z（P51）展開成部分分式之和：式中：是E(z)的極點；是是E(z)/z在極點zi處的留數。

將E(z)寫成部分分式之和：逐項查Z變換表得采樣瞬時序列：寫出已知E(z)對應的采樣函數：9.3

Z變換理論四、Z反變換（P45)例2.15

用部分分式法求下列函數的Z反變換。解：查Z變換表知采樣瞬時的信號序列則采樣函數9.3

Z變換理論---2.※部分分式法（查表法）四、Z反變換（P50)若部分分式使用不當，計算困難基本思想（P52)

已知連續函數e(t)的Z變換式為E(z)，可證明e(t)在t=nT時刻的采樣值e(nT)可由下面的反演積分計算:式中：zi

—E(z)zn-1的極點；

q—E(z)zn-1的不相同極點的個數；

ri—極點zi的階數。9.3

Z變換理論---3.※反演積分法（留數法）四、Z反變換（P43)有無重極點均可用留數法例：用留數計算法求下列函數的Z反變換。解：E(z)zn-1有兩個極點：。其階數分別為：

,不相同極點個數q=2；極點處的留數分別為：9.3

Z變換理論---3.反演積分法（留數法）四、Z反變換（P43)Z反變換法冪級數法（長除法、綜合除法）2.※部分分式法（查表法）3.※反演積分法（留數法）9.3

Z變換理論四、Z反變換（P46)回顧第9章線性離散系統的分析與校正9.1離散系統的基本概念

9.2信號的采樣與保持9.3Z變換理論9.4

※※線性離散控制系統的數學模型（描述）9.5※線性離散控制系統分析9.6※

※

線性離散控制系統的數字校正（設計）主要內容離散系統分析的數學基礎9.4離散系統的數學描述差分方程脈沖傳遞函數----時域----復域9.4離散系統的數學描述一、線性差分方程(P489)1.

差分定義前向差分1階前向差分2階前向差分n階前向差分后向差分1階后向差分2階后向差分n階后向差分演示e(kT)簡記為e(k)即：式中：和為常系數，2.線性常系數差分方程及其解法(P490)7-4離散系統的數學描述一、線性差分方程n階后向差分方程：n階前向差分方程：即：差分方程:離散系統輸入輸出變量及其各階差分的等式解法經典法（通解和特解）(不便）迭代法（遞推法）（了解）※Z變換法9.4離散系統的數學描述2.線性常系數差分方程及其解法(P490)一、線性差分方程9.4離散系統的數學描述2.線性常系數差分方程及其解法---迭代法一、線性差分方程(P490)例：已知其中，，。1）求當采樣時間T=1時的線性差分方程；2）試用迭代法求輸出序列c(k)，k=0,1,2,….得不到通式提示：①將差分方程變成前向差分方程；②根據Z變換實數位移定理的超前定理對差分方程逐項取Z變換，將差分方程的解C(z)表示成以z為變量的代數方程。注：計算中所需的c(k)初值個數應等于差分方程階數。③通過Z反變換求差分方程的時域解c(k)，推薦留數法。2.線性常系數差分方程及其解法---※

Z變換法9.4離散系統的數學描述一、線性差分方程

具體步驟(P490)：例：例9.4

：已知系統差分方程、初始狀態和r(k)如下：試用Z變換法計算輸出序列c(k)，k≥0。解：

①寫成前向差分方程：c(k+2)-5c(k+1)+6c(k)=r(k)9.4離散系統的數學描述一、線性差分方程2.線性常系數差分方程及其解法---※

Z變換法演示9.4離散系統的數學描述一、線性差分方程2.線性常系數差分方程及其解法---※Z變換法演示可得通式解：③應用留數法例9.4

：已知系統差分方程、初始狀態和r(k)如下：試用Z變換法計算輸出序列c(k)，k≥0。P5389-3(1)用Z變換法求解差分方程輸出序列c(k)

,k≥0.已知9.4離散系統的數學描述一、線性差分方程作業題或線性連續系統線性離散系統拉氏變換Z變換Z傳遞函數

9.4離散系統的數學描述二、脈沖傳遞函數(※※※)傳遞函數脈沖傳遞函數在零初始條件下，系統輸出采樣信號的Z變換與輸入采樣信號的Z變換之比（

※

※在輸入端必須有采樣開關）。※線性定常離散系統的脈沖傳遞函數定義（P492）9.4離散系統的數學描述二、脈沖傳遞函數(※※※)實際的開環離散系統

開環離散系統虛設采樣開關2.脈沖傳遞函數的性質-----了解9.4離散系統的數學描述實際的開環離散系統

1)脈沖傳遞函數是關于z的復函數，只適用于線性定常離散系統2）※脈沖傳遞函數取決于系統或元件結構和參數，是系統固有屬性3）

脈沖傳遞函數是在零初始條件下進行的二、脈沖傳遞函數(※※※)2.脈沖傳遞函數的性質-----了解9.4離散系統的數學描述實際的開環離散系統

4)系統脈沖傳遞函數=單位脈沖響應序列c(nT)的Z變換P4935)脈沖傳遞函數G(z)與差分方程的關系二、脈沖傳遞函數(※※※)1)定義法(復雜):

根據其傳遞函數G(s),求取其單位脈沖響應序列c(nT)的Z變換從而求得。3.脈沖傳遞函數求法9.4離散系統的數學描述實際的開環離散系統

二、脈沖傳遞函數(※※※)2)※直接法:直接根據其傳遞函數G(s)的Z變換得到G(z)

。即9.4離散系統的數學描述3.脈沖傳遞函數求法實際的開環離散系統

二、脈沖傳遞函數(※※※)有串聯環節時的開環系統脈沖傳遞函數；有零階保持器時的開環系統脈沖傳遞函數（※）有并聯環節時的開環系統脈沖傳遞函數（補充）

4.開環系統脈沖傳遞函數

9.4離散系統的數學描述注意：環節之間有無采樣開關及開關位置。二、脈沖傳遞函數(※※※)1）串聯環節之間有采樣開關開環系統脈沖傳遞函數:

等效離散系統4.開環系統脈沖傳遞函數（P494)---

9.4離散系統的數學描述串聯相乘

二、脈沖傳遞函數(※※※)開環系統脈沖傳遞函數為：2）串聯環節之間無采樣開關9.4離散系統的數學描述等效離散系統4.開環系統脈沖傳遞函數（P494)---

先相乘后離散

二、脈沖傳遞函數(※※※)例9.8：設開環離散系統如圖。其中：，求系統的脈沖傳遞函數G(z)。4.開環系統脈沖傳遞函數9.4離散系統的數學描述2）1）二、脈沖傳遞函數(※※※)3)有零階保持器時（※）含有零階保持器的開環離散系統等效開環系統4.開環系統脈沖傳遞函數---9.4離散系統的數學描述1二、脈沖傳遞函數(※※※)例9.9：設離散系統如圖9.17。已知：求系統的脈沖傳遞函數G(z)。3)有零階保持器時（※）4.開環系統脈沖傳遞函數---9.4離散系統的數學描述二、脈沖傳遞函數(※※※)并聯環節的開環離散系統開環系統脈沖傳遞函數:等效離散系統結構圖4)有并聯環節時（P496）4.開環系統脈沖傳遞函數---9.4離散系統的數學描述并聯相加

二、脈沖傳遞函數(※※※)對偏差信號進行采樣的系統可求得系統閉環脈沖傳遞函數

偏差脈沖傳遞函數只能求出系統輸出采樣信號的Z變換C(z)不對偏差信號進行采樣的系統5.※閉環系統脈沖傳遞函數(P497)---根據采樣開關實際情況具體分析9.4離散系統的數學描述二、脈沖傳遞函數(※※※)1)對偏差信號進行采樣的系統9.4離散系統的數學描述5.※閉環系統脈沖傳遞函數(P497)從系統輸出端入手，根據采樣開關位置和信號間傳輸關系列寫二、脈沖傳遞函數(※※※)法1：從系統輸出C(s)入手建立起各信號間拉式變換關系式；通過離散化和消去中間變量推導出C*(s)和R*(s)的關系式；通過Z變換導出C(z)或。圖9.22典型離散控制系統結構圖對偏差信號進行采樣的離散系統其閉環脈沖傳遞函數與連續系統的閉環傳遞函數形式上很相似。但是特別注意

9.4離散系統的數學描述

閉環離散系統的特征方程：1)對偏差信號進行采樣的系統(P497)5(※)閉環系統脈沖傳遞函數---

對輸入量的偏差脈沖傳遞函數:

對輸入量的脈沖傳遞函數:二、脈沖傳遞函數(※※※)圖9.22典型離散控制系統結構圖1)對偏差信號進行采樣的系統9.4離散系統的數學描述5.※閉環系統脈沖傳遞函數(P497)從系統輸出端入手，根據采樣開關位置和信號間傳輸關系列寫二、脈沖傳遞函數(※※※)法2※

：直接從系統輸出C(z)入手建立起各信號間的Z變換關系式

；消去中間變量推導出C(z)或圖9.22典型離散控制系統結構圖9.4離散系統的數學描述1)對偏差信號進行采樣的系統(P341)5(※)閉環系統脈沖傳遞函數---

對輸入量的偏差脈沖傳遞函數:

對輸入量的脈沖傳遞函數:二、脈沖傳遞函數(※※※)

獨立環節：兩個采樣開關之間的環節。

把Mason公式中各環節間的傳遞函數變為各獨立環節的Z變換即可。例：設閉環離散系統結構圖如下圖所示試求閉環脈沖傳遞函數。9.4離散系統的數學描述1)對偏差信號進行采樣的系統5(※)閉環系統脈沖傳遞函數---你能直接說出答案嗎？練習題二、脈沖傳遞函數(※※※)R(z)R*(s)例：解：7-4離散系統的數學描述1)對偏差信號進行采樣的系統5(※)閉環系統脈沖傳遞函數---演示二、脈沖傳遞函數(※※※)Y(s)-R(s)C(s)G(s)H(s)Y(z)=GH(z)E(z)C(z)=G(z)E(z)E(z)=R(z)-Y(z)圖9.22

系統結構圖9.4離散系統的數學描述5(※)閉環系統脈沖傳遞函數的計算快速自測題二、脈沖傳遞函數(※※※)C(z)=G(z)E(z)E(z)=R(z)-Y(z)9.4離散系統的數學描述5(※)閉環系統脈沖傳遞函數的計算Y(s)-R(s)C(s)G(s)H(s)C*(s)P498例9.10的系統結構圖Y(z)=H(z)C(z)快速搶答題二、脈沖傳遞函數(※※※)9.4離散系統的數學描述2)不對偏差信號進行采樣的系統5(※)閉環系統脈沖傳遞函數---不對偏差信號進行采樣的離散系統，

R(z)不能獨立出來不能求出脈沖傳遞函數，只能求出系統輸出采樣信號的Z變換C(z)。Y(s)R(s)C(s)X*(s)-G1(s)G2(s)H(s)E(s)C*(s)X

(s)B(s)R(s)C(s)X*(s)-G1(s)G2(s)G1(s)

H(s)C*(s)X

(s)(a)P499圖9.24系統結構圖（b）等效結構圖二、脈沖傳遞函數(※※※)9.4離散系統的數學描述2)不對偏差信號進行采樣的系統5(※)閉環系統脈沖傳遞函數---B(s)R(s)C(s)X*(s)-G1(s)G2(s)G1(s)H(s)C*(s)X

(s)P499圖9.24等效結構圖Y(s)R(s)C(s)X*(s)-G1(s)G2(s)H(s)C*(s)X

(s)P499圖9.24系統結構圖你發現規律了嗎？二、脈沖傳遞函數(※※※)從輸出端入手，根據等效結構圖采樣開關位置和信號間傳輸關系列寫例：設閉環離散系統結構圖如圖所示。9.4離散系統的數學描述5(※)閉環系統脈沖傳遞函數的計算練習題你能直接說出答案嗎？試求其輸出采樣信號的Z變換函數C(z)。二、脈沖傳遞函數(※※※)解：法1:C(s)-C*(s)-C(z)法2：等效結構圖9.4離散系統的數學描述5(※)閉環系統脈沖傳遞函數的計算演示例：設閉環離散系統結構圖如圖所示。按其等效圖列寫：G(s)H(s)G(s)R(s)C(s)-二、脈沖傳遞函數(※※※)H(s)G1(s)G2(s)G3(s)Y(s)R(s)C(s)X1(s)-X2(s)例：9.4離散系統的數學描述5(※)閉環系統脈沖傳遞函數的計算快速自測題C(z)=G3(z)X2(z)；X2(z)=G2(z)X1(z)；X1(z)=RG1

(z)

-G3HG1(z)X2(z)G1(s)

H(s)G1(s)G2(s)G3(s)R(