1、中考數學經典大題1 . 已知在 ABC中，/ ABC=90° , AB=6, BC=8點Q是線段 AC上的一個動點，過點 Q作AC的垂線交線段 AB (如圖1)或線段AB的延長線(如圖2)于點P.(1)當點P在線段 AB上時，求證：APQACB;(2)當 PQB是等腰三角形時，求 AP的長.2 .如圖，對稱軸為？?= -1的拋物線y = ?為+ ?(?w 0)與？軸相交于 A、B兩點，其中 點A的坐標為(-3, 0).(1)求點B的坐標；(2)已知？?= 1, C為拋物線與y軸的交點.若點P是拋物線上第三象限內的點，是否存在點P,使得 &poc=4Sboc,若存在，求點 P的

2、坐標；若不存在，請說明理由.設點Q是線段AC上的動點，作 QDL?軸交拋物線于點 D,求線段QD長度的最大值.若M是？軸上方拋物線上的點，過點 M作MNL?軸于點N,若AMNO與OBC相似，求M點的坐標.3.如圖，已知在 那BP中，C是BP邊上一點，/ PAC=/ PBA,。是4ABC的外接圓，AD是。 O的直徑，且交BP于點E.(1)(2)(3)求證：PA是。的切線；過點C作CF1AD,垂足為點 F,延長 CF交AB于點G,若AG AB=12,求AC的長;在滿足(2)的條件下，若 AF: FD=1: 2, GF=1,求。O的半徑.4 .如圖，已知函數y= -?2+ 2?+ 3與坐標軸分別交于

3、 A、D、B三點，頂點為 C. (1)求 BAD的面積；1(2)點P是拋物線上一動點，是否存在點P,使SaABP=2冬ABC?若存在，求出點 P的坐標;Q,使得 DOQ與 ABC相似，如果存在，求出點 P的坐標，如若不存在，請說明理由； (3)在軸上是否存在一點 果不存在，請說明理由.(1)(2)(3) 的點5 .如圖，在平面直角坐標系中，四邊形 ABCD是以AB為直徑的OM的內接四邊形，點 A、B 在？軸上， MBC是邊長為2的等邊三角形。過點 M作直線自？軸垂直，交。M于點E,垂 足為點M,且點D平分？?？求過A、B、E三點的拋物線的解析式；求證：四邊形 AMCD是菱形；請問在拋物線上是否

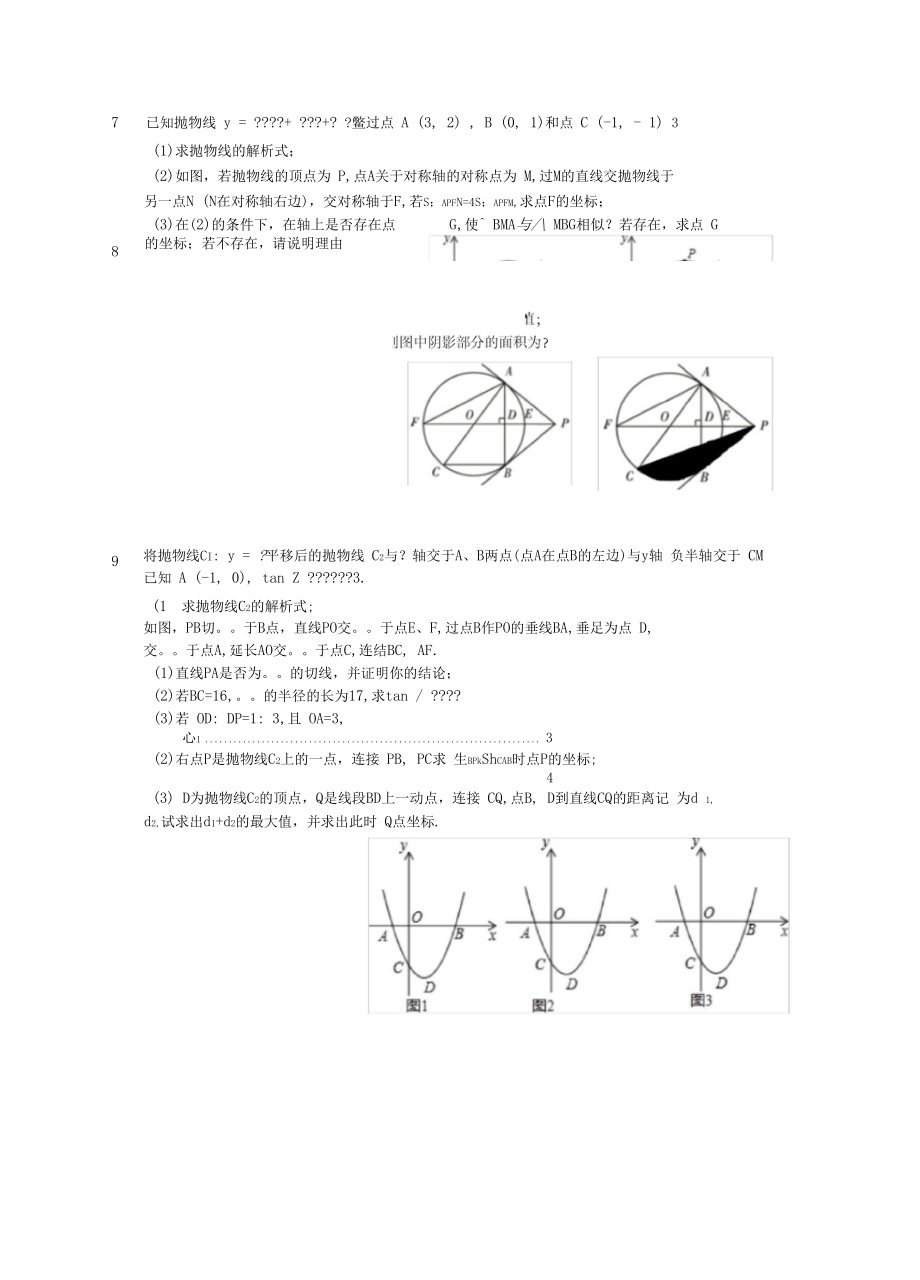
4、存在一點 P,使得 ABP的面積等于定值5?若存在，請求出所有P的坐標；若不存在，請說明理由6 . 如圖1,直角 ABC中，/ABC=90° , AB是。的直徑，。交AC于點D,取CB的中點E, DE的延長線與 AB的延長線交于點 P(1)求證：PD是。的切線;(2)若 OB=BR AD=6,求 BC 的長;F,若tan /C= 2,求二的值.?(3)如圖2,連接OD, AE相交于點7.已知拋物線 y = ?+ ?+? ?鱉過點 A (3, 2) , B (0, 1)和點 C (-1, - 1) 3(1)求拋物線的解析式；(2)如圖，若拋物線的頂點為 P,點A關于對稱軸的對稱點為 M

5、,過M的直線交拋物線于另一點N (N在對稱軸右邊)，交對稱軸于F,若S；apfN=4S；apfm,求點F的坐標；(3)在(2)的條件下，在軸上是否存在點G,使 BMA與/ MBG相似？若存在，求點 G的坐標；若不存在，請說明理由8.9.(1)求拋物線C2的解析式;將拋物線Ci: y = ?平移后的拋物線 C2與？軸交于A、B兩點(點A在點B的左邊)與y軸 負半軸交于 CM 已知 A (-1, 0), tan Z ?3.如圖，PB切。于B點，直線PO交。于點E、F,過點B作PO的垂線BA,垂足為點 D, 交。于點A,延長AO交。于點C,連結BC, AF.(1)直線PA是否為。的切線，并證明你的結

6、論；(2)若BC=16,。的半徑的長為17,求tan / ?(3)若 OD: DP=1: 3,且 OA=3,心1 3(2)右點P是拋物線C2上的一點，連接 PB, PC求 生BPkShcab時點P的坐標;4(3) D為拋物線C2的頂點，Q是線段BD上一動點，連接 CQ,點B, D到直線CQ的距離記 為d 1, d2,試求出d1+d2的最大值，并求出此時 Q點坐標.10.如圖1, AB為。的直徑，TA為。的切線，BT交。O于點D, TO交。于點C、E.(1)若 BD=TD,求證：AB=AT;(2)在(1)的條件下，求tan /?M;(3)如圖2,若？?=且。的半徑r=v7,則圖中陰影部分的面積為

7、？?311.如圖，過A (1, 0), B (3, 0)作？軸的垂線，分別交直線y = 4- ?F C、D兩點拋物線y = ?+ ?鱉過 O、C、D 三點.(1)求拋物線的表達式；(2)點M為直線OD上的一個動點，過 M作？軸的垂線交拋物線于點 N,問是否存在這樣 的點M,使得以A、C、M、N為頂點的四邊形為平行四邊形？若存在，求此時點 M的橫坐 標；若不存在，請說明理由；1(3)若點P為拋物線上的一點，連接 PD, PC.求 及PC吸&CDB時點P的坐標. 3(4)若 AOC沿CD方向平移(點C在線段CD上，且不與點 D重合)，在平移的過程中 AOC與 OBD重疊部分的面積記為 S,

8、試求S的最大值.i12.如圖，點C在以AB為直徑的OO±, AD與過點C的切線垂直，垂足為點 D, AD交。于 點E.(1)求證：AC平分/ DAB;.4, ?,(2)連接BE交AC于點F,若cos/?求一的值.5?13.如圖，在矩形 ABCD中，E是AB邊的中點，沿 EC對折矢I形ABCD,使B點落在點P處，折痕為EC,連結AP并延長交CD于F點.(1)求證：四邊形 AECF為平行四邊形；(2)若 AEP是等邊三角形，連結 B巳 求證： APB?EPG(3)若矩形 ABCD的邊AB=6, BC=4,求 CPF的面積.14.如圖，在平面直角坐標系 ？?為，拋物線y = ?- 2? 3

9、?(?< 0)與？軸交于A、B兩點 (點A在點B的左側)，經過點A的直線l: y = ? b與y軸負半軸交于點 C,與拋物線的 另一個交點為D,且CD=4AC.(1)直接寫出點 A的坐標，并求出直線l的函數表達式(其中 k、b用含？的式子表示)；(2)點E是直線l上方的拋物線上的動點，若ACE的面積的最大值為5,求？的值；4(3)設P是拋物線的對稱軸上的一點，點Q在拋物線上，以點 A、D、P、Q為頂點的四邊形能否成為矩形？若能，求出點P的坐標；若不能，請說明理由.15.如圖，已知 AB為。的直徑，PA與。相切于點A,線段OP與弦AC垂直并相交于點 D, OP與弧AC相交于點E,連接BC.

10、(1)求證：PA- BC=AB- CD.(2)若 PA=10, sin?3, 求 PE的長.516.已知：點P是平行四邊形 ABCD寸角線AC所在直線上的一個動點(點 P不與點A C重合)， 分別過點A C向直線BP作垂線，垂足分別為點 E、F,點。為AC的中點.(1)當點P與點。重合時如圖1,求證：OE=OF(2)直線BP繞點B逆時針方向旋轉，當/OFE=30時.若轉到如圖2的位置，線段 CF AE OE之間有一個不變的相等關系式，請寫出這個關系式.(不用證明)若轉到圖3的位置，猜想線段 CF AE OE之間有怎樣的數量關系？請予以證明 .17.已知如圖，在平面直角坐標系？?帆點A、B、C分

11、別為坐標軸上的三個點， 且OA=1, OB=2, OC=4.(1)求經過A、B、C三點的拋物線的解析式；(2)在平面直角坐標系？?州是否存在一點 P,使得以點A、B、C、P為頂點的四邊形為菱形？若存在，請求出點 P的坐標；若不存在，請說明理由；(3)若點M為該拋物線上一動點，在(2)的條件下，請求出當|PM-AM|為最大值時，點M的坐標，并直接寫出|PM -AM|的最大值.18.如圖，在RtABC中，Z C=90° , B葉分/ ABC DE 1BD交AB于E,。是4BDE的外接圓,交BC于點F.(1)求證：AC是。的切線；(2)連接 EF,若 BC=9,CA=12 求竺?值.5?1

12、9.如圖，在正方形 ABCM, AB=5,P是BC邊上任意一點，E是BC延長線上一點，連接 AP,作 PFLAP,使PF=PA連接CR AF, AF交CD邊于點G,連接PG.(1)求證：/ GCFh FCE;(2)判斷線段PQ PB與DG之間的數量關系，并證明你的結論；(3)若BP=2,在直線AB上是否存在一點 M使四邊形 DMPF平行四邊形，若存在，求出 BM的長度，若不存在，請說明理由 .20.1已知拋物線y = - 2?另+ ? c與y軸交于點 C,與？軸的兩個交點分別為 A(-4,0 ), B(1,0).(1)求拋物線的解析式；(2)已知點P在拋物線上，連接 PG PR若 PBC是以B

13、C為直角邊的直角三角形，求點 P 的坐標；(3)已知點E在？軸上，點F在拋物線上，是否存在以 A, C, E, F為頂點的四邊形是平行四邊形？若存在，請直接寫出點E的坐標；若不存在，請說明理由.21.如圖1,直角 ABC中，/ ABC=90 , AB是。的直徑，。交AC于點D,取CB的中點E, DE的延長線與 AB的延長線交于點 P.(1)求證：PD是。的切線；(2)如圖2,連接OD AE相交于點F,若tan/?2,求？?而值.?國;22 .已知四邊形 ABC皿菱形，AB=4, /ABC=60 , /EAF的兩邊分別與射線 CB, DCf交于點E,F,且/ EAF=60°(1)如圖1,當點E是線段CB的中點時，直接寫出線段 AE, EF, AF之間的數量關系;(2)如圖2,當點E是線段CB上任意一點時(點E不與B、C重合)，求證：