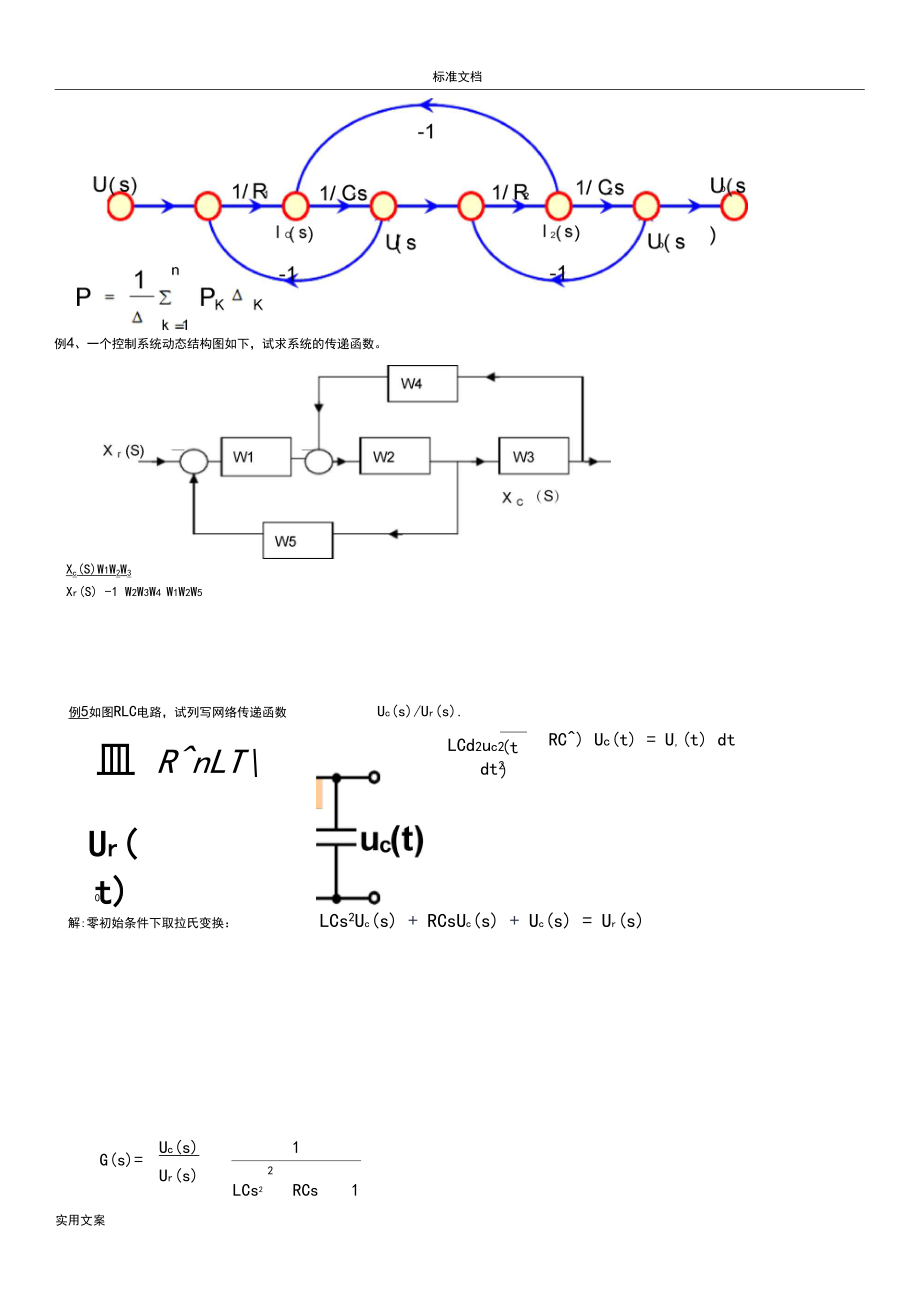
1、標準文檔第一章的概念1、典型的反饋控制系統基本組成框圖:復合控制方式。實用文案復合控制方式3、基本要求的提法：可以歸結為穩定性、準確性和快速性。第二章要求1、掌握運用拉氏變換解微分方程的方法；2、牢固掌握傳遞函數的概念、定義和性質;3、明確傳遞函數與微分方程之間的關系；4、能熟練地進行結構圖等效變換；5、明確結構圖與信號流圖之間的關系；6、熟練運用梅遜公式求系統的傳遞函數；Ci(s) C2(s)C2(s) G(S)_, _ _, _ _Ri(s) Ri(s)R2(s) R2(S)例1某一個控制系統動態結構圖如下，試分別求系統的傳遞函數Ci(s)Gi(s) C2(s)-GiG2G3Ri(s) -

2、 1 - GiG2G3G4 , Ri(s) - 1 - G£2G3G4例2某一個控制系統動態結構圖如下，試分別求系統的傳遞函數:C(s)Gi(s)G2(s)C(s)-G2(s)C(s) C(s) E(s) E(S)R(s) , N(s), R(s) , N(s)R(s) 1 G1(s)G2(s)H(s)N(s) 1 Gi(s)G2(s)H(s)例3:例4、一個控制系統動態結構圖如下，試求系統的傳遞函數。Xc(S)W1W2W3Xr(S) -1 W2W3W4 W1W2W5例5如圖RLC電路，試列寫網絡傳遞函數Uc(s)/Ur(s).皿 RnLTUr(t)LCd2uc2dt2(t)RC)

3、Uc(t) = U,(t) dt0解:零初始條件下取拉氏變換：LCs2Uc(s) + RCsUc(s) + Uc(s) = Ur(s)G(s)=Uc(s)Ur(s)12LCs2 RCs 1例6某一個控制系統的單位階躍響應為:C(t) =1 -2e+e,，試求系統的傳遞函數、微分方程和脈沖響應。-33s 2解：傳遞函數：G(s) =-3s上一(s 2)(s 1),微分方程：d-cn 3c9 2c(t) = 3dW 2r(t) dt2 dtdt脈沖響應：c(t) = -e' 4e't例Z一個控制系統的單位脈沖響應為C(t) =4e2 -e,，試求系統的傳遞函數、微分方程、單位階躍響

4、應。解：傳遞函數：G（s）3s 2,微分方程:(s 2)(s 1)d_cH 3dc( 2c(t) =3dr) 2r(t) dt2 dtdt單位階躍響應為:C(t) =1 -Ze? e上第三章本章要求：1、穩定性判斷1）正確理解系統穩定性概念及穩定的充要條件。 傳遞函數的極點均分布在平面的左半部。閉環系統特征方程的所有根均具有負實部；或者說，閉環2、3、1)2)3)2）熟練運用代數穩定判據判定系統穩定性，并進行分析計算。穩態誤差計算1）正確理解系統穩態誤差的概念及終值定理應用的限制條件。2）牢固掌握計算穩態誤差的一般方法。3）牢固掌握靜態誤差系數法及其應用的限制條件。動態性能指標計算掌握一階、二

5、階系統的數學模型和典型響應的特點。牢固掌握一階、二階系統特征參數及欠阻尼系統動態性能計算。掌握典型欠阻尼二階系統特征參數、極點位置與動態性能的關系。例1二階系統如圖所示，其中工=0.5,？=4（弧度/秒）當輸入信號為單位階躍信號時,試求系統的動態性能指標.解：；:=arctg = arctg 1(055 =60 =1.05(弧度)dtr"n7T-P- 2 =4 1 -0.52 =3.46-n.1 - 2346=0.60(秒)tpts3.5'-n3.50.5 4= 1.57(秒)A = 0.05crp=e100% =e_"二21 Q.52100% =16.3%ts4.

6、5- -n4.50.5 4= 2.14(秒)A = 0.02例3已知圖中Tm=0.2, K=5,求系統單位階躍響應指標。R(s)5?-(-)KS(TmS 1)C(s)解3:系統閉環傳遞函數為】（s）=G(s)1 G(s) - s(Tms 1) K化為標準形式中（s）=K/Tm222s2 s/Tm K/Tm s2 2 Ms . 一即有2 - n = 1/Tm=5,.n2=K/Tm=25解得Sn=5, t =0.5K23.5o%=e ” 父 100% = 16.3% ts = l=1.4秒 , n_n n n - P-tp = = 0.73 秒tr = = 0.486秒d -nJ- 2d例5:設控

7、制系統的開環傳遞函數系統為4s 5G=22s (s 2s 3),試用勞斯判據判別系統的穩定性，并確定在復平面的右半平面上特征根的數目。432解：特征方程：s 2s s 4s 5 = 0勞斯表控制系統不穩定，右半平面有兩個特征根。例6: 一個單位負反饋控制系統的開環傳遞函數為：G (S)=,要求系統閉環穩S(0.1S 1)(0.25S 1)定。試確定K的范圍(用勞斯判據)。解：特征方程：0.025s3 035s2 s K = 0勞斯表f0. 0251?K0. 35-0.025s 0.35系統穩定的K值范圍(0, 14)4 r 32例6：系統的特征方程：s 7 s 17 s 17 s 6 = 0解

8、：列出勞斯表：J 1176?71701 14.57 6- 14.12型別靜態誤差系數階躍輸入r(t) = R 1(t)斜坡輸入r(t) = Rt加速度輸入r(t)=Rt%VKpKvKat = R/(1 + Kp)ess = R Kvess = R Ka0K00R(1 + K)OOOOIOOK00RKOOnOOOOK00R KmOOOOOO0003 O因為勞斯表中第一列元素無符號變化，說明該系統特征方程沒有正實部根，所以：系統穩定。第四章根軌跡1、根軌埔方程 *K II (s - Zj ) j /nj (2 k 1)二 二e(k =0, -1,-2,)口 (s - Pi) i 1m * K i【

9、|s -Zj |二 1 n，i【I s - Pi I i 12、根軌跡繪制的基本法則mn“ (s- zj)八(s- pi) = (2k 1)二j =1i T3、廣義根軌跡(1)參數根軌跡(2)零度根軌跡XXXQ例1:某單位反饋系統,(1)(2)(3)實軸根軌跡(0,漸近線：3條。漸近線的夾角：3條根軌跡的起點為' Pi 一Zii 1i 1電=0 ( -1) ( -2)d= 一 1漸近線與實軸的交點:n - m(2k+ 1)兀(4) 得:(5)分離點:n - m二03-07t3,與虛軸的交點d1 -0.42, d2=-1.58 (舍去)系統的特征方程：1 . G(s)H(s)=0 即(s

10、3 3s2 2s K2 2j K = 02實部方程：一 3, K = 0虛部方程：一 3 . 2-=0解得:臨界穩定時的K=6o(舍去)2 2 +V2*K =6-0*K =0K為可變參數的根軌跡圖；由(1)根軌跡的起點為p1 =0, p2 = p3 =-0.5;終點為00(無開環有限零點)(2)根軌跡共有3支，連續且對稱于實軸;(3)根軌跡的漸近線有 n -m = 3條，(2k 1)二(- = 60 ,180 ;二 an -mPi0.33;(4)實軸上的根軌跡為0,-0.5=(-叼0.5;(5)分離點，其中分離角為 ±n /2 ,分離點滿足下列方程n 11'1-id d -

11、Pi dd 0.5例2已知負反饋系統閉環特征方程D(s) =s3 +s _0 +0.25K =0; + 0.25s+0.25K =0,試繪制以根軌跡圖確定系統臨界穩定時的K值;2s(s 0.5)解 特征方程D(s)=s3 +s2 +0.25s+0.25K =0得根軌跡方程為0.25K 1八，_斛方程得 d = 0 0.17；6(7)根軌跡與虛軸的交點：將 S = j。代入特征方程，可得實部方程為虛部方程為6 +0.25 6=0；.*2=35， K =1由根軌跡圖可得系統臨界穩定時K =1;由上述分析可得系統概略根軌跡如右圖所示：由根Ks(s 4)(s 6)(1)3條根軌跡的起點為P1 = 0,

12、 P2 = -4, P3 = -6;(2)漸近線：3條。漸近線的夾角:180 (2k 1)3-1=60 ,180(3)漸近線與實軸的交點:分離點：1 . _Jd d 4(0 4 6) - 03=0=一3.3332例3已知負反饋系統閉環特征萬程D(s)=s +10s +24s + K =0,試繪制以K為可變參數的根軌跡圖軌跡圖確定系統臨界穩定時的K值.32解特征方程D(s)=s +10s + 24s + K = 0得根軌跡方程為得 d1 = -1.57 (舍去)d2 = -5.1即 3d2 20d 24 =0(4)與虛軸的交點系統的特征方程：s(s+4)(s+6)+K *=0令S= j代入，求得

13、實部萬程：10，2 -K =0虛部方程： 3 -24 - 0解得： &=叫.9飛=0 (舍去)- /* *K =240K =0臨界穩定時的K =240'第五章 本章要求:1、正確理解頻率特性基本概念;設ui(t) =ASinmt ,貝U Ui(s) =Uo(s)=Ts 1As21 2匕小 A I-t/TAU0(t)=；2 re :2 2 Sin ( t - arctg T )1 .T12t2私、心、刀里" -t+ ：2 2其中： A(8)=1/U1 + 0 T ，中(6)= arctg c AuosSin ( t - arctg T); A A( ) sin t ()

14、,1 2T 2Cs(t) = AG(j8) sin8t + 邛 +/G(j8 )A3)= Gj)()二 G(j ) G(j y A( )ej ( )2、掌握開環頻率特性曲線的繪制；(1)開環幅相曲線的繪制方法1)確定開環幅相曲線的起點 缶=°林口終點81毛;2)確定開環幅相曲線與實軸的交點(-X , 0)Im G ( j x) H ( j ' x) 二°或 邛(0x)=/G(j0x)H(jM)=kn； k=°. ±1,±2,LLU6 x為穿越頻率，開環幅相曲線曲線與實軸交點為Re 'G ( j x)H ( j x)G ( j r

15、)H ( j x)3)開環幅相曲線的變化范圍(象限和單調性)。標準文檔(2)開環對數頻率特性曲線1)開環傳遞函數典型環節分解；2)確定一階環節、二階環節的交接頻率，將各交接頻率標注在半對數坐標圖的切 軸上；3)繪制低頻段漸近特性線：低頻特性的斜率取決于K /® ”還需確定該直線上的一點，可以采用以下三種方方法一：在0 < 8min范圍內，任選一點切0,計算：La(« 0 ) = 20 lg K - 20V 1g 0 0方法二：取頻率為特定值.0 =1,則La(1) = 201g K 1方法三：取La(，0)為特殊值0,則有K/；=1,即 0 = K"4)每兩

16、個相鄰交接頻率之間為直線，在每個交接頻率點處，斜率發生變化，變化規律取決于該交接頻率對應的典型環節的種類，如下表所示。3、熟練運用頻率域穩定判據；奈氏判據：反饋控制系統穩定的充分必要條件是閉合曲線r 包圍臨界點(-1,j0)點的圈數 R等于開環傳GH遞函數的正實部極點數 P。Z = P R= P 2N4、掌握穩定裕度的概念；相角裕度：系統開環頻率特性上幅值為 1時所對應的角頻率稱為幅值穿越頻率或截止頻率，記為 0，即CA3 c); Gj c)H j c) = 1定義相位裕度為=1800G(j c)H(j c)例1. G(s)=肅亍試繪制其 Ks(is )G(j加二加p解 |G(j«)

17、 |= j K2 21 T2- 2Nyquist 圖。/G(j ) u-90 - arctgT 0 |G(j)zG(j)=-90二 |G(j)|=0G(j)=-180G(j)/-j5U( ) =ReG(j) =-#V( ) =ImG(j)lim U( ) =*Tlim V( ) 二 0 >0Im"(kTjO) o 上例2. G(S)二S2(1 T1s)(1 T2S)解: G(j ')=|G(j ')產K/G(j ) =-180 -arctgT 樣：-arctg T2 1實用文案.二o |G(j J|- - G(j ) = -180二個 |G(j ') |

18、 = 0 G(j ) = -360 G(j ) = ReG(j -) ImG(j )標準文檔實用文案例3. G(S) =解：K(T1S 1)S(T2s 1)(丁2 Tl)K|G(j ) =co22T122丁2G(j )二 0=-90 arctgT 1 - arctgT 2G(j )G(j )卜二G(j - )= 0k(T -丁2)1 T2 2G(j ) = -90G(j ) = -90j K(1T1T22)(1 T2 2)lim U ( ) = K (T1 - T2)例4已知兩個費資饋控制系統的開環傳遞函數分別為：(1) G(s) =lim V ( )=試分別作出幅相頻靴性；并用奈奎斯特判據判

19、斷各系統的穩定性。一10(1) G(j 1)- - arctg 0.1 1arctg 2 1,0.01 2 1 . 4 2 1起點:終點:KOE)10Um(2) G(s) =(0.1s 1)(2s 1)'s(s 1)(2s 1)穿過負實軸：x 0 A(-x)=0 G(j )2j( . -2 .3) -3 .2-900 - arctg , - arctg 2起點:終點:穿過負實軸:0X -20x3 =0 , 0x1=f , A9x) 1 .332504例5已知單位負反饋控制系統的開環傳遞函數分別為：(1) G(s) = (2) G(s)= 試s(5s 1)s(s 1)(2s 1)分別作出

20、幅相頻特性；并用奈奎斯特判據判斷各系統的穩定性。一5050(1) (1) G(jco)=-=,N-90arctg 5j (j5 1)25 .2 1起點：終點：穿過負實軸:x =0 A( -x) = 0 G(j -)432j( -2 ) -3 d 900 - arctg,f：一arctg 2 1穿過負實軸:®x -2x3 =0,8x1=忑,A$x)=2.67例3最小相位控制系統的開環對數幅頻特性如圖所示。試求開環傳遞函數G (S)。K( 1)傳遞函數：G(s)=s2( 1)' 12K在低頻段有LaQ，)=20lg = =co40 =20lg K = K =100所以系統開環傳遞

21、函數為100(0.25s 1)s2(0.01s 1)例4最小相位控制系統的開環對數幅頻特性如圖所示。試求開環傳遞函數 制系統的穩態誤差。G (S);并求單位斜坡函數輸入時閉環控G(s)=K(0.1s 1)s(0.25s 1)(0.01s 1)20lg K =60 .K =100 0Kv1 =0.0011000第六章本章要求：1、掌握常用校正裝置的頻率特性及其作用；2、掌握選擇校正裝置的方法；3、重點掌握串聯校正設計方法；4、了解反饋校正、復合校正的設計方法；目前工程實踐中常用的校正方式有串聯校正、反饋校正和復合校正三種。例1: 一個單位負反饋系統其開環傳遞函數為G(s) =-100,要求相位裕量不小于 50° ,校正后的0 ：2 = 46.3 ,s(0.1s 1)試確定系統的串聯超前校正裝置。、100解：G(s)=/c” 一、作伯德圖,s(0.1s 1)c = 31.6, ( c) = 17.5°0( =4.