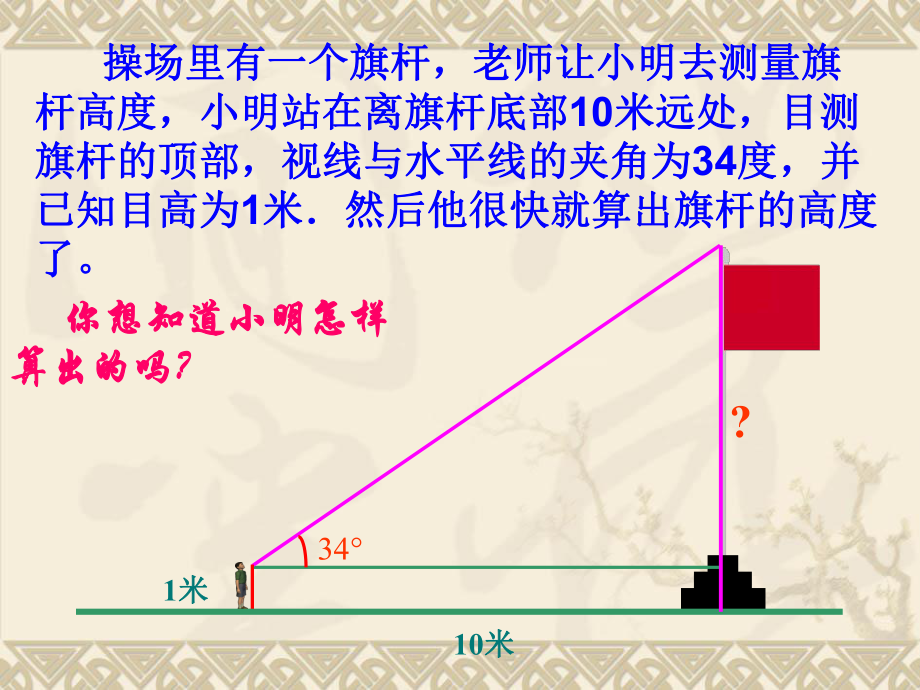
1、 操場里有一個旗桿，老師讓小明去測量旗操場里有一個旗桿，老師讓小明去測量旗桿高度，小明站在離旗桿底部桿高度，小明站在離旗桿底部10米遠處，目測米遠處，目測旗桿的頂部，視線與水平線的夾角為旗桿的頂部，視線與水平線的夾角為34度，并度，并已知目高為已知目高為1米然后他很快就算出旗桿的高度米然后他很快就算出旗桿的高度了。了。1米米3410米米? 你想知道小明怎樣你想知道小明怎樣算出的嗎？算出的嗎？我們已經知道，我們已經知道，直角三角形直角三角形ABC可以簡可以簡記為記為RtABC，直角，直角C所對的邊所對的邊AB稱稱為斜邊，用為斜邊，用c表示，另兩條直角邊分別叫表示，另兩條直角邊分別叫A的對邊與鄰邊

2、的對邊與鄰邊，用，用a、b表示表示.圖 19.3.1 如圖，在如圖，在RtMNP中，中，N90.P的對邊是的對邊是_,P的鄰邊是的鄰邊是_;M的對邊是的對邊是_,M的鄰邊是的鄰邊是_;（第 1 題） MNPNPN MN想一想想一想：P的對邊、鄰邊與M的對邊、鄰邊有什么關系？v觀察圖觀察圖19.3.2中的中的RtAB1C1、RtAB2C2和和RtAB3C3，它們之間有什么關系？它們之間有什么關系？圖 19.3.2 RtAB1C1RtAB2C2RtAB3C3所以所以_=_.111ACCB可見，在可見，在RtABC中，對于銳角中，對于銳角A的每一個的每一個確定的值，其確定的值，其對邊與鄰邊的比值是惟

3、一確定對邊與鄰邊的比值是惟一確定的的.B2C2AC2B3C3AC3圖 19.3.2 想一想想一想對于銳角對于銳角A的每一個確定的值，其對的每一個確定的值，其對邊與斜邊、鄰邊與斜邊、鄰邊與對邊邊與斜邊、鄰邊與斜邊、鄰邊與對邊的比值也是惟一確定的的比值也是惟一確定的 嗎？嗎？這幾個比值都是銳角這幾個比值都是銳角A的函數，記的函數，記作作sin A、cos A、tan A、cot A，即即 sin A= 斜邊的對邊Acos A= 斜邊的鄰邊Atan A= 的鄰邊的對邊AA cot A= 的對邊的鄰邊AA分別叫做銳角分別叫做銳角A的的正弦、余弦、正切、余切正弦、余弦、正切、余切，統稱為銳角統稱為銳角A

4、的三角函數的三角函數.1、sinA 不是一個角 2、sinA不是 sin與A的乘積 3、 sinA 是一個比值 4、sinA 沒有單位w由感性知識上升到理性知識由感性知識上升到理性知識: :w在在RtRtABCABC中中, ,sinAsinA和和cosBcosB有什么關系有什么關系? ? tanAtanA和和cotBcotB有有什么關系什么關系? ?互余兩角之間的三角函數關系w直角三角形直角三角形兩銳角互余兩銳角互余: :A+B=90A+B=900 0. . 回顧與思考回顧與思考駛向勝利的彼岸bABCacsinA=cosBsinA=cosB或或cosA=sinBcosA=sinB. .,sin

5、caA,coscbA,tanbaA.cotabA,sincbB ,coscaB ,tanabB .cotbaB tanA=cotBtanA=cotB或或cotA=tanBcotA=tanB. .w一個銳角的正弦一個銳角的正弦, ,等于它的余角的余弦等于它的余角的余弦( (或一個銳角的余弦等于它的余角的正或一個銳角的余弦等于它的余角的正 弦弦); );互余兩角之間的三角函數關系w結合圖形結合圖形, ,將將sinA=cosBsinA=cosB或或cosA=sinBcosA=sinB. . tanA=cotBtanA=cotB或或cotA=tanBcotA=tanB. .分別用文字語言敘述出來分別用

6、文字語言敘述出來: : 回顧與思考回顧與思考駛向勝利的彼岸bABCac,sincaA,coscbA,tanbaA.cotabA,sincbB ,coscaB ,tanabB .cotbaB w 一個銳角的正切一個銳角的正切, ,等于它的余角的余切等于它的余角的余切( (或一個銳角的余切等于它的余角的正切或一個銳角的余切等于它的余角的正切); );w一個銳角的正弦一個銳角的正弦, ,等于它的余角的余弦等于它的余角的余弦( (或一個銳角的余或一個銳角的余弦等于它的余角的正弦弦等于它的余角的正弦); );互余兩角之間的三角函數關系w一般地一般地,的余角為的余角為90900 0-,-,即即和和9090

7、0 0- -角互為余角角互為余角. . 回顧與思考回顧與思考駛向勝利的彼岸:因此更一般地有w一個銳角的正切一個銳角的正切, ,等于它的余角的余切等于它的余角的余切( (或一個銳角的余或一個銳角的余切等于它的余角的正切切等于它的余角的正切); );,cos90sin0,sin90cos0,cot90tan0,tan90cot0理解定義：理解定義： v1、你認為、你認為A的正弦、余弦的定義有什么區的正弦、余弦的定義有什么區別？正切、余切呢？別？正切、余切呢？v2、你能利用直角三角形的三邊關系得到、你能利用直角三角形的三邊關系得到sinA與與 cosA的取值范圍嗎？的取值范圍嗎？0sin A1，0c

8、os A1 v3、tan A與與cot A之間有什么關系？之間有什么關系？tan Acot A=1 4. sin A與與cos A之間有什么關系？之間有什么關系？練一練練一練1.判斷對錯判斷對錯:A10m6mBC1) 如圖如圖 (1) sinA= （ ） (2)sinB= （ ） (3)sinA=0.6m （ ） (4)SinB=0.8 （ ）ABBCBCABsinAsinA是一個比值（注意比的順序），無單位；是一個比值（注意比的順序），無單位；2)如圖，如圖，sinA= （ ） BCAB練習：練習：1、下圖中ACB=90 ，CDAB指出指出A的對邊、鄰邊。ABCD2、1題中如果CD=5，AC=10，則sinACD= sin DCB= 例例3、如圖，在、如圖，在ABC中，中， AB=BC=5，sinA=4/5，求，求ABC 的面積。的面積。55CDBA練習練習：（1）在）在ABC中，中，B=90 ，BC=3，A