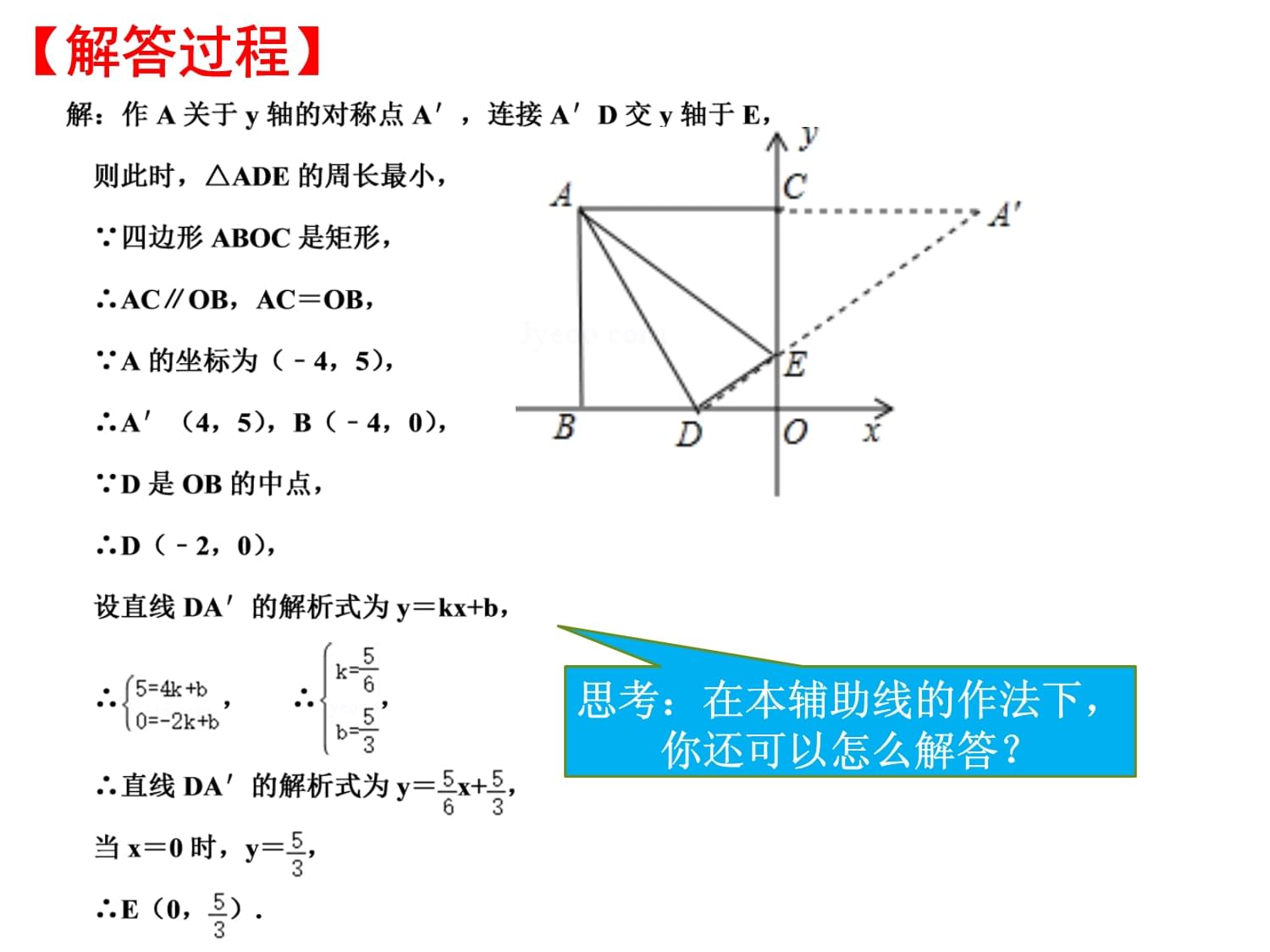
1、幾何中的最值問題學習目標：會利用四種基本模型求幾 何圖形中的最值.重點、難點：數學建模思想 和數學轉化思想.如圖，直線L同側有兩點，點A、點B，在直線L上求作一點P，使PA+PB最小. A L類型一：B PA軸對稱性質“將軍飲馬”線段垂直平分線兩點之間線段最短1、如圖，矩形ABOC的頂點A的坐標為（4，5），D是OB的中點，E是OC上的一點，當ADE的周長最小時，點E的坐標是 AE【跟蹤練習一】思考：在本輔助線的作法下，你還可以怎么解答？【解答過程】1、利用相似是解決問題的另一種常用方法； 2、多方法解決問題是專題復習中重點加強的.【解答過程】DE輔助線還可以怎么作？【跟蹤練習一】軸對稱性質【

2、跟蹤練習一】等邊三角形中將高線轉化為對稱軸，利用軸對稱的性質、兩點之間線段最短求線段和最小是解題關鍵。【解答過程】如圖，點A,B在直線L同側，在直線L上求作一點P,使 最大. A B L類型二：P根據三角形的兩邊之差小于第三邊，當A、B、P三點在同一條直線上時線段差最大，等于ABP1、在平面直角坐標系內有兩點A（1,1）， B（2，7），點M為x軸上的一個動點，若要使MBMA的值最大，則點M的坐標為 線段差最大的問題，轉化為與軸對稱性質、三角形三邊關系和函數（或相似）的綜合應用三角形相似【跟蹤練習二】如圖，點P為O外一點，則點P到O的最大距離或最小距離 .類型三：圓外一點到圓的最小距離線段PA

3、的長度3cm線段PB的長度圓外一點到圓的最大距離PAOB1、如圖，在RtABC中，ACB90，ACBC=2，以BC為直徑的半圓交AB于點D，P是 上的一個動點，連接AP，則AP的最小值是 EP【跟蹤練習三】圓外一點到圓最短距離與勾股定理的綜合應用2、（18泰安中考）如圖，M的半徑為2，圓心M的坐標為（3，4），點P是M上的任意一點，PAPB，且PA、PB與x軸分別交于A、B兩點，若點A、點B關于原點O對稱，則AB的最小值為_. P圓外一點到圓的最小距離【跟蹤練習三】ABOxyMP根據直角三角形斜邊上的中線等于斜邊的一半得出AB取得最小值時點P的位置【解答過程】3、在矩形ABCD中，AB4，AD

4、6，E是AB邊的中點，F是線段BC上的動點，將EBF沿EF所在直線折疊得EBF，連接BD，則BD的最小值是_.B圓外一點與圓的最小距離【跟蹤練習三】圓外一點到圓的最短距離與折疊的性質和勾股定理的綜合運用【解答過程】如圖，P為直線L外一點，在L上求作一點A， 使PA最小. P L類型四：A垂線段最短1、正方形ABCD中，AB=4，點P是對角線AC上一點，PECD于E，PFAD于F, 點P在線段AC上運動（P不與A,C重合），則EF的最小值 PEF最小BP最小垂線段最短熟練掌握正方形和矩形的性質，垂線段最短是解決此問題的關鍵【跟蹤練習四】【跟蹤練習四】點P的運動軌跡是DEF的中位線P1P2，BP的

5、最小值轉化為直線外一點到直線的最短距離，即當BPP1P2時，PB取得最小值【跟蹤練習四 】類型五：綜合運用1、如圖，BAC30，M為AC上一點，AM2， 點P是AB上一個動點,PQAC,垂足為點Q, 則PMPQ的最小值為 _NQP軸對稱性質垂線段最短線段和最短問題與軸對稱性質、垂線段最短、三角函數綜合應用，正確確定P點的位置是解此類題的關鍵【解答過程】軸對稱性質與線段和最小的問題【跟蹤練習五】利用反比例函數圖象上點的坐標特征，與軸對稱性質、線段和最小值、勾股定理的綜合應用。【解答過程】軸對稱周長最小線段和最小【跟蹤練習五】拋物線的對稱軸與線段和最小的聯系與應用是解決此類問題的關鍵【解答過程】四種基本圖形ABPlPBOAAPl線段和的最小值線段差絕對值的最大值圓外一點到圓的最大距離、最小距離垂線段最短在