1、艾滋病療法的評價及療效的預測摘要艾滋病作為人類社會最嚴重的瘟疫z-,其治療效果一直以來都倍受世人的關注。 眾所周知，治療方案的評價是一項艱巨而復雜的任務，是一個系統工程。木文主要研究了如何根據不同療法的臨床表現，用數學模型來評價其治療效果的優 劣。為了定量地進行分析，我們首先對題給數據進行了有效統計，得出了在每個測試點, 不同療法的有效性比率，成功的把零散的純數據信息轉化為了療效指標。在第（1）問預測繼續治療的效果時，考慮到測試的次數較少且測量的時間間隔是 非等間距的，通過對諸多預測方法的比較，我們選擇對傳統的灰色模型進行改進，建立 了非等間隔灰色預測模型。成功的把非等時間間隔數列轉化為等時間

2、間隔序列，再進行 預測。得到的預測函數為：a（l）x 二-58959.203e -0-,039><10/,2 -589676.678（cd4 濃度升高人數比例的變化）a（l）x （0 = -1940.369e-°0357/712 - 2034.781（hiv 濃度減少人數比例的變化）利用這兩個式子就可以方便的對繼續治療的效果作進一步預測。得到的結論是，隨著治 療時間的延長，治療效果將越來越差，甚至出現直線下降。在評價不同療法的優劣時，我們選擇層次分析法作為評價模型。首先通過對大量數 據的統計，基于對統計結果的深度分析，確定了特殊的評價準則：以數據口身的變化趨 勢制定評價指

3、標。接著建立了一種綜合考慮定量、定性指標的ahp模型，通過對傳統模 型的簡化改進，使計算求解過程更加簡潔方便。把該層次分析評價模型分別運用于第（2）問和第（3）問，得到的評價結果是：療 法4較優。我們借用了等時間間隔預測模型，得到了對該方法繼續治療的效果的預測。針對層次分析模型在人分析和思考時的模糊性，我們在模型的后續討論中進行了改 進，將模糊判斷矩陣轉化為精確矩陣，使層次分析法的計算方法得到了改進。關鍵詞：艾滋病，非等間隔灰色預測模型，層次分析法，預測模型transcripiionrna dma jhrovifut （circular strocluriiintergrasematurnt

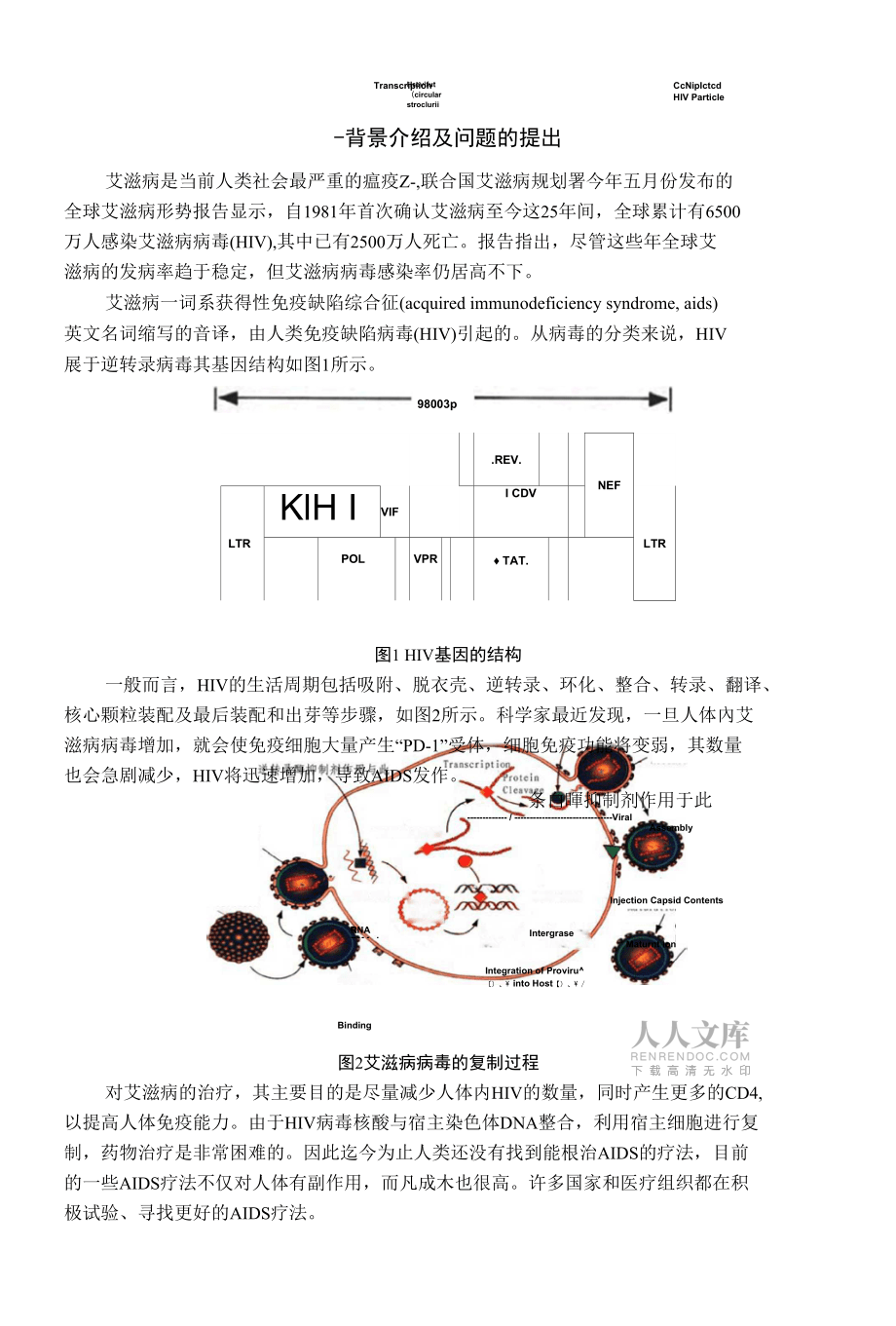
4、ionintegration of proviru）、 into host【）、 /ccnipictcd hiv particle-背景介紹及問題的提出艾滋病是當前人類社會最嚴重的瘟疫z-,聯合國艾滋病規劃署今年五月份發布的 全球艾滋病形勢報告顯示，自1981年首次確認艾滋病至今這25年間，全球累計有6500 萬人感染艾滋病病毒(hiv),其中已有2500萬人死亡。報告指出，盡管這些年全球艾 滋病的發病率趨于穩定，但艾滋病病毒感染率仍居高不下。艾滋病一詞系獲得性免疫缺陷綜合征(acquired immunodeficiency syndrome, aids) 英文名詞縮寫的音譯，由人類免疫缺陷

5、病毒(hiv)引起的。從病毒的分類來說，hiv 展于逆轉錄病毒其基因結構如圖1所示。.rev.nefltrklh ivifi cdvltrpolvpr tat.98003p圖1 hiv基因的結構一般而言，hiv的生活周期包括吸附、脫衣殼、逆轉錄、環化、整合、轉錄、翻譯、 核心顆粒裝配及最后裝配和出芽等步驟，如圖2所示。科學家最近發現，一旦人體內艾 滋病病毒增加，就會使免疫細胞大量產生“pd-1”受體，細胞免疫功能將變弱，其數量 也會急劇減少，hiv將迅速增加，導致aids發作。條白暉抑制劑作用于此 /viralassemblyinjection capsid contentsbinding圖2

6、艾滋病病毒的復制過程對艾滋病的治療，其主要目的是盡量減少人體內hiv的數量，同時產生更多的cd4, 以提高人體免疫能力。由于hiv病毒核酸與宿主染色體dna整合，利用宿主細胞進行復 制，藥物治療是非常困難的。因此迄今為止人類還沒有找到能根治aids的療法，目前 的一些aids療法不僅對人體有副作用，而凡成木也很高。許多國家和醫療組織都在積 極試驗、尋找更好的aids療法。為了對不同療法的效果進行比較，以便找到更好的治療方案，以下問題需要研究討論:（1）利用附件1的數據，預測繼續治療的效果，或者確定最佳治療終止吋間（2）利用附件2的數據，評價4種療法的優劣（僅以cd4為標準），并對較優的療 法預

7、測繼續治療的效果，或者確定最佳治療終止吋間。（3）如果病人需要考慮4種療法的費用，對（2）中的評價和預測（或者提前終止） 有什么改變。基本假設1、研究發現，當不同的人采取同一種治療方案時，其結果可能相差很大。但由于 參加試驗的人是隨即選取的，我們可以假設經過大量試驗后，試驗結果基本可以反映出 此種治療方案的效果。2、n前艾滋病的檢測主要是通過血檢和尿檢。由于實驗設備和檢測技術的原因， 檢測的結果往往有誤差。但附件小給出的數據是通過大量多次的檢驗而得到的，故我們 可以認為其是基本準確的。3、一般來說，受試者的年齡對治療效果有一定的影響。但在附件（2）中，由于分 組是隨機的，故可以不考慮年齡對治療

8、效果的影響。三 問題的分析及模型的準備通過簡單的分析可知道，本問題是一個藥物療效評價問題。不同治療方案的療效評 價是一項艱巨而復雜的任務，是一個系統工程。這里我們耍從藥物的臨床療效，來確定 它的有效性和安全性。由于參加每種試驗的人數是龐犬的和隨機選取的，如果耍對每一 個人的治療效果一一進行評價和預測顯然是相當麻煩的，而h醫學研究表明這也是沒有 意義的一一科研人員早就發現當不同的人采取同一種治療方案時，其結果可能相差很 大。這就提醒我們要對數據的整體進行分析，而不是單個分析。在問題（1）中耍預測繼續治療的效果，仔細分析附件一中的數據我們發現，雖然 每個人測試cd4和htv濃度的時間間隔是不同的，

9、但它們大體上分布在相同的時間段： 0周、4周、8周、25周、40周。故可以取這幾個吋刻作為參考點，分析在參考點 及附近，該療法對艾滋病患者cd4和hiv的濃度的影響。鑒于測試數據量較人，我們提 出鄰近原則對測試每個人的各次測量進行劃分：鄰近點：對各個實際測試吋刻與參考吋刻的作差比較，定義與參考點差值最小的時 刻為該參考點的鄰近點。鄰近原則：某個參考點的鄰近點性質特征近似于該參考點。靠近哪個參考點就用哪 個參考點代表。這樣，我們就把不同人的測試吋間統一到相同的幾個吋刻上。分析藥物對患者cd4和htv的濃度的影響，主耍從htv濃度的降低和cd4濃度的升 高來評價藥物的有效性。通過統計在藥物的作用下

10、，cd4和hiv的濃度升高和降低的人 數，得到藥物作用的有效率。利用得到的有效率，再建立數學模型對繼續治療的效果進 行預測。考慮到統計后的數據比較少，如果用一般的預測方法誤差將會很犬。考慮到灰色預 測模型具有所需樣本數據少、不要求典型的概率分布等特點，可以用它來進行預測。然 而傳統的灰色系統模型gm(1, 1)是以等間隔數列為基礎的，附件一中測量數據的吋間間 隔并不規則，呈現出非等間隔的狀態。所以我們需要對灰色模型進行改進，以便它能處 理非等間隔問題。問題(2)要求我們以cd4濃度為標準對四種治療方法進行評價，并選岀較優的治 療方法預測繼續治療的效果。由于病人的分組是隨即的，用不同療法的病人的

11、年齡分布 應該是相同的，從圖3我們可以看出年齡的分布基本上服從正態分布，故可以不去考慮 年齡因索對不同療法的影響。基于問題(1)中的討論，我們分別對用不同療法的病人 進行統計，統計的方法和問題(1)相同。由t cd4的濃度變化反映出不同療法的優劣, 我們可以選取每次測量時cd4濃度增加的人數比例作為準則，對不同療法進行判定。圖3年齡的止態分布檢驗層次分析法可以將決策者的經驗判斷給出量化，對缺乏必要數據的定性評價情況特 別適用，但它需要建立判斷矩陣，而客觀地建立判斷矩陣比較困難，并且受認為因素的 影響較大，得出的結論具有一定的主觀性。而在木題中，我們既要考慮定量指標(如不 同治療方案的效果)，乂

12、要考慮定性指標(價格因素)。為此，我們要提出一種綜合考慮 定量、定性指標的改進ahp模型。四非等間隔灰色預測模型的建立及問題1的求解由上面對問題的分析可知，我們需要建立非等間隔灰色預測模型。而傳統的等間隔 灰色gm (1, 1)模型是其基礎，故先介紹z。(-)傳統的灰色預測gm(l.l)模型：令x,(0)(/7)表示第i個原始數據。對一給定的幾將數列%/0)(/2)累加生成一新的數列w),其累加的原則是:兀=工兀®仗）（1 " s）7=1對兀建立如下形式的微分方程:式中q、勺在i不變吋是常數。進行離散化處理，處理的方法為:坷伙+1） 兀伙）伙+ l）_k=石伙+ 1）_兀伙

13、）=a（斥伙+ 1）表示儀dt用*（學）伙+ 1） +護伙）表示兀， 則離散化的結果為：a（兀伙+1）+* ©（兀伙+1）+兀伙）=m 為了解題的方便，記一扣（i）+兀）-（2）+兀）_(xo)(z?_l) + xa)(z2)1乙=（護（2），¥）（3）,護）丁, b嚴a，by o則上式可寫成矩陣的形式：y嚴xe記b為色的估計值，&為誤差，由最小二乘法原理，對&求最小值:2min ei 一 = min yi - x廠 s.可得:bj=（x：xjt（x：yj = （a,b）用估計值代替式（2）式小的系數，求解得：兀（"=（舌（0）_2）.g 一如+2

14、 aaj寫成離散形式，即為:兀伙+ 1)=(兀(1) _ 2) 嚴 +如a:a：此即為傳統的灰色預測模型，下面我們對它進行改進，建立非等間隔灰色預測模型。(二)灰色預測模型的改進非等間距灰色預測模型的建立:gm(1,1)模型是以等間隔數列為基礎的,但木題屮時間間隔并不是那么規則，而是呈現出非等間隔的狀態，這時，需要把非等間隔數列轉化為等間隔序列，再進行一次累加 生成處理，進而建立gm(1,1)模型。設有非等時間時隔數列= x(o)(l),x(o)(2),，兀其具體建模步驟如下：(1) 計算各觀測周期距首次周期的時間間隔這里，是各期的原始觀測時間。(2)求平均時間間隔i 川-1i求各期的時距與平

15、均時距的單位時間差系數求各期的總差值心)=心)1)式中?0)(0是對應的原始觀測值。計算等間隔點的灰數值嚴得到等間隔序列嚴=嚴4),嚴),/%)(6) 對嚴作一次累加生成(1-ag0)得円=円(1),円(2),#心)(7) 將z擬合成一階線性微分方程，即dzdt+az(,)a 按最小二乘法，由式(2)、(3)求解上式的待定參數a =得其時間響應函數a1 /z伙+1)=嚴ea還原為非等間隔數列屮與時間f有關的函數,%)= ?0)(1)-嚴7a人x(0)(0 = x (r)-x (-/() 這樣，將預測時間r代入上式，即可求得預測值。(三)模型的進一步改進非等間距灰色預測優化群的建立對所有的非間隔

16、數據可以按照模型上述進行建模。可以看出，其屮有一個過程是用 最小二乘法確定參數，這樣一來數據越多誤差就會越大，因為參數的個數沒有改變，述是 °川兩個;而且越來越多的研究表明用gm(1,1)模型來預測后續一段時間的數據,這段時 間間隔越小，就越準確，這段時間越長，準確性就越差；同樣，°m(1，1)模型真正有實際意 義的、精確度較高的用于預測的數據值，僅是最近的幾個對后續要預測的結果有實際意 義，很久以前的數據意義不是很大。基于此種原因，我們采用非等間隔數據gmd，l)模型 群的優化建模。思路如下：設有非等時間時隔數列x<°>=?o)(l),x(o)(2)

17、,，心),選擇最后的m + p個數據，其中m + p < n, p < m, p nj 以取 1,2,3 等,令：5(0)= |x(0)(/7 -77? - p +=嚴(1),嚴(2)，,嚴(加+ p)從s(°)屮選擇按加個數據一組，順序組成以卜5 + 1組非等間隔數據呼)=嚴,嚴(2),，嚴(訓 s畀)=嚴(2),嚴(3),，嚴伽+ 1)嚴(p + 1),嚴(p + 2),，嚴働+ p)對上述數據sf),s2®,s+f),分別采用模型1. 2進行求解參數這樣就得到：(q“),(21,2,p + l),然后用(q“)對嚴(加 + p)數據進行預測,這樣就得到p

18、+ 1個人(0)5/ (m + p),(心1,2,p +1),進而得到殘差:a«)込=si (7w + p)- 5<() (m + p)這樣就可以提出p+1個權值函數/i/(f 込/勺)j=i對所各模型預測得出的值進行加權，就得到了非等間隔數據gm (1,1)模型群的優化模型oa<°)"+1人(0)s (加 + 0 + g)二工/亂(m + 0 + g)f=l(四)模型的求解：利用問題的分析中的方法，統計服藥對艾滋病病人的cd4濃度影響:測試時刻(周)cd4升高人數cd4降低人數合計有效率(%)42925334584. 64824010334369.

19、972019110429564. 75401338822160. 18cd4濃度升高人數比例的計算步驟如下：(1) 計算各觀測周期距首次周期的吋間間隔(以周數為單-位)r. =0, 4,21,36, i二 1,2.4 (下同)(2) 計算平均時間隔心=占(36 0) = 12 (周)(3) 計算各期的時距與平均時距&()的單位時段差系數“s)= 0,-0.666667,0.25,0(4) 求各期的總差值心(°)(r.) = 0,9.777887,1.306273,0 計算等間隔點的灰數值?(,)(r,),得到等間隔的新數列z二84.63768, 60. 192963, 63.

20、439487, 60. 187(6)對z作一次累加生成(1-ago)，得z二84. 6376& 144. 830643, 208. 27013, 268.45013（7）對z擬合成一階線性微分方程”并按歸小二乘法求解，有-114.7341615 1_6092963一b=-176.5503865 1,y=63.439487_ -238.360131_60.18a =(brb)bty 解得0.0001039369028561.28916654248150（8）建立相應灰色微分方程的吋間響應函數a（l）x （it +1） = -5.895920302012144 x 105 x0000103

21、93690285a: -5.896766788 x io5（9）還原為非等間隔數列中與時間t有關的響應函數a （1）x （0 = -5.8959203 02012144 xlo5 xe 00（x）10393 690285 /7,2 -5.896766788 xlo5a（0）a（l）a（l）x t） x （f）i 兀（/ 12）根據以上模型對繼續服藥的有效性（以cd4濃度變化為評價依據）進行進一步預測結果 見下表：服藥吋間（周）cd4濃度升高人數比例（）5056. 886055. 937054. 978054. 029053. 0610052. 1111051. 1712050. 1913049

22、. 2414048. 2815047. 3316046. 3717045. 4218044. 4719043.5120042. 56服藥對艾滋病病人i1iv濃度的影響統計如卜表:測試時刻（周）hiv降低hiv升高合計有效率（%）43211934094.4182587533377.48252148630071. 33401197519461.34hiv濃度降低人數比例的計算步驟如門（1）計算各觀測周期距首次周期的時間間隔（以周數為單位）-二0,4, 21,36, i二 1,24 （下同）（2）計算平均時間隔a/（） = !（36-0） = 12 （周）4-1（3）計算各期的時距-與平均時距的單位

23、時段差系數“（心）=0,0.666667,0.25,0（4）求各期的總差值心（°） = 0,11.2895248,1.5360360375,0（5）計算等間隔點的灰數值得到等間隔的新數列z二94.41176471, 66. 18795268, 69. 7972972925, 61.34020619（6）對z作一次累加生成（1ago），得z（1） = 94. 41176471, 160.59971739, 230. 3970146825, 291. 7372208725 （7）對z擬合成一階線性微分方程”并按歸小二乘法求解，有< 127.50574111_ 66.18795268

24、 _b=-195.4983661,y=69.7972972925-261.0671178 161.34020619aa_ 0.03574561874891 _cl u72.73448302599449（8）建立相應灰色微分方程的吋間響應函數a （1）x 伙 + 1）二 1.940368596399637 xl（）3xe> -003574561874891' - 2.03478036 1109637 x 1（）3（9）還原為非等間隔數列中與時間沽關的響應函數a（l）% （r） =-1.940368596399637 xio3 003574561 874891/712 -2.0347

25、80361109637 xlo3a (0)a (i)a (1)兀(r) = x (r)-x (r-12)代入數據，得到繼續服藥的有效性(以hiv濃度變化為評價依據)的預測結果，見下表:服藥時間(周)hiv濃度降低人數比例()5061.576059. 76705&018056.319054. 6610053. 0511051.4912049. 981304& 5214047. 0915045.7116044. 3717043. 0718041. 8019040. 5820039. 39(五)對預測結果的分析:從上而預測的結杲我們可以看出，隨著時間的推移治療效果將越來越差，這充分地

26、 說明了艾滋病病毒的高變異性和高抗藥性，從一定程度上說明了艾滋病很難治療。圖4 cd4/iitv濃度隨時間的變化關系0k岸£阻咚05枚邕悝冬一h/k1。五 評價模型的建立及問題2和3的求解（-）基于層次分析法的評價模型的建立對于第二問我們采用層次分析法建模求解。層次分析法是美國著名運籌學家 l.saaty在二十世紀70年代中期提出用于決策和規劃的分析方法。它的基本思想是， 把復雜問題分解為各個組成因素，將這些因素按支配關系分組，形成不同層次。同一層 次的元素作為準則對卜層次的某些元素起支配作用，同時又受上一層次元素的支配。這 些層次大體上可以分為三類：1）目標層這一層次只有一個元素，

27、一般是分析問題的理想結果。2）準則層這一層次包括為實現目標所涉及的中間環節，它可以由若干個層次組成，包括所需考慮的準則、了準則。3）方案層表示為實現目標可供選擇的各種措施、決策方案等。這樣同層次元素間含義互不交叉，相鄰上下層元素間為上下級關系，形成遞階層次 結構，即評價指標體系。進而，以上一層元素為準則，將卜一層受其支配的元素進行兩兩比較，并把其相對 重要程度賦予一定數值而構成一個兩兩比較的判斷矩陣。如假設某一層個元素c,c2,.,ck對上一層一個元素o的影響，每次取兩個元素c, 和c/,用知表示g和q對的影響之比，全部比較結果可用成對比矩陣人=（知扁q >0叫=1/鶴由于上式給岀的知的

28、特點，人稱為正互反矩陣。其中g和cj對于上一層元素o的影響采用saaty等人提岀的1-9尺度（見下表），即知的取值范圍是1,2,9及其互為反數1,1/2,1/9。層次分析法中各尺度的不同含義：尺度知含義1g和c,的影響相同3g比的影響稍強5g比c,的影響強7g比的影響明顯的強9g比c,的影響絕對的強2, 4, 6, 8g和c；的影響之比在上述兩個相鄰等級之間1, 1/2,，1/9g和5的影響z比為上而勺的互反數另外，如果一個正互反矩陣4滿足% *aik =aik i,j,k = ,2,3,n則a稱為一致性矩陣，簡稱一致陣。容易證明斤階的一致陣a有下列性質1）a的秩為1, a的唯一非零特征根為；

29、2）4的任意一列向量都是對應于特征根的特征向量。再利用判斷矩陣4,根據根法，計算下層對于上層因素的相對重要性，即權重：叱= （上1,2,，n）工心1）=1然后，利用權重wi和止互反矩陣a的最大特征值入和，驗證矩陣a的一致性，一 致性指標ci為：n 一 1yauwjc其中，anax =-y-，隨機平均一致性指標ri查表得到，當比值指標c/?=<0.1n ,=i vv,.ri時，通過檢驗，否則對判斷矩陣進行修正，直到滿足條件為止。最后，合成方案層方案對于總目標的側度，其最終結果用權重表示。并對ci/cr值和權重向量3進行分析，將分析結果用于判斷和決策。傳統的層次分析法評價模型運用的基本步驟：

30、(1) 明確問題的性質和要求，提出總口標。(2) 建立層次結構。把問題分解為若干層次，第一層次為總目標，中間層可根據問題 的性質分解為不同層次，最低層一般為方案層或措施層。經過充分分析，畫出分層結構 圖。(3) 構造比較判斷矩陣。對同一層次內各因素，通過兩兩比較的方法，確定出相對于 上一層次各目標的權系數。設定當詢層次上的因索為4,相關的上一層因索為c,則可 針對c對所有a-進行兩兩對比得到相對重要程度知，這樣構成的矩陣的a稱為比較判 斷矩陣。其定義和解釋：記a的最大特征根,相對應的特征向量為 69 = (%02,©)"，則5為給出了因索4相對因索c的按重要程度的一個排 序

31、。(4) 求同一層次的組合權系數。設當前層次上的因素為4相對應的上一層c層因素為g,則當前層每個因索的權系數為：/=1如此類推，直到求出最低層一一方案層的權系數為止，并依次給出一個方案的優先程度 的定量化排序。一致性檢驗。計算得出的判斷矩陣a,有時可能會出現判斷上的不一致，因而要利用 一致性檢驗。其中ci = (2max -n)/(n-l)為一致性指標cr = ciiri為平均隨機一致性(ri 值參照值表)。當c/?<0.1時矩陣a通過一致性檢驗。否則，調整矩陣直到通過一 致性檢驗為止。(二)評價模型的求解：根據相關資料及分析需耍，對題中附件2所給數據作如卜統計分析: 療法1服藥時間(周

32、)cd4升高人數cd4降低人數合計有效率()87510918440.76087165211416631.325324479314033.57143325611216833.33333療法2服藥時間(周)cd4降低人數cd4升高人數合計有效率()815120035156.980061616714931647.15192411416928359.71731327214621866.97248療法3服藥時間（周）cd4升高人數cd4降低人數合計有效率（）815214629851.00671161649425863.56589241197()18962.9629632834512864.84375療法

33、4服藥時間（周）cd4升高人數cd4降低人數合計有效率（）87012419436.08247161157819359.5854924906115159.602653211956175684045196470. 3125總計有喩效 時s16243240140.7608731.325333.5714333.3333335.29412256.9800647.151959.7173147.151956.98006351.0067163.5658962.9629664.8437563.88889436.0824759.5854959.602656870.315為了便于分析數據，直觀反映數據變化特點，根據

34、上表，作曲線圖如下:亠療法一 療法二 亠療法三 十療法四圖5測試點數據變化趨勢圖從圖中可以很直觀的反映岀數據的變化特征，圖中系列號，分別代表各個不同的測 試點。通過對不同療法在各個測試點數據變化趨勢的分析，我們制定了療法選擇的決策 指標為：早期治療效果好，屮期效果平穩，后期效果上升三個正向指標，分別記為指標 1,扌旨標2,扌旨標3。現用以上建立的層次分析法評價模型對療效的選擇進行分析求解。stepl:建立遞階層次結構模型口標層g：選擇療法準則層s：指標1：早期治療效果好 指標2：中期治療效果平穩 指標3：后期效果上升方案層p：療法1,療法2,療法3,療法4 如下圖所示：step2:求第二層對第

35、一層的權向量：（1）構造成對比較陣：按照不同等級進行兩兩比較，通過對各因素的影響強度作定性分析，依據比較尺度, 按重要性等級，把3個指標進行兩兩比較得到評價矩陣（成對比較矩陣或正互反陣）:1 1/8 1/2_a= 8172 1/71"11/8m2列向量| 口一化>0.0910.0990.059-例：a =8170.7270.7800.82321/710.1820.1120.118（2）簡化法（和法）計算特征向量3,求權向量:按行 求和a0.249歸一化0.0832.3390.7800.4120.137_得到權向量:0.083q =0.7800.137step2:求第三層對第二層

36、的權向量:用同樣的方法構造第三層對第二層的每個指標的成對比較陣:712 _11/81/2_1 1/3'1/711/61/6,=,b3 =81931 _161221/911/261/211這些矩陣小的元素是各個方案（療法）對于準則層各個指標的優越性的比較尺度。step3:由第三層的成對比較陣bk計算出權值:0.1410.50.50.1050.1350.6180.081破）=0.8050.123結果列入下表中： 表：各次測量的權重k12340.50. 50. 1410. 1050. 1350.6180. 0810. 8050. 123step4: 致性檢驗通常檢驗的方法有兩種，分別為：方法

37、（1）用一致陣性質判定：1）a的秩為1, a的非零特征根為n；2）a的任一列向量都是對應丁特征根n的特征向量； 方法（2） 致性指標判定用一致性指標評價特征向量矩陣有無邏輯混亂。先算出特征值，然后代入求得一致 性指標ct的值,再查表得3個因素的隨機性指標cr值為0. 58。算出ct/cr的值,小 于0.1,則x的不一致性可接受，即評價因素的特征向量矩陣無邏輯錯誤。由于n值較小，所以用方法（1）判定更加方便。我們通過方法（1）驗證通過。通 過算岀ci/cr=0.018<0. 1,再次檢驗了 x的不一致性可接受，即評價因索的特征向量矩 陣無邏輯錯誤。stcp5:計算組合權向量0.141x0.

38、780 + 0.081x0.137 = 0210.105x 0.780 + 0.805 x 037 = 0.192035 x 0.780 + 0.5 x 0.083 = 0.1470.618x0.780 + 0.5 x 0.083 + 023x037 = 0.5400 = （0.121,0.192,0.147,0.540）根據檢驗原則，再次一致性檢驗結果，x的不一致性可接受。結論：療法4為較優療法。(三)預測用療法4繼續治療的效果：用問題(1)中等時間距預測模型進行預測如21) 據統計療法四的有效率為等吋距的數列兀二36. 08247, 59. 58549, 59. 60265, 68, 70

39、.3152) 對兀作一次累加生成(1-ag0),得x二36. 0824, 95.66789, 155. 27054, 223.27054, 293. 5833) 對兀擬合成一階線性微分方程并按最小二乘法求解，有-65.875145r"59.58549_-125.4692151,y=59.60265-189.27054168-258.42679170.3125 _由 a =(bi b)bry 解得a a卜 0.044728274'll u60.035362794) 得到相應灰色微分方程的時間響應函數a (i)x 伙 + 1) = 1378.30640 8 x 0()447282

40、7 41- - -1342.22400 8 a(l)5) 對兀伙+ 1)作累減生成，可得其還原值a (0)a (1)a (1)x (k + l)-x 伙+ 1) 一兀(k)根據以上模型對繼續按療法四服藥的有效性進行進一步預測結果見下表:服藥時間(周)有效性()4875.40110425678.850227096482.457125517286.229016688090.173447988894.298312039698.61186247預測數據與實際藥物耐藥性存在的事實有出入，但從整體趨勢中，可以看出，療法 4的藥性持久，療效較其他療法的確更優。(三)問題(3)的求解考慮4種療法的費用，相當于

41、在問題(2)的基礎上，往準則層中加入了一個新的 指標，如下圖所示：很顯然，新指標與原指標z間和對獨立。在該種情況下，比較尺度是基于藥品供應 商對不發達國家提供藥品的現實來確定的，藥品費用對患者做出療法選擇過程中產生了 較大的影響。與第二問求解過程類似，只是增加了一組數據。最后同樣可以由構造的幾 組成對比較陣求得相對權向量和組合權向量：(1) 求第二層的成對比較陣對第一層的權向量：181/811/271/91/2構造成對比較陣：a =a21/711/892810.039權向量:0.377(q > =0.0680.516(2) 第三層的成對比較陣對第二層的權向量: 構造成對比較陣：1/311

42、1/711/271661/611/221/621_11/81/5l/9_11/8l/2_8141/2819，乞=5411/621/911926105,洌 2)=_0.141_0.105，=_0.08f0.805，研）=_0.035_0.2820.50.1350.240一 0.1230.618jj0.443（3）對組合權向量計算處理，得到各個療法在目標中的組合權重:權向量：e；0 = (0 139,0.338,0.271,0.769)同樣進行組合一致性檢驗。檢驗通過。結論：療法4仍為較優療法。由題給數據我們知道，療法4雖然療效較好，但相對其他療法費用較高，而對于不 發達國家的人民來說，該結論的得

43、出與實際有一定的出入。這與我們的評價模型中涉及 到的人在分析和思考時的模糊性有關。我們嘗試著對模型進行改進。針對木文在考慮人在分析和思考時的模糊性。對判斷矩陣進行改進如下：具體評分 時，對于判斷矩陣4 =（知）切的元素勺，專家用三角模糊數標岀兩兩指標間的相互關系。 首先標岀最有可能值加表示對兩指標相互關系的基本評價，接著標出上下界q和方。下 界表示專家認為可能的最低評分，上界表示可能的最高評分，則指標i相對于指標/的 權重a(j = (a + 4m + /?) / 6j方井為a2 = (b_a)/6華羅庚教授曾對類似公式做過說明。知是最高評分或最低評分的可能性比較小，更 多的是最有可能值，近似

44、服從于止態分布。假定加的可能性2倍于a或b的可能性，應 用加權平均法。在（a,加）間的平均值為（a+ 2加）/3,在（加，方）間的平均值為（2加+方）/3 ,則分布可以用（a + 2加）/ 3與（2加+ b） / 3各以（1 / 2）可能性出現的分布來代表,clij =133)a + 4m + b6而方差"d + 4/77 + h2加 + b y63丿_i 6丿a + 2m y3；例如，某專家對指標1和指標2相對權重的評分是（2/3,1,3/2），則此專家對指標1相3 + 4x1 + ?對于指標2的權重評價為:知=o636模糊判斷矩陣轉化為精確矩陣后，改進的層次分析法的計算方法與前面

45、的分析模型和 同，在此不再贅述。六模型的優缺點及評價：（1）我們建立的模型既考慮了以往數據所包含的信息，乂考慮了最新數據所包含的 信息；（2）通過舊數據建立的灰色模型預測得到的預測結果，由于舊數據包含的對預測結 果影響的信息一般來說比較少，因而一般來說誤差也就較大，這個灰色模型就可以選用 較小的權值;相反比較新的數據建立的灰色模型所預測的結果，由于新數據包含的對預 測結果影響的信息一般來說比較大，因而一般來說誤差也就較小，這個灰色模型就可以 選用較大的權值。（3）模型的信息貢獻是由自身的精確度決定的。精確度高，貢獻就大；精確度低，貢 獻就小；這一點也反映了以往數據與預測結果是有相關性的。（4）

46、與傳統的灰色預測模型相比，我們建立的非等間隔灰色預測模型更適合本題， 在計算的精度上有了很大的提高。（5）在用層次分析法建立評價模型吋，我們選擇早期治療效果好，中期效果平穩， 后期效果上升三個指標作為評價的準則，很好地反映了不同療法的效果。但它們之間不 是絕對獨立的，將會給我們的評價帶來一定的謀差，這也是我們在進一步討論小要解決 的問題。七模型的進一步討論現實生活中許多評價問題都屬于多人、多層次和多目標綜合評價問題。目前廣泛應 用的層次分析法在建立判斷矩陣時，只是將各方案的單個指標值進行比較，沒有考慮指 標間的相互聯系。然而，一般情況下因索指標之間并不是相互獨立的。雖然它們之間的 關系不明確，但的確存在，從木質上講。因此，對于指標間關聯性比較強的評價體系來 說,ahp法并不是最佳評價方法。下面我們討論采用ahp法確定因索指標權值和灰色關聯度分析法建立決策矩陣，實現 對復雜產品方案的綜合評價。設決策論域 =wpw2,«,是方案集合，v =片川2，是評價指標集合，則由" 與v中任意搭配的元素對仏皿）構成關于刃個評價指標條件產品方案的笛卡爾乘積