2024年本溪市高級中學中考自招數學復習題

一.選擇題（共22小題）

1.如圖，在△4BC中，ZC=90°,C力_LAB于在（1）QC?A8=4C?8C；（2）—r=——：

BC2BD

111

（3）—+—=—;（4）AC+BOCD+AB中正確的個數是（）

AC2BC2CD2

2.設〃是正整數，OVxWl,在△ABC中，如果AB=〃+x,BC=n+2x,CA=〃+3x,BC邊

上的高4。=小那么，這樣的三角形共有（）

A.10個B.11個C.12個D.無窮多個

3.某輪船往返于A、8兩地之間，設船在靜水中的速度不變，那么，當水的流速增大時，

輪船往返一次所用的時間（）

A.不變B.增加

C.減少D.增加，減少都有可能

4.當x=l,y=-l時，ax+by-3=0,那么，當x=-l,y=1時，ax+by-3=（）

A.-6B.-5C.-4D.-3

5.已知/%?l=x，其中p,4為質數且均小于1000,x是奇數，那么x的最大值是（）

A.1991B.1992C.1993D.1994

6.P是凸四邊形內的一點，P與四個頂點連接得到的四條線段的長分別為1,2,3,4.那

么，這個四邊形的面積的最大值為（）

A.10.5B.12C.12.5D.15

7.我們對一些較大的數設計出一種簡單的記法：為〃個連續出現的4記為辦.其中〃是

正整數，”是一個一位整數（0W4W9）.例如93857462表示99988888777766.如果

2x3y52+3：5x2），=53835373,那么x,y,z的值分別是（）

A.4,5,3B.3,6,3C.3,5,4D.5,3,4

8.如圖，是一座建筑物的平面圖，其中的庭院有兩處供出入的門，過路的人可以在門外觀

看但不能進入庭院，圖中標明了該建筑物的尺寸（單位：米），所有的壁角都是直角，那

第1頁共46頁

么過路人看不到的門內庭院部分的面積是()

A.250B.300C.400D.325

9.如圖，△A8C中，AB>AC,AD,AE分別是其角平分線和中線，過點C作。G_L4)于

點F,交AB于點G,連接ER則①?ZBCG=1(ZACB-NA8C)；@EF=1

(AB-AC)：(AB-AC)(AB+AC).其中正確的是()

A

BEDC

A.①②@@B.(D@C.②③④D.?@?

10.某油漆專賣店，昨日進了“金魚”、“三葉”、“力王”三種品牌油漆，相同牌子的顏色相

同，不同牌子的顏色不同.已知蘭花白的每桶3千克，百合彩的每桶4千克，風鈴彩的

每桶5千克.為了方便顧客，將三種油漆都分裝成1千克的小桶，結果“金魚牌”油漆

裝了280桶，“三葉牌”油漆裝了255桶，“力王牌”油漆裝了292桶，則“金魚”、”三

葉”、“力王”三種油漆的顏色分別為()

A.風鈴彩、蘭花白、百合彩B.百合彩、蘭花白、風鈴彩

C.蘭花白、風鈴彩、百合彩D.蘭花白、風鈴彩、百合彩

11.小明在操場觀看投擲標槍，如圖是他看到的一次標槍飛行圖象，若按標槍飛行先后順序

將下列圖象排序，正確的是()

12.已知圖中三十六個小等邊三角形的面積都等于1,則三角形48c的面積為(

第2頁共46頁

C.23D.24

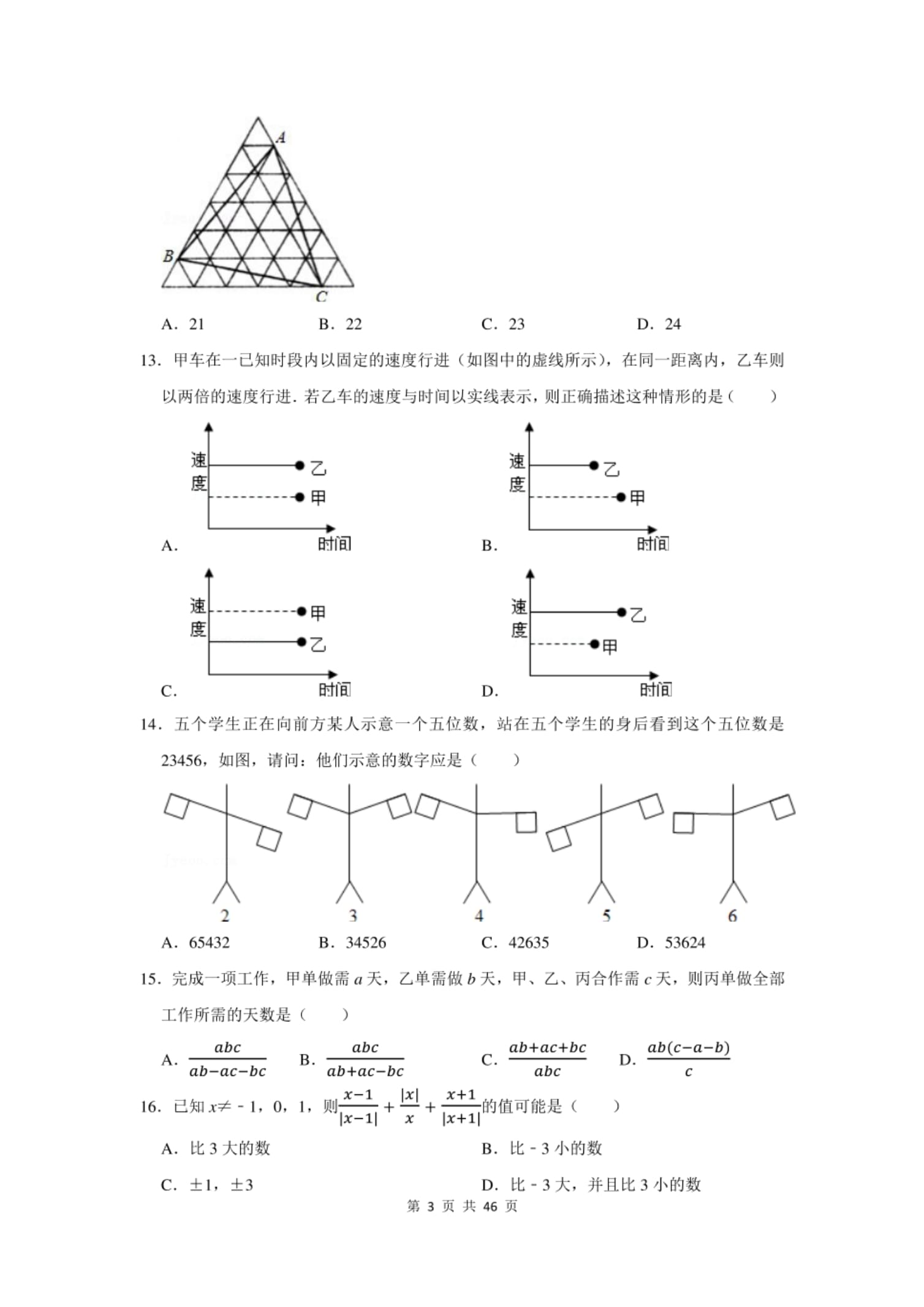
13.甲車在一已知時段內以固定的速度行進（如圖中的虛線所示），在同一距離內，乙車則

以兩倍的速度行進.若乙車的速度與時間以實線表示，則正確描述這種情形的是（）

14.五個學生正在向前方某人示意一個五位數，站在五個學牛.的身后看到這個五位數是

23456,如圖，請問：他們示意的數字應是（）

15.完成一項工作,甲單做需。天，乙單需做〃天，甲、乙、丙合作需c天，則丙單做全部

工作所需的天數是（）

abcabcab-{-ac+bc口ab(c-a-b)

A，ab-ac-bcB.----------------C.

ab+ac-bcabc

16.已知此7,。“則^+4+黑的值可能是（

)

A.比3大的數B.比-3小的數

C.±1,±3D.比?3大，并且比3小的數

第3頁共46頁

17.如圖，梯形ABCD中，A8〃CZZ兩條對角線交于點￡已知△ABE的面積是小叢CDE

的面積是。，則梯形ABCO的面積是（）

B.V2(a+b)C.(Va+V^)2D.Ca+b)

18.如圖，AB=BC,點。在BC上.以。為直角頂點作等腰直角△AQE,貝!當。

從B運動到。的過程中，點上的運動軌跡是（）

A.圓弧B.拋物線C.線段D.雙曲線

x1+x2+x3=%

y21y3iV4-n2f其中則XI，必

“3十“4十"1—a3

{工4++%2=a4

由，X4的大小關系是（）

A.Al<.r2<X3<X4B.X2<X3<X4<XI

C..V3<X2<XI<X4D.X4<X3<X2<AT1

20.已知2WRW3,則函數y=(x-1)2的取值范圍是()

A.1忘)，忘4和9W曠近16B.9W〉W16

C.4W)，W9D.lWyW9

21.如圖，已知梯形ABC/）中，AB//DC,ZA=a,ZC=p,則A。：BC等于（）

A.sina：cos0B.sina：sinpC.sin0：sinaD.cosa：sin0

22.若關于x的二次函數），=7-2〃LI+1的圖象與端點在（-1,1）和（3,4）的線段只有

一個交點，則〃?的值可能是（）

第4頁共46頁

二.填空題(共34小題)

2732>/3

23.化簡：五礪一西兩=——.

24.將x3?ax1-2ax+a2-1分解因式得.

25.若x,y是正整數且x+y+xy=34,則x+)，=.

26.已知實數x,y,z滿足x-y=8,xy+z2=-16?則/+y+z=.

27.已知平行四邊形48C。的周長為52,自頂點。作。DF±BC,E、尸為垂足，

若DE=5,DF=8,則的長為.

28.在算式ai+c+d+eW+g中，任意加括號來指出運算順序.例如((〃+〃)入)+

(d+e)+(f+g)

為其中一種方法.則所有可能添加括號的方法，一共可以得到種不同的運算結果.

29.如果關于x的方程中+的+尚=自有正整數解，那么正整數女的所有可能取值之

和為.

30.如圖，在等腰△ABC中，D,E分別是AB,AC上的點，滿足8D=CE,F是BE與CD

的交點.如果S四邊形4。b￡=48,S"C7：=18,那么S”BC=

31.用S(〃)表示正整數〃的各位數字之和.如果不相等的正整數。，8滿足S(a)+a=S

(b)+〃，那么。+人的最小值為.

32.如圖，在長方形48CD中，七是A3的中點，〃是4。的一個三等分點，FB與EC，ED

分別交于點G,H,FC與ED交于點、I.則:"小""=__________

,四邊形ABCD

第5頁共46頁

33.一粒米，在許多人看來是微不足道的，平時在餐桌上毫不經意掉下幾粒，也很少有人在

乎它.一粒米大約重0022克，我國現有人口13億，按每人每天三餐計算，如果每人每

餐掉一粒米，那么全國人民一年（按365天計算）大約浪費糧食千克.（要

求：用科學記數法表示）.

34.某廠承印新課程標準實驗教材，新書出廠時，要將打包成長、寬、高分別為x分米、y

分米、z分米的長方體包裝加上扎帶（如圖所示雙虛線位置）.若扎帶每個接頭處要多余

0.5分米，則一個長方體包裝上的扎帶總長分米.

35.在某小說里，有這樣一個故事情節：女盜“獨一枝”的助手麗卡溜進某億萬富翁家里，

找到了地下室的金柜.她知道，只要打開金柜，剩下的事就好辦了.有關金柜的密碼，“獨

一枝”是這樣告訴她的：“金柜上放著一本厚約500頁的書，有一書簽夾在書中，夾著書

簽的那兩頁書的頁碼和就是密碼”.若書簽可能夾在：①85頁?86頁之間；②413頁?414

頁之間；③420頁?421頁之間.則你認為金柜的密碼是.

36.甲、乙兩隊舉行拔河比賽，標志物先向乙隊方向移動0.2米，又向甲隊方向移動0.5米，

相持一會兒，又向乙隊方向移動0.4米，隨后又向甲隊方向移動1.3米，在大家的歡呼鼓

勵中，標志物又向甲隊移動0.9米，若規定標志物向某隊方向2米該隊即可獲勝，那么現

在隊贏了.

37.如圖是一個風景區，A,B,C,D,E,尸是這一風影區內的六個主要景點，現觀光者

聚于A點.假若你是導游，要帶領游客欣賞這六個景點后再回到4點，但又不想多走“冤

枉路”，你將選擇的行走路線為.（只需填一種即可）

第6頁共46頁

D

38.如圖，在一塊展示牌上，整齊地貼著許多資料卡片，這些卡片的大小相問，卡片之間露

出了三個正方形的空白（圖中陰影部分），已知卡片的短邊長度是\2crn.現要將這三個

正方形的空白用三張圖片填補，則一張圖片的邊長應為cm.

39.同學們，你們玩過積木嗎？現有兩個同樣大小的正方體積木，每個正方體上相對兩個面

上寫的數字之和都等于-2,將這兩個正方體并列放置，看得見的五個數字如圖所示，則

看不見的七個數字之和等于

-22X2013-4.16X(-1)3X|1-2+3-4-5-6+7-8+9-10|

40.計算：--------J----1-----------1------------------=.

(+-----+,?,+----------)X(-

Vl+21+2+31+2+3+…+9，v'

41.方程岫1卜3|=18的解的個數為個.

42.一個等差數列共25項，如果它前10項的和比后5項的和大10,后10項的和比前5項

的和小l（X）,那么，整個等差數列的和是.

43.周長為II且邊長都是正整數的梯形的個數為個.

44.如圖，三條長度相同、兩兩夾角為60°的線段AZ）、8E、C尸交于同一點O.如果△Q4a

△OC。、ZXOE廠的面積之和是且以AZ）、BE、。產為三邊的三角形面積為1.則以

16

AB、CD.E尸為三邊的三角形的面積為.

第7頁共46頁

B

45.從甲地到乙地是上坡路，從乙地到丙地是下坡路，王燕同學自甲地途經乙地到丙地，立

即再沿原路返回甲地，共用3.5小時，已知王燕上坡速度相同，下坡速度也相同，并且走

上坡路所用時間比下坡路所用時間多0.5小時.那么，王燕走上坡路共用了小時.

46.若(2X2-X-1)3=四6+。|/+〃44+。3%3+。4/+。5.1+。6，則41+。3+。5=.

47.如果MW3,|y|Wl,|z|W4,且僅-2y+z|=9,則f)'6=.

48.已知：a=-3y+6焉，b—(-1)100+3白+(-5］，c=(^—4)x(-2J,d=—

(-3)2,則aXAXc+d=.

49.若兩位數除以它的數字和等于7,則這樣的兩位數有個.

50.已知x-2y=l,則/-4)2-x-2y+5=.

51.如圖，已知4、B、C三點在同一個圓上，并且4B是圓。的直徑，若點C到AB的距

離CD=5t則圓。的面積最小是.

DO

52.如圖，在邊長為1的正方形中，分別以四個頂點為圓心，作半徑為1的圓弧，則圖中陰

影部分的面積是.

53.如圖，在梯形A8CO中，BA//CD,AD1AB,AB=7,CD=6m,BC=m2,若以BC為

直徑的圓與AD沒有公共點，則機的取值范圍是.

B

7

6m

A由

第8頁共46頁

54.設/(x)是關于x的多項式，f(x)除以2(x+l),余式是3；2f(x)除以3(.12),

余式是-4,那么，3f(x)除以4(x2-x-2),余式是.

55.已知實數a,b滿足a2+ab+b2=1,則t=a2-ab+b2的取值范圍為.

O

56.如圖，已知AABC中，CDJLAB于點。，BD=2AD,CD=6,cos^ACD=^BE是AC

邊上的高，則40=,BE=.

三.解答題(共4小題)

57.已知正方形ABCD如圖所示，連接其對角線AC,ZBCA的平分線CF交AB于點F,

過點B作BMLCF于點N,交4c于點過點C作CPJLCF,交A。延長線于點P.

(1)求證：BF=DP-,

(2)若正方形48CQ的邊長為4,求△ACP的面積;

(3)求證：CP=BM+2FN.

58.課上，劉老師說：“下面我們要用天平稱出質量相等的A,3兩種粉末狀藥品，藥品不

能直接放在托盤上，…”，這時，劉老師發現上講臺時少帶了一只燒杯，他環顧四位，見

廢紙簍里有一張美術課上丟棄的三角形厚紙板(質地均勻)，于是從容一笑，繼續說到：

“我們可在天平兩個托盤上墊上兩張質量相等的‘限面'，就好比這塊厚紙板”，說著，

他順手將三角形紙板撿起，一量，一點，一畫，一剪，便把它分成了質量相等的兩塊，

然后順利完成了實驗.你知道他是怎樣將三角形紙板分成質量相等的兩塊嗎？他的依據

是什么？

59.三個兩位的完全平方數連在一起寫，得到一個六位的完全平方數，求所有這樣的六位完

全平方數.

60.如圖，A和B是高度同為〃的圓柱形容器，底面半徑分別為T?和凡且rVR.一龍頭單

第9頁共46頁

獨向A注水，用7分鐘可以注滿容器4.現將兩容器在他們高度的一半處用一個細管連

通（連通細管的容積忽略不計），仍用該水龍頭向A注水，問27分鐘時，容器A中水的

高度是多少？（注：若圓柱體底面積半徑為R,高為山體積為匕則V=nR2〃.）

III

AI-------1B

第10頁共46頁

2024年本溪市高級中學中考自招數學復習題

參考答案與試題解析

一.選擇題（共22小題）

4c2AD

1.如圖，在△ABC中，ZC=90°,C7）_L/W于O,在（1）OC?AB=AC?BC；（2）—r=—;

BC2BD

（3）-77+777=（4）AC+BOCD+AB中正確的個數是（）

【解答】解：（1）根據直角三角形斜邊上的高分直角三角形所得的兩個三角形與原三角

形方由以，有：△ACQs/XABC,AAC：AB=DC：BC,

：.DC*AB=AC*BC.所以（1）正確.

AC2AD-ABAD

（2）由射影定理有：AC2=AD^ABBC2=BD?AB,/.—r=---------=—.所以（2）

fBC2BDABBD

正確.

（3）,：AC2=AD*AB,BC?=BD?AB,

又叢ACDs4CBD,：.C0=AD?BD

1111AD+BDAB11”，

:.--+--=------+-------=----------=----------=-------=-所以（3）

AC2BC2ADABBDABADBDABADBDABADBDCD2

正確.

（4）根據三角形兩邊之和大于第三邊，只能得到AC+8OA8,不能得到AC+BO

AB+CD.所以（4）不正確.

故選：B.

2.設〃是正整數，O<^W1,在△A6C中，如果3C=〃+2x,CA=〃十3x,6。邊

上的高那么，這樣的三角形共有（）

A.10個B.11個C.12個D.無窮多個

【解答】解:己知〃是正整數，0<x?l,AB=n+xfBC=〃+2x,CA=n+3x,可知在△

ABC的三個角中，NC最小，

根據余弦定理，得

AB2=B（^+CA2-2/?C?CA?cosC

第11頁共46頁

cosC=(叱+。屋-4解)4-(24C?CA)

=[(n+2x)2+(H+3X)2-(n+x)2J-rl2*(n+2x)*(n+3x)]

=(〃+6x)：[2?(〃+3x)]

在RT4ADC中,

CD=CA*cosC=(n+3.v)e(n+6.r)-i-[2*(/?+3x)]=(〃+6x)4-2

根據勾股定理，得

CA2=AD2+CD2

(〃+3x)2=n2+(〃+6x)2-r4

n=\2x

x=n-r-12

OVxWl

OV〃+12W1

0V〃W12

因〃是正整數，故這樣的三角形最多共有12個.

故選：C.

3.某輪船往返于A、8兩地之間，設船在靜水中的速度不變，那么，當水的流速增大時，

輪船往返一次所用的時間()

A.不變B.增加

C.減少D.增加，減少都有可能

【解答】解：設全程為5,船在靜水中的速度為匕水的流速為V水，往返一次所需時間

為;+當水的流速度增大時，則不妨設水的流速由V水I，變為丫木2,所以，

u+v水v-v/K

時間差為(西京一+—)-(內京一+由京一)

次1"‘次1""水2vV水2

2SV2SV

=晨P■(P"，2)(v

vcv+v^o(v-V>KI)-(K+V水2)(v-v水2)=v水2?-v次J,。，

???V木2>V水1

???當水速增加時，往返一次時間變長.

故選：B.

4.當x=l,y=-l時，ax+by-3=0,那么，當x=-l,y=1時，ax+by-3=()

A.-6B.-5C.-4D.-3

第12頁共46頁

【解答】解：,??當x=Ly=?1時，a?b?3=0,

即4-b=3,

，當x=-1,y=\時，

ax+by-3=-a+b-3=-3-3=-6.

故選：A.

5.已知pq-l=x,其中p,q為質數且均小于1000,x是奇數，那么x的最大值是（）

A.1991B.1992C.1993D.1994

【解答】解：,.,pq-1=x,〃、q為質數，x是奇數，

；?pq為偶數,

，〃與q中必有一個是偶數，不妨設〃=2,夕為質數且qV1000,

?“最大取到997,而x=pq-1的最大值為1993.

故詵：C.

6.P是凸四邊形內的一點，夕與四個頂點連接得到的四條線段的長分別為1,2,3,4.那

么，這個四邊形的面積的最大值為（）

A.10.5B.12C.12.5D.15

【解答】解：圖（1）中，設△EFG的邊產G=a、EG=b,過E作EH上FG于H,

廠EH

sinG=-^-9

：.EH=bsinG,

SAEFG=替FG?EH=^absinG,

要是△EFG的面積最大，當a、〃一?定時，sinG最大，

即sinG=l,即NG=90°.

同理：連接以、PB、PC、PD,

,:S四邊形A8CD=S△附B+SAPBC+S^PCO+S△以D,

要是四邊形ABC。的面積最大，必須△必仄△PAC、△PCD、的面積最大，

由上面證明可知當兩邊一定時，兩邊的夾角是直角時面積最大，

即AC_LB。時面積最大，

有下面三種情況：

（1）當8。=1+2=3,AC=3+4=7時，S=1x3X7=10.5；

第13頁共46頁

1

(2)當80=1+4=5,AC=2+3=5時，5=x5X5=12.5；

(3)當30=1+3=4,AC=2+4=6時，S=1x4X6=12；

???四邊形A4CO的面積的最大值是12.5.

故選：C.

7.我們勸一些較大的數設計出一種簡單的記法：對〃個連續出現的d,記為力.其中〃是

正整數，d是一個一位整數(0WdW9).例如93857462表示99988888777766.如果

2x3y5z+35t2)，=53835373,那么x,y,z的值分別是()

A.4,5,3B.3,6,3C.3,5,4D.5,3,4

【解答】解：一一試驗A,B,C,。四個選項：

4、K=4,y=5,z=3代入：

222233333555+333555522222=555788855777,與結果不符；

B、x=3,y=6,z=3代入，得

222333333555+333555222222=555888555777,與結果相符.

C、x=3ty=5,z=4代入：

222333335555+333355522222=555688855777,與結果不符；

。、工=5,y=3,z=4代入：

222223335555+333355555222=555788900777,與結果不符；

故選：B.

8.如圖，是一座建筑物的平面圖，其中的庭院有兩處供出入的門，過路的人可以在門外觀

看但不能進入庭院，圖中標明了該建筑物的尺寸（單位：米），所有的壁角都是百角，那

么過路人看不到的門內庭院部分的面積是（）

第14頁共46頁

A.250B.300C.400D.325

【解答】解：如圖1：連接8K,并延長到。，連接AW,并延長到E,連接AB,DE,做

CG±DE,CR±AB,

根據圖上所標數據可知:

?.?/18=40,DE=20,BX=KX=IO,

：,KE=DE=2(),

???RG=30,

：.AB：DE=RC：CG,

CR=20,CG=\0,

/.SAC￡D=1X20X10=100,

???矩形E/y。面積為：20X10=200,

如圖2：???NEAB=NEBA=45°,

VAZ?=40,

:?AE=BE=2()&,

???在RtZXAf：產中，EF=20,

.\HE=10+15=20=5,

,:△CDEsWAE、

CDHE

??一,

ABFE

CD5

即—=

4020

ACD=10,

11

???S?COD=3CD?HE=4X10X5=25,

???過路人看不到的門內庭院部分的面積是：200+100+25=325.

故選：D.

第15頁共46頁

JOH.

D

9.如圖，△ABC中，AB>AC,AD,AE分別是其角平分線和中線，過點C作CG_LA￡>于

點凡交AB于點G,連接日則①所〃A&②NBCG=K/ACB-/ABC)；?EF=

乙乙

(4B-AC)；@i(AB-AC)<AE<^CAB+AC).其中正確的是()

BED

A.①②③?B.@@C.②③④D.?@?

【解答】解：：八。平分NBAC,

：.ZGAF=ZCAF,

9：CGIAD,

：.^AFG=Z.AFC=W,

在△A/G和△AR?中

ZGAF=乙CAF

AF=AF

/AFG=乙AFC

/.AAFG^A/\FC(ASA),

:?GF=CF,

???4E為△ABC的中線，

:.BE=CE,

:.EF〃AB,故①正確;

第16頁共46頁

,/AAFG^AAFC,

JNAGC=ZACG,4AGF=ZACF,

???ZAGC=ZB+ZBCG,

:.ZACG=ZB+ZBCG,

工ZBCG=NACB-ZACG=/ACB-(ZB+ZBCG),

；?2NBCG=NACB-NB,

AZBCG=1(NACB-ZB),故②正確：

△AFG@XNFC,

：.AC=AG,

：.BG=AB-AG=AB-AC,

??/、E分別是CG、8c的中點，

:,EF=\BG,

：.EF=^(AB-AC),故③正確；

V^AFG=90°,

/.ZEAF<90°,

VZAFE=ZAFG+ZEFG>90a,

二ZAFE>NEAF,

：.AE>EF,

V￡F=1(AB-AC),

：.-(AB-AC)<AE,立

2

延長AE到M,使AE=EM,連接BM,

第17頁共46頁

???在△ACE和中

(AE=ME

\z-AEC=乙MEB

(CE=BE

:.AACE^AMBE(SAS),

：,AC=MB,

在△/WM中，AM<AB+MB=AB+AC,

\*AE=EM,

：.2AE<AB+AC,

：.AE<^(AB+AC),

乙

即工CAB-AC)<AE<^CAB+AC),故④正確；

故選：A.

10.某油漆專賣店，昨日進了“金魚”、“三葉”、“力王”三種品牌油漆，相同牌子的顏色相

同，不同牌子的顏色不同.已知蘭花白的每桶3千克，百合彩的每桶4千克，風鈴彩的

每桶5千克.為了方便顧客，將三種油漆都分裝成1千克的小桶，結果“金魚牌”油漆

裝了280桶，“三葉牌”油漆裝了255桶，“力王牌”油漆裝了292桶，則“金魚”、”三

葉”、“力王”三種油漆的顏色分別為()

A.風鈴彩、蘭花白、百合彩B.百合彩、蘭花白、風鈴彩

C.蘭花白、風鈴彩、百合彩D.蘭花白、風鈴彩、百合彩

【解答】解：由題意得，“金魚牌”油漆有280依，“三葉牌”油漆255依，“力王牌”油

漆292依，

又蘭花白的每桶3千克，百合彩的每桶4千克，風鈴彩的每桶5千克，

而能被3整除的只有255,即蘭花白對應“三葉牌”，

其余能被5整除的只有280,即風鈴彩對應“金魚牌”，

所以百合彩對應“力王牌”.

故選：4.

11.小明在操場觀看投擲標槍，如圖是他看到的一次標槍飛行圖象，若按標槍飛行先后順序

將下列圖象排序，正確的是()

第18頁共46頁

A.④③?B.④?①⑤②C.③④①⑤②D.③④⑤①②

【解答】解：標槍頭向上，傾斜角最大的是③，進而變小是④，變成水平是⑤，扎地前

是①，最后是②,

即順序為③④⑤①@,

故選：D.

12.已知圖中三十六個小等邊三角形的面積都等于1,則三角形48c的面積為（）

A.21B.22C.23D.24

【解答】解：由圖形結合已知條件可得三個小三角形的面積相等，即三個小三角形全等，

兩個小三角形可拼成一個平行四邊形，且其面積為10個小三角形，

所以一個小三角形的面積為5,

故△4BC的面積為3675=21.

故選：A.

13.甲車在一已知時段內以固定的速度行進（如圖中的虛線所示），在同一距離內，乙車則

以兩倍的速度行進.若乙車的速度與時間以實線表示，則正確描述這種情形的是（）

第19頁共46頁

【解答】解：???兩車均以勻速行駛，

???其圖象是平行于X軸的直線，

???乙車速度是甲車的2倍，

，乙車行駛相同距離所用時間少于甲用時，

故選：B.

14.五個學生正在向前方某人示意一個五位數，站在五個學生的身后看到這個五位數是

A.65432B.34526C.42635D.53624

【解答】解：從身后看到的手勢旋轉180°,排尾變排頭，實際上是從身后看到的手勢關

于直線，的對稱示勢，如圖所示，即為從身前看到的手勢.

所以他們示意的數字是42635.

故選：C.

15.完成一項工作，甲單做需。天，乙單需做〃天，甲、乙、丙合作需。天，則丙單做全部

工作所需的天數是()

abcabc

A.----------------B.----------------

ab-ac-bcab-vac-bc

ab+ac+bcab(c-a-b)

C.----------------

abcc

【解答】解：?.?甲單做需。天，乙單需做〃大，甲、乙、丙合作需c天,

第20頁共46頁

???甲每天完成總工作量的：乙每天完成總工作量的：;，甲、乙、丙合作每天完成總

ab

工作量的：-?

c

???丙單做全部工作所需的天數是：i

1abt-ac-btc.

故選：A.

v—1Irix4-1

16.已如x#-l,0,1,則;----------------;的值可能是（）

|x-l|x|x+l|

A.比3大的數B.比-3小的數

C.±1,±3D.比-3大，并且比3小的數

X-1|%|X+1

【解答】解：當XV7時,--------4--+--------=-1-I-I=-3；

\x-l\X\x+l\

,,x-1Ixlx+l

當-IVxVO時，-——-——-=-1-1+1=-1；

|x-l|X|x+l|

,,x-1Ixlx+l

當OVxVl時，-——-+—+-——-=-1+1+1=1；

\x-l\X|x+l|

,x-1Ixlx+l

當X>1時，----77=1+1+1=3.

|x-l|X|x+l|

故選：C.

17.如圖，梯形/WCO中，A6〃CO,兩條對角線交于點E.己知的面積是m4CDE

的面積是4則梯形ABCO的面積是（)

A.cr+lrB.V2(a+b)C.(口+圾2D.(a+b)2

【解答】解：???AB〃CD,

???AAEBSACED,

.S^AEBA

??=~=()9

S^CEDbDE

BEy/a

，法=帚

,:叢AEB的邊BE上的高和AAOE的邊。￡上的高相司，設此而為h,

.S^AEB==里=生

S&CED^XDEx/iDE4b

*.*S^AFR=at

第21頁共46頁

/.SMDE=4ab，

同理S^BEC=Vab,

，梯形ABCD[filtR^8：S^AEB+SMDE+S^DEC+S^BEC=a+Vab+Z?+VaF=（V?+V^）2.

故選：C.

--------,5

全.

18.如圖，ABA-BC,AB=BC,點、D在BCE以。為直角頂點作等腰直角△人QE,見當。

從B運動到C的過程中，點E的運動軌跡是（）

cDB

A.圓弧B.拋物線C.線段D.雙曲線

【解答】解：如圖所示：

當。點與4點重合時，E點與C點重合，

當。點在BC中點時，

VZADB+ZEDF=90°,

^DAB+^EDF=9Q°,

:./DAB=/EDF,

???在△AO8和△OFE中，

4B=49=90°

乙BAD=乙FDE,

AD=DE

:.XADB9RDFE(/L4S),

；?BD=EF,

'：AB=BC,BD=CD,

:.FC=CD=EF,

:./ECF=/FEC=45°,

當。點與C點重合時，???AB=BC,N8=90",

???NACB=45°,此時E點與另兩個￡點在一條直線上,

第22頁共46頁

故當。從B運動到C的過程中，點E的運動軌跡是線段.

故選：C.

%+x2+x3=

19.已知實數xi,X2,孫m滿足條件?ty3ty4_；2，其中a\<a2<a^<a4,貝Uxi,X2,

X3IX4IX]—U3

+xr+x2=a4

X3>X4的大小關系是()

A.A1<A-2<X3<X4B.X2<X3<X4<A1

C.A3<X2<XI<X4D.X4<X3<A2<XI

①

Q

X1+x+x1

23②

Q2

x+x+x

224①

【解答】解:Q

%3+34+X3

1④

Q4

x4+勺+無2

A?-②得：xi-X4=a\-04VO,則xiVx4,

①-③得：X2-X4=a\-?3<0,則X2〈X4,

①■④得：X3-X4=a\-674<0,則X3〈X4，

②■③得：X2-X\=a2-6f3<0,則X2<XI,

②-④得：A3~XI=42~?4<0,則X3<X\,

③-④得：X3-X2="3-44<0,則X3〈X2,

故Al,XI,X3，X4的大小關系是X3<X2<X\<X4.

故選：C.

20.已知2WMW3,則函數)=(X-1)2的取值范圍是()

A.和9WyW16B.9W〉W16

C.4W)W9D.10W9

【解答】解：???2W|x|E3,

???-3?2,2WxW3,

當x=-3時，y=(x-1)2=(-3-1)2=16,

當x=-2時，y=(x-1)2=(-2-1)2=9,

此時，9WyW16,

第23頁共46頁

當x=2時，y=（x-1）2=（2-1）2=1,

當x=3時，y=（x-1）2=（3-1）2=4,

此時，1W）W4,

綜上所述，函數的取值范圍是和9WyW16.

故選:A.

21.如圖，已知梯形人8c。中，AB//DC,ZA=a,ZC=p,貝l"。：等于（）

A.sina：cospB.sina：sinpC.sinp：sinaD.cosa：sinp

【解答】解：作4E_LBC,BFVBC,則AE=8F,設AE=B尸=a,

???在直角△ADE中，sinO=器=%，

??3薪,

同理，BC=急,

乂???梯形4BCZ）中，AB//DC,

AZ￡>+Za=l80o,

aa

?A八

??一sinD-sina,

.\AD：BC=-^―：.八=sinP：sina.

smasin/?H

故選：C.

A-2-2/7U+I的圖象與端點在（-1,1）和（3,4）的線段只有

一個交點，則〃?的值可能是（）

511

A.-B.C.一D.-

223

【解答】解：方法一：由題意得二次函數對稱軸為工=機，且二次函數過點（0，I）.

①〃7=0,拋物線與線段顯然有兩個交點.

第24頁共46頁

②m>0,對稱軸在右方，則在區間［-1,0］之間兩者必有一個交點，當，〃=1時拋物線還

同時與線段的右端點（3,4）相交，當機>1時拋物線與線段只有一個交點了，故拋物線

與線段只有一個交點，此時求得，〃>1.

③mVO,對稱軸在左方，則在區間［0,3上必有一個交點，當〃『一寸拋物線還同時與線

段的左端點（-1,1）相交，當，"V—2時拋物線與線