C程序設計專題輔導課

算法基礎

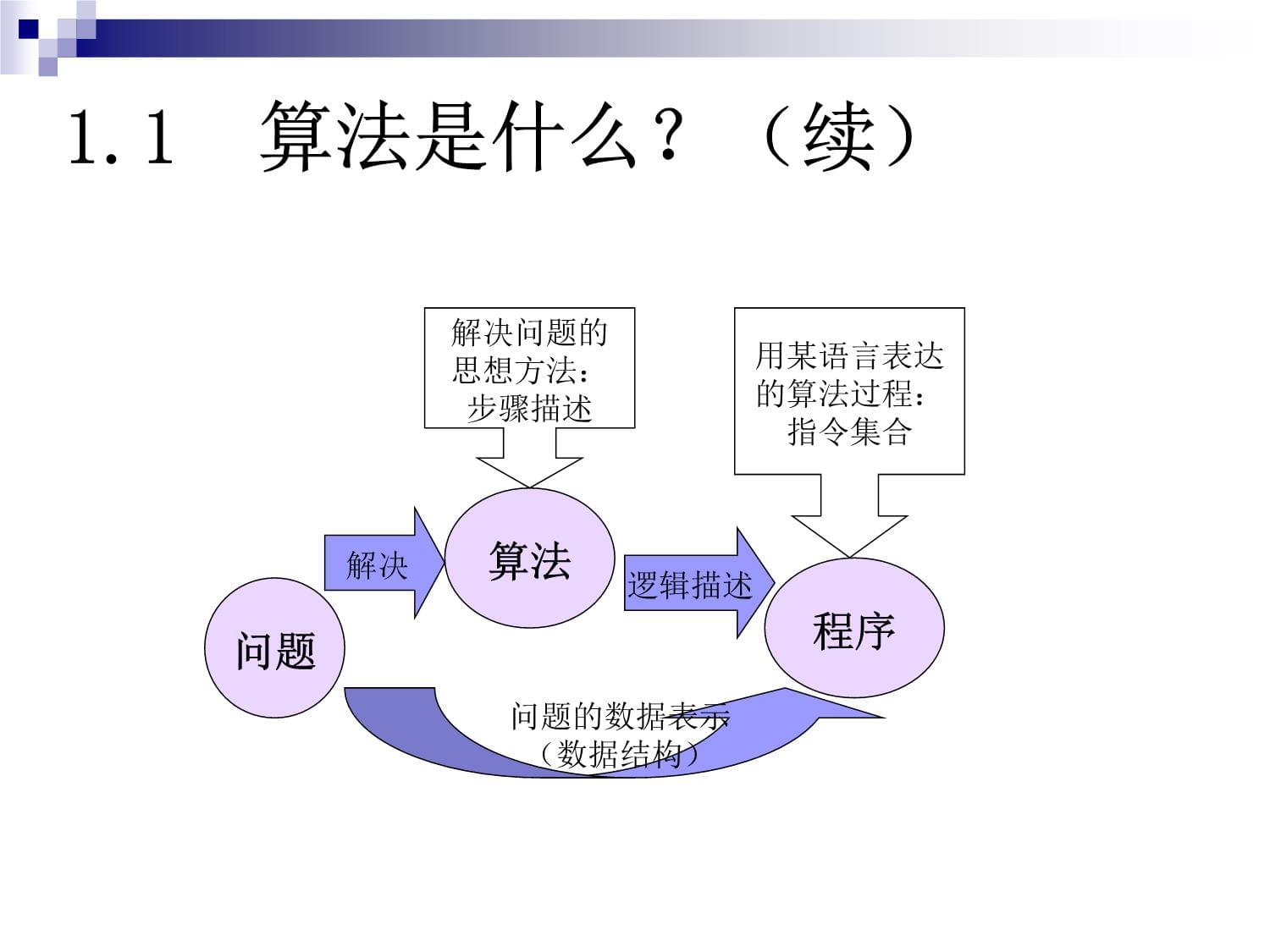
內容提要：算法(algorithm)的概念算法的表達典型算法及其實現—排序查找其它算法一、算法的概念1.1算法是什么？1.2算法的五個要素1.3簡單算法－程序的例子1.1算法是什么？算法：解決特定類型問題的方法和步驟著名的Wirth公式：數據結構+算法=程序1.1算法是什么？（續）算法程序邏輯描述解決問題的思想方法：步驟描述用某語言表達的算法過程：指令集合問題解決問題的數據表示（數據結構）1.2算法的五個要素確定性：對同一個算法，相同的輸入應該得到相同的輸出，不會因為不同的機器和不同時間運行而不同有窮性：算法中的步驟應該是有限的，否則計算機就會永遠無休止地執行程序有效性：算法中的每一個步驟都應該能被有效地執行，并應能得到一個明確的結果（大象裝入冰箱的問題）輸入：有零個或多個輸出：有一個或多個

1.3簡單算法－程序的例子歐幾里德（Euclid）算法：求兩個正整數A和B的最大公約數計算過程舉例：設A=18B=30①A=30B=18②C=A%B=12③A=18B=12④C=A%B=6⑤A=12B=6⑥C=A%B=0⑦最大公約數就是B=6第一步：比較A和B這兩個數：A設置為較大的數，B為較小的數；第二步：A除以B，得到余數C；第三步：如果C等于0，則最大公約數就是B，算法結束；否則將B賦值給A，C賦值給B；第四步：重復進行第二步、第三步。int

Euclid(inta,intb){intc;

if(a<b){c=a;a=b;b=c;}

while(c=a%b){a=b;b=c;}returnb;}二、算法的表達2.1用自然語言描述算法2.2用流程圖描述算法2.3用偽代碼描述算法2.1用自然語言描述算法問題：判斷一個正整數n是否為素數的算法。算法描述一：將n作為被除數，用2到n平方根的各個整數輪流去除，如果都不能整除，則n是素數；否則n不是素數。算法描述二：第一步：輸入n的值,計算n的平方根m；第二步：j=2(用j去除n)；第三步：n被j除，得到余數a；第四步：如果a==0，表示n能被j整除，

顯示信息“n不是素數”，算法結束；

否則進入下一步；第五步：將j加1送回給j；第六步：如果j<=m,則跳到第三步執行；

否則顯示“n是素數”的信息，算法結束。2.2用流程圖描述算法2.3用偽代碼描述算法int

prime(intn){m=n的開方;for(j=2;j<=m;j++){if(n被j整除)

break;}if(j>m)return1;/*是素數*/elsereturn0;

/*不是素數*/}歐幾里德（Euclid）算法：int

Euclid(inta,intb){if(a<b

)交換a和b;c=

a除以b的余數;while(c!=0){a=b;b=c;c=

a除以b的余數;}

returnb;

/*最大公因子*/}三、典型算法及其實現3.1排序算法

3.2查找算法

3.3常用算法舉例

3.1排序算法1、選擇排序2、冒泡排序3、插入排序4、*歸并排序問題：給定n個元素的數組a，對其中的元素從小到大排序，結果仍然在數組a中。排序算法－選擇排序35281設n=5；5個數是：35281(1)15283(2)2583(3)385(4)58排序算法－冒泡排序35281設n=5；5個數是：35281(1)3

2

5

1

8

(2)2

3

1

5

8

(3)2

1358

(4)1

2

358冒泡排序(偽代碼算法)voidBubbleSort(inta[],intn){

for(end=n-1;end>0;end--){

for(i=0;i<end;i++)if(

a[i]>a[i+1]){交換a[i]和a[i+1];}}

}

Entern:5Enter10integers:35281Aftersorted:12358排序算法－插入排序void

InsertionSort(inta[],intN){

intj,P;

int

Tmp;

for(P=1;P<N;P++){

Tmp=a[P];/*下一個元素*/

for(j=P;j>0&&a[j-1]>Tmp;j--) a[j]=a[j-1]; /*前面已排序的部分元素后移，在合適地方的給新元素留出位置*/ a[j]=Tmp;/*新來元素放入合適的位置*/}/*for-P循環結束*/}排序算法－插入排序35281設n=5；5個數是：35281(1)3(2)3

5(3)23

5(4)23

5

8(5)123

5

8

1、合并兩個有序序列：1132426215273812AptrBptrCptrAptrCptrBptrCptr排序算法－歸并排序void

MSort(intA[],int

TmpArray[],intLeft,intRight){

intCenter;

if(Left<Right){/*還有元素需要排序*/ Center=(Left+Right)/2;

MSort(A,TmpArray,Left,Center);

MSort(A,TmpArray,Center+1,Right);

Merge(A,TmpArray,Left,Center+1,Right);}}void

Mergesort(intA[],intN){

int

TmpArray[MAXSIZE];/*臨時工作空間*/

MSort(A,TmpArray,0,N-1);

}2、遞歸歸并排序算法/*Lpos=左半邊起始位置,Rpos=右半邊起始位置*/void

Merge(intA[],int

TmpArray[],int

Lpos,int

Rpos,int

RightEnd){

inti,LeftEnd,NumElements,TmpPos;

LeftEnd=Rpos-1;

TmpPos=Lpos;

NumElements=RightEnd-Lpos+1;

while(Lpos<=LeftEnd&&Rpos<=RightEnd)/*mainloop*/

if(A[Lpos]<=A[Rpos])

TmpArray[TmpPos++]=A[Lpos++];

else

TmpArray[TmpPos++]=A[Rpos++];

while(Lpos<=LeftEnd)/*Copyrestoffirsthalf*/

TmpArray[TmpPos++]=A[Lpos++];

while(Rpos<=RightEnd)/*Copyrestofsecondhalf*/

TmpArray[TmpPos++]=A[Rpos++];

for(i=0;i<NumElements;i++,RightEnd--)

/*CopyTmpArrayback*/

A[RightEnd]=TmpArray[RightEnd];}3、迭代（非遞歸）歸并排序算法A0123…………n4n3n2n1…………………………排序算法－歸并排序設n=6；6個整數是：352871(1)352871(2)3

5

28

17

(3)23

58

17

(4)123

5

78

352817(1)352

871(2)3

5

2

87

1

(3)3

5

2

8

7

1(3’)3

5

2

78

1(2’)23

5

178(1’)123

5

78

迭代算法示例：遞歸算法示例：3.2查找算法1、順序查找2、二分查找3、二分查找推廣－非線性方程的根問題：給定n個元素的數組a，查找某元素x是否在數組a中。如果在，返回該元素在數組中的下標，否則返回-1。順序查找——從列表的第一個數據（或叫做元素）開始，如果給定的數據和表中的數據匹配時，查找過程結束，給出這個數據所在表中的位置（下標）。3.2查找算法－順序查找int

Find(inta[],intn,intx){inti;/*n個元素存放在a[1]-a[n]中*/a[0]=x;/*“哨兵”*/

for(i=n;a[i]!=x;--i);returni;}int

Find(inta[],intn,intx){inti;

/*n個元素存放在a[0]-a[n-1]中*/

for(i=0;a[i]!=x&&i<n;++i);returni;}二分查找——也叫折半查找。比較列表處于一半（中間）位置的數據是否與要查找的數x相同，相同則結束查找，否則判斷是在前半部分還是后半部分（根據列表的排序確定的），然后繼續同樣的查找過程。

查找不成功的條件是查找區間已經<=0。3.2查找算法－二分查找二分查找要求數據已經排序。二分查找比順序查找快得多！3.2二分查找算法一個有點類似的問題－－猜價格游戲：保證在較短時間內猜出一件商品的價格（假設給定價格區間[10,1000]元,且是整數）。條件：當報出一個價格時，系統提示：高了、低了或正確。3.2二分查找算法二分查找算法（自然語言描述）：假設數組A的當前查找區間的下標為[low,high]，查找元素為x；

(1)若high<low，查找失敗，算法結束；否則取區間中間下標：mid=(low+high)/2;(2)若x<A[mid]，x在[low,high]的左半區，則調整新區間邊界：low不變,high=mid-1，轉(1)；(3)若x>A[mid]，x在[low,high]的右半區，則調整新區間邊界：low=mid+1,high不變，轉(1)；(4)若x==A[mid]，則找到，算法結束。int

BiSearch(intx,intA[],intn){/*n個元素存放在A[1]—A[n]*/

int

low,high,mid；low=1;high=n;while(low<=high){mid=(low+high)/2;if(x<A[mid])high=mid-1;/*x在左半區*/elseif(x>A[mid])low=mid+1;/*x在右半區*/elsebreak;/*找到！*/}if(low<=high)returnmid;elsereturn0;}

3.2二分查找程序3.2二分查找推廣－非線性方程求根設有非線性方程：

f(x)=0其中f(x)在[a,b]區間內連續且f(a)f(b)<0。因而f(x)在[a,b]區間內至少有一個實根x0，即：f(x0)=0。寫一個程序求f(x)在[a,b]區間內的一個近似實根。結束條件：|f(x)|<ε

或b-a<ε二分法求非線性方程的根二分法求根（自然語言描述）：假設f(x)在[a,b]內連續，且f(a)f(b)<0，給定誤差ε；

(1)若b-a<ε,返回x0=(a+b)/2作為近似根，算法結束；否則取區間中點m=(a+b)/2;若f(m)=0,返回x0=m,算法結束；(2)若f(a)f(m)>0，在[m,b]內必有根，則調整新區間邊界：b不變,a=m，轉(1)；(3)若f(a)f(m)<0，在[a,m]內必有根，則調整新區間邊界：a不變,b=m，轉(1)；double

BiRoot(doublex,double

a,doubleb,doubleeps){/*求值函數doublef(doublex)需要另外定義*/ doublemid,fm,fa=f(a),fb=f(b);

if(fa==0.)returna;if(fb==0.)returnb;

if(fa*fb>0.){FatalError(“Fail”);return0.;}while(b-a>eps){mid=(b+a)/2;fm=f(mid);if(fm)==0.)returnmid;/*找到一個根*/elseif(fm*fa>0.){a=m;fa=fm;}/*留右半區*/else{b=m;fb=fm;}/*留左半區*/}}

3.2二分法求根3.3常用算法舉例例1：輸入n（2≤n≤5，程序不需要對此范圍進行判斷），再輸入n個整數保存到數組a中，通過循環查找n個數中是否有重復的數，如果有則輸出Yes，否則輸出No。

要求在循環過程中，任何兩個數的比較次數不得超過1次（比如對a[0]與a[1]比較后接下去又對a[1]與a[0]比較是不符合要求的），并且要求一旦找到有數重復則立即結束循環。

－－

08年夏考題

#include<stdio.h> voidmain() {inta[5],i,j,n;

scanf("%d",&n);

for(i=0;i<n;i++)

scanf("%d",&a[i]);

for(i=0;i<=n-2;i++){ for((1);j<=n-1;j++){

if(a[i]==a[j])(2); } if((3))

break; } if((4))

puts("No"); else

puts("Yes");

}j=i+1breakj<=n-1i==n-1或i>=n-1或i>n-23.3常用算法舉例例2：函數f(A,…,x)有三個參數,它們分別是已排序(升序)的數組A、整數n(A的當前元素個數)以及x(要插入到A中的整數)。函數f(…)的功能是把x插入A中，而A仍然保持升序，但n增加了1。例如,A的原來5個元素是(2,4,6,8,10),n=5,x=1,程序運行結束后的輸出是1#2#4#6#8#10#。請完成下面程序。

－－06年考題

#include<stdio.h>voidfintA[],int*n,intx){inti;i=__(1)__;while((i>0)&&(x<A[i-1])){__(2)__; i--;}

A[i]=x;(*n)++;}voidmain(){

inti,A[10]={2,4,6,8,10},n=5,x=1;f(______(3)_______);

for(i=0;i<n;i++)

printf("%d#",A[i]);}*nA[i]=A[i-1];A,&n,x3.3常用算法舉例例3：數組元素循環后移問題一個數組中存有n（1<=n<=100）個整數，在不允許使用另外數組的前提下，將每個數順序向后移m（m>=0）個位置（最后m個數循環移至最前面的m個數）。輸入n、m及n個整數，輸出循環后移m位以后的n個整數。輸入：62123456輸出：561234

數組元素循環后移問題（續）1．問題分析輸入的n個整數可以放在一個一維數組中，循環右移一位的操作重復進行m次即可。這種做法的數據移動次數大約是m(n+1)次。2．要點A）“循環右移一位的操作重復進行m次”，B）m可以處理成小于n的數，以減少工作量。當m>n時，可以用m%n代替m，效果相同。但移動次數大約是(m%n)*(n+1)次。

#include<stdio.h>voidshift(intarray[],intn){

inti,array_end;

array_end=array[n-1];

for(i=n-1;i>0;i--)/*n個元素循環位移1位*/

array[i]=array[i-1];

array[0]=array_end;}voidmain(){intnumber[100],n,m,i;……/*輸入*/m%=n;/*當m大于等于n時轉化成等價的小于n的數*/for(i=0;i<m;i++)

shift(number,n);/*n個元素循環位移1位*/……

/*輸出*/}數組元素循環后移問題（續）思考1：如果修改題目要求，允許使用另外一個大小為m（假設n>m>0）數組，則如何提高程序效率？

012345234501思考2：不改變題目的任何限定(即不允許使用另外數組)，能否設計一種移動次數不超過(n+gc)的方法？[gc是最大公約數]

例：n=6,m=4gc=2趟每趟移動n/gc=3個數0tmp:240voidshift_m(intarray[

],intn,intm){

inti,tmp[M];

/*M是>=m的常數*/

for(i=n-1;i>=n-m;i--)/*復制保留最后m個元素*/

tmp[i-n+m