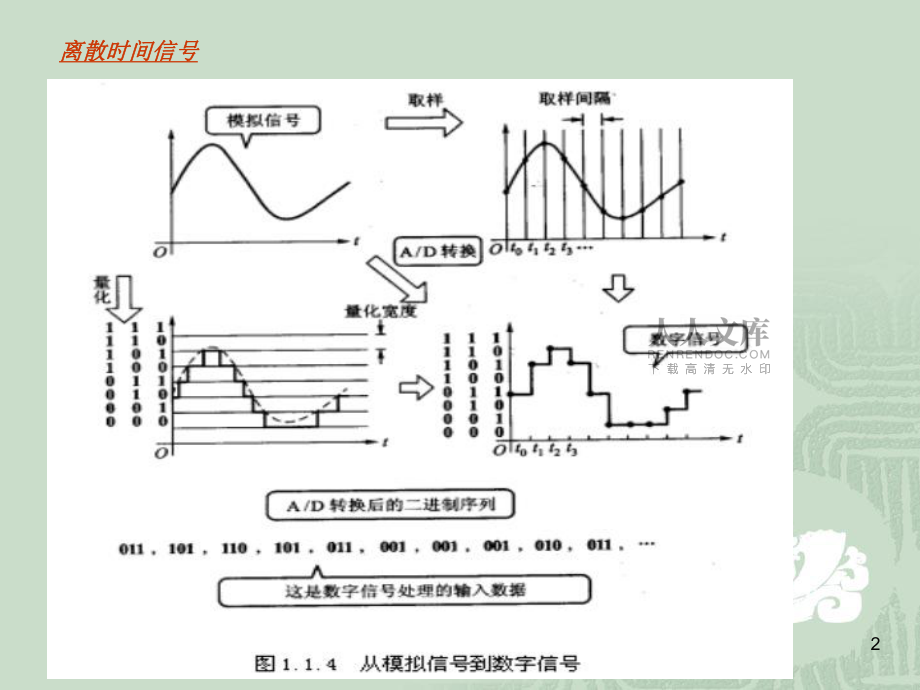
1、1離散時間系統的時域分析離散時間系統的時域分析離散時間信號離散時間信號LTI離散時間系統的差分方程離散時間系統的差分方程抽樣信號與抽樣定理抽樣信號與抽樣定理2離散時間信號離散時間信號3定義：定義：離散時間信號可由連續時間信號離散時間信號可由連續時間信號x(t)x(t)通過抽樣獲得。通過抽樣獲得。設抽樣時間間隔為設抽樣時間間隔為T T，用，用x(nT)x(nT)表示此離散時間信號在表示此離散時間信號在nT nT 點上的值，點上的值，n n為整數。通常情況下直接用為整數。通常情況下直接用x(n)x(n)表示離散序列表示離散序列。4常用典型序列常用典型序列、單位抽樣序列（單位沖激）、單位抽樣序列（單

2、位沖激）(n)(n) (n)在離散序號處理中的作用類似于連續時間信號處理中的沖激函數(t) . (t):是t=0時脈寬趨于0，幅值趨于無限大，面積為1的信號，是極限概念的信號，并不是一個現實的信號; (n):在n=0時取值為1，既簡單又易計算。 0001)(nnn(n)(n)313221n15、單位階躍序列、單位階躍序列u(n)u(n)(n)和u(n)間的關系為令n-m=k代入上式，得0001)(nnnu) 1()()(nunun0)2() 1()()()(mnnnmnnunkknu)()(-3-2-1 n n1u(n)u(n)012363 3、矩形序列、矩形序列RN(n)和(n)、u(n)的

3、關系為為其他值nNnnRN0101)()()()(NnununRN10)()(NmNmnnRR RN N(n)(n)1n nN-1N-2120-17、實指數序列、實指數序列其中a為實數，當|a|1時，序列是發散的。 )()(nuanxna=1.2a=0.98、復指數序列、復指數序列也可以用其實部和虛部表示為或用極坐標表示為其中)()()(0nuenxnjnjenenjnenxnnn0000sincos)sin(cos)(njnnxjeeenxnx0)(arg)()(nnxenxn0)(arg,)(njenenjnxnn612161216121sincos)exp(Real partImagin

4、ary part9、余弦型序列、余弦型序列其中，為幅度，為數字域的頻率，為起始相位。)cos()(0nAnxA010LTI離散時間系統的差分方程離散時間系統的差分方程111、從微分方程到差分方程、從微分方程到差分方程TTnynTyttyttydttdyatftaydttdyt) 1()()()(lim)(0)()()(0tyy(nT)y(n-1)Ty(t)y122、實際問題列寫差分方程、實際問題列寫差分方程例：銀行存款，在例：銀行存款，在t=kT時存入為時存入為f(k)，T為固定時間間隔，這里為個月。為固定時間間隔，這里為個月。銀行的月息為銀行的月息為，每月的利息不取出，使用差分方程寫出第，每

5、月的利息不取出，使用差分方程寫出第k月初的本利月初的本利y(k)。解：設第解：設第k月的本利為月的本利為y(k)，原有存款為，原有存款為y(0)=0)() 1()1 ()(:)2() 1 () 1 ()2(:2) 1 ()0()0() 1 (:1kfkykykfyyyfyyy個月第個月第個月第13例：有一個電阻的梯形網絡，每一串臂電阻值為，每一并臂的電阻值為例：有一個電阻的梯形網絡，每一串臂電阻值為，每一并臂的電阻值為 a，a為某一正實數為某一正實數U(0)=E,U(N)=0 求任一節點的電壓求任一節點的電壓U(k)=?+-EU(0)RRRRRaRaRaRU(k)U(N)14解：取出此電路的一

6、個型結構0)()0(0)2() 1(12)() 1()() 1() 1()2(NUEUkUkUaakUaRkURkUkURkUkUiiicbaRRaRU(k)U(k)U(k)iaibic153、討論、討論）差分方程的自變量可以是時間）差分方程的自變量可以是時間t，也可以是其它的離散變量；，也可以是其它的離散變量；）差分方程的一般形式）差分方程的一般形式）差分方程各項序值如果同時加減同一個數，差分方程描述的輸入輸出關）差分方程各項序值如果同時加減同一個數，差分方程描述的輸入輸出關系不變系不變）方程若想得到確定的唯一解，必須給出初始條件，這與連續系統是一樣）方程若想得到確定的唯一解，必須給出初始條

7、件，這與連續系統是一樣的的MkkNkkknxbknya00)()(16用抽樣序列表示任意序列用抽樣序列表示任意序列離散系統離散系統(n)h(n)x(n)y(n)=x(n)*h(n)連續時間系統連續時間系統任意信號由沖激函數的迭加積分公式表示任意信號由沖激函數的迭加積分公式表示dtxtx)()()(17離散時間系統：離散時間系統：用抽樣序列表示任意序列用抽樣序列表示任意序列不同：不同：（）連續系統中是積分，離散系統中是累加；（）連續系統中是積分，離散系統中是累加；（）連續時間系統中（）連續時間系統中(t-)是單位沖激函數，是單位沖激函數， 離散系統中離散系統中(n-k)是單位抽樣函數，幅度為是單

8、位抽樣函數，幅度為dtxtxknkxnxk)()()()()()(182 15 . 125 . 0nnnnx675. 04nn19抽樣信號與抽樣定理抽樣信號與抽樣定理1、問題提出、問題提出連續時間信號的離散過程要解決的問題：連續時間信號的離散過程要解決的問題：（1）f(t) fs(nT)(不是數字信號不是數字信號)，模擬信號的離散化；，模擬信號的離散化；（2）F(j)與與 Fs(j)的關系離散信號的關系離散信號fs(nT)是否包含是否包含f(t)的所有信息；的所有信息；（3）在什么條件下，）在什么條件下， f(t)可以從離散信號可以從離散信號fs(nT)中完全恢復出來。中完全恢復出來。、抽樣過程、抽樣過