1、 靜定結構的受力分析，主要是利用平衡方程計算支座反力和桿件內力。靜定結構的受力分析，主要是利用平衡方程計算支座反力和桿件內力。作出結構的內力圖。作出結構的內力圖。 隔離體分析是受力分析的基礎。先從結構中截取隔離體，將未知的反力隔離體分析是受力分析的基礎。先從結構中截取隔離體，將未知的反力和內力暴露出來，使其成為隔離體上的外力，而后應用平衡方程計算約束反和內力暴露出來，使其成為隔離體上的外力，而后應用平衡方程計算約束反力和內力。力和內力。1、隔離體的形式、約束力及獨立平衡方程、隔離體的形式、約束力及獨立平衡方程3-7 隔離體方法及其截取順序的優選隔離體方法及其截取順序的優選隔離體的形式：結點（鉸

2、結點、剛結點、組合結點），桿件，某部分。隔離體的形式：結點（鉸結點、剛結點、組合結點），桿件，某部分。 隔離體的形式隔離體的形式 約束力的類型約束力的類型選取隔離體時，在截斷約束處暴露出來的約束力成為隔離體的外力。選取隔離體時，在截斷約束處暴露出來的約束力成為隔離體的外力。截斷鏈桿有一個約束力（截面上的軸力）。截斷鏈桿有一個約束力（截面上的軸力）。 截斷梁式桿（或截斷簡單剛結）一般有三個約束力（截面上的軸力、截斷梁式桿（或截斷簡單剛結）一般有三個約束力（截面上的軸力、剪力和彎矩）。剪力和彎矩）。 截斷可動餃支座、固定餃支座、固定支座時分別加一個、二個、三個支截斷可動餃支座、固定餃支座、固定支座

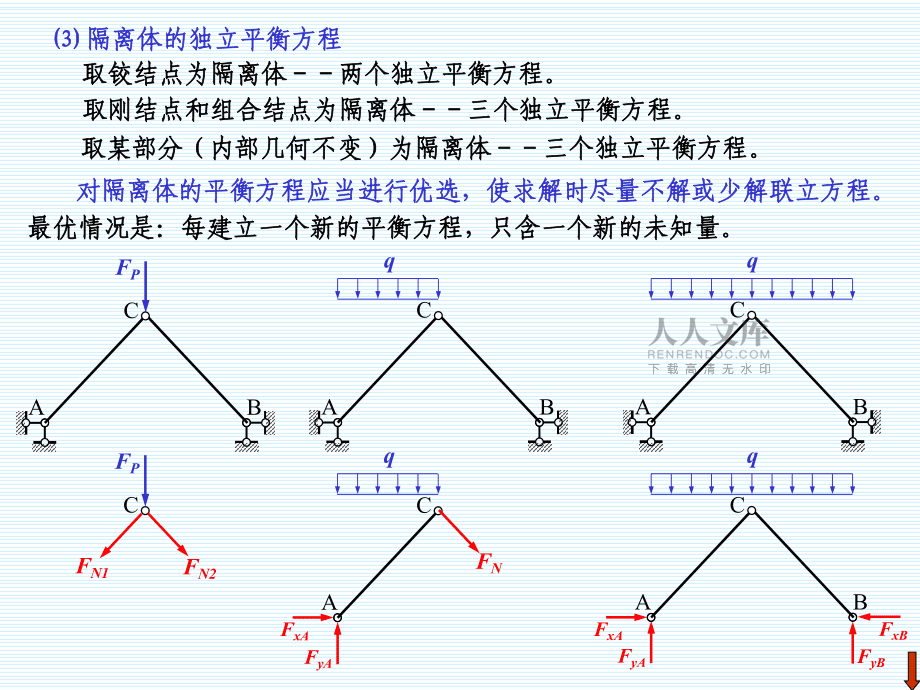
3、時分別加一個、二個、三個支座反力。座反力。截斷簡單鉸結一般有兩個約束力。截斷簡單鉸結一般有兩個約束力。FPC 隔離體的獨立平衡方程隔離體的獨立平衡方程取鉸結點為隔離體兩個獨立平衡方程。取鉸結點為隔離體兩個獨立平衡方程。取剛結點和組合結點為隔離體三個獨立平衡方程。取剛結點和組合結點為隔離體三個獨立平衡方程。取某部分（內部幾何不變）為隔離體三個獨立平衡方程。取某部分（內部幾何不變）為隔離體三個獨立平衡方程。對隔離體的平衡方程應當進行優選，使求解時盡量不解或少解聯立方程。對隔離體的平衡方程應當進行優選，使求解時盡量不解或少解聯立方程。最優情況是：每建立一個新的平衡方程，只含一個新的未知量。最優情況是

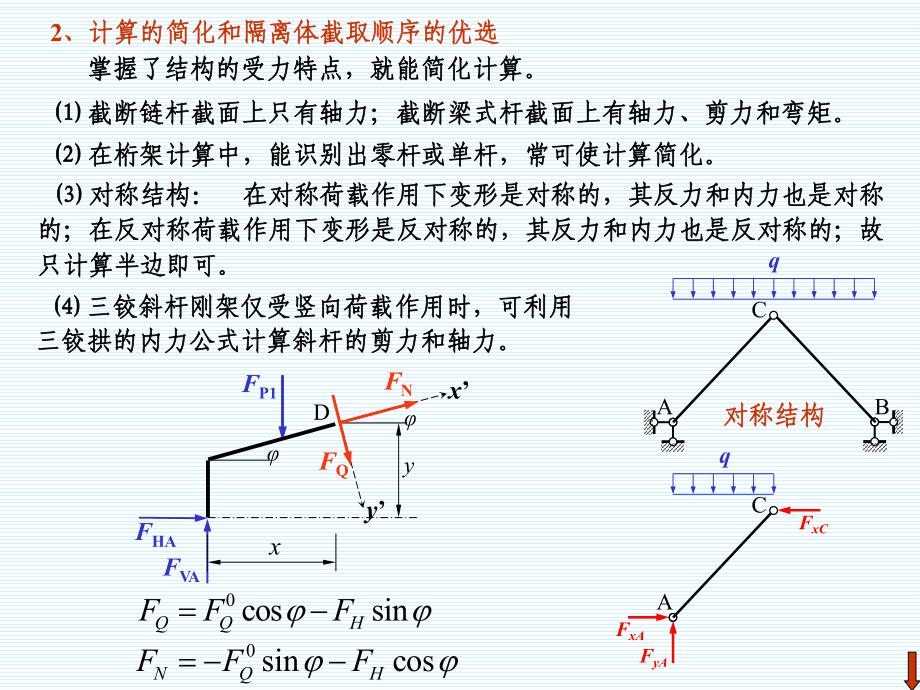
4、：每建立一個新的平衡方程，只含一個新的未知量。FPABCABCABCq FxAFyAFyBFxBABCq q ACq FxAFyAFNFN1FN22、計算的簡化和隔離體截取順序的優選、計算的簡化和隔離體截取順序的優選掌握了結構的受力特點，就能簡化計算。掌握了結構的受力特點，就能簡化計算。 截斷鏈桿截面上只有軸力；截斷梁式桿截面上有軸力、剪力和彎矩。截斷鏈桿截面上只有軸力；截斷梁式桿截面上有軸力、剪力和彎矩。 對稱結構：對稱結構： 在對稱荷載作用下變形是對稱的，其反力和內力也是對稱在對稱荷載作用下變形是對稱的，其反力和內力也是對稱的；在反對稱荷載作用下變形是反對稱的，其反力和內力也是反對稱的；故

5、的；在反對稱荷載作用下變形是反對稱的，其反力和內力也是反對稱的；故只計算半邊即可。只計算半邊即可。 在桁架計算中，能識別出零桿或單桿，常可使計算簡化。在桁架計算中，能識別出零桿或單桿，常可使計算簡化。q FxAFyAFxCACq ABC對稱結構對稱結構 三鉸斜桿剛架僅受豎向荷載作用時，可利用三鉸斜桿剛架僅受豎向荷載作用時，可利用三鉸拱的內力公式計算斜桿的剪力和軸力。三鉸拱的內力公式計算斜桿的剪力和軸力。0cossinQQHFFF0sincosNQHFFF FP1DyxFHAFVAFQFNyxBCFAEGD 基附型結構：基附型結構：多跨靜定梁區分為多跨靜定梁區分為基本部分和附屬部分基本部分和附屬

6、部分。多跨或多層靜定。多跨或多層靜定剛架、多跨靜定桁架也可區分為剛架、多跨靜定桁架也可區分為基本部分和附屬部分基本部分和附屬部分。基附型結構應基附型結構應先計算附屬部分，然后計算基本部分。先計算附屬部分，然后計算基本部分。FP1FP2BCFAEFP1GDFP2FyEFxEFyAFyDFyGFxG3-8 剛體體系的虛功原理剛體體系的虛功原理計算靜定結構內力的另一個普遍方法計算靜定結構內力的另一個普遍方法 虛功原理虛功原理，它等價于平衡方程。，它等價于平衡方程。實功和虛功：實功和虛功： 實功實功 力力 在在由該力引起的位移由該力引起的位移 上所作上所作的功稱為實功。即的功稱為實功。即1PF1 右圖

7、中，外力是從零開始線性增大至右圖中，外力是從零開始線性增大至 ，位移也從零線性增大至位移也從零線性增大至 。也稱為靜力實功。也稱為靜力實功。 1PF1FP11111112PWF 虛功虛功 力力FP1 在由在由非該力引起的位移非該力引起的位移上所作上所作的功叫作虛功。的功叫作虛功。 右圖簡支梁，先加上右圖簡支梁，先加上 ，則兩截面，則兩截面1、2 之位移分別為之位移分別為 、 。1PF12FP11212然后加然后加 ，則，則1、2 截面產生新的位移截面產生新的位移 和和 。122PF實功：實功：虛功虛功：112211,22PPFF11PF“虛虛”強調作功的力與位移無關強調作功的力與位移無關。FP

8、212 表述：表述：設體系上作用任意的平衡力系，又設體系發生符合約束條件的無設體系上作用任意的平衡力系，又設體系發生符合約束條件的無限小剛體體系位移，則主動力在位移上所作的虛功總和恒等于零。限小剛體體系位移，則主動力在位移上所作的虛功總和恒等于零。兩種應用兩種應用: :虛設位移虛設位移 虛位移原理求靜定結構的反力和內力。虛位移原理求靜定結構的反力和內力。虛設力系虛設力系 虛力原理求剛體體系的位移。虛力原理求剛體體系的位移。0XXPPFF PPX10XPpFF XPbFFa1、虛功原理、虛功原理第一種應用：第一種應用：虛設位移，求未知力。虛設位移，求未知力。解：解：扛桿是一個可變體系，可繞扛桿是

9、一個可變體系，可繞 C 點自由點自由轉動，如圖轉動，如圖(b)示。把這個剛體位移取作示。把這個剛體位移取作虛虛位移，可得出虛功方程為：位移，可得出虛功方程為： FXXPFPACB ab(a)例：例：圖圖(a)示扛桿，其中示扛桿，其中B端作用巳知荷載端作用巳知荷載FP ，求扛桿平衡時在，求扛桿平衡時在A端需加的未知力。端需加的未知力。XP 設設 表示位移表示位移 和和 之間的之間的比例系數：比例系數： XPPba ACB(b)ACB(c)通常取通常取 (數值為1)1X單位位移法單位位移法 這里實際用的是剛體虛位移原理，實質上是這里實際用的是剛體虛位移原理，實質上是實際受力狀態的平衡實際受力狀態的

10、平衡方程方程，即，即0CM幾點說明：幾點說明： 求解時求解時關鍵關鍵一步是找出一步是找出虛位移狀態的位移關系虛位移狀態的位移關系。 虛位移與實際力狀態無關，故可虛設。虛位移與實際力狀態無關，故可虛設。用虛功原理求解問題的方法稱為用虛功原理求解問題的方法稱為虛功法虛功法。小結：小結： 求解問題直接，不涉及約束力。求解問題直接，不涉及約束力。 虛功原理（這里用虛位移原理）的虛功原理（這里用虛位移原理）的特點是特點是用幾何方法解決平衡問題。用幾何方法解決平衡問題。bc3cABCDEFaXPdxy解：解： 建立虛功方程建立虛功方程0XXPPFF 幾何關系幾何關系2cos ,sinbaca有虛位移有虛位

11、移 d 時，時，b 和和 c 的變化的變化dadbsin2dadccos由于由于dadbXsin2dadcPcos33cbcbctgXP43223233022XXPXbFFc 34XPbFFc例例3-15：求機構平衡時在求機構平衡時在B點需加的力點需加的力 FX = ? 以以 d 作為位移參數作為位移參數 解方程求解方程求FX FX FX FP FP 2、應用虛功原理求靜定結構的約束力、應用虛功原理求靜定結構的約束力單位位移法單位位移法10XPPFF 例：例：求圖求圖 (a) 示簡支梁示簡支梁 A 端的支座反力。端的支座反力。構造相應的虛位移狀態如圖構造相應的虛位移狀態如圖(b)示。示。1XPFP abACB(a)解：解：去掉去掉 A 端約束并代以反力端約束并代以反力 FX 力系在虛位移上所作的虛功總和力系在虛位移上所作的虛功總和恒等于零。得出虛功方程為恒等于零。得出虛功方程為 FXACB(b)XPPPbFFFa FP FX 單位位移法的一般