1、第三章 線性回歸分析§3.1 一元線性回歸模型一、回歸分析變量之間的關系，大體分為兩類：一類是函數關系；另一類是統計相關關系，或稱隨機關系。具有相關關系的變量間雖然不具有確定的函數關系，但可以根據大量的統計數據，找出變量之間在數量變化上的統計規律，這種統計規律稱為回歸關系。用以近似地描述具有相關關系的變量間的函數關系稱為回歸函數。有關回歸關系的計算方法和理論稱為回歸分析技術。回歸分析的主要內容是：1. 根據樣本觀察值對模型參數進行估計,求得回歸方程;2. 對回歸方程、參數估計值進行顯著性檢驗;3. 利用回歸方程進行預測與控制。二、總體回歸方程1、例子假設一個地區的人口總體由60戶組成

2、。我們要研究每月家庭消費支出Y與每月可支配家庭收入X的關系。也就是說知道了家庭的每月收入，要預測每月消費支出的（總體）平均水平。為此，將這60戶家庭劃分為組內收入差不多的10組，以分析每一收入組的家庭消費支出。表2.1給出了假定的數據.表1.1 X,每月家庭收入(元) XY800100012001400160018002000220024002600每月家庭消費支出550600650700750-650700740800850880-790840900940980-8009309501030108011301150102010701100116011801250-110011501200130

3、013501400-12001360140014401450-1350137014001520157016001620137014501550165017501890-1500152017501780180018501910共計325046204450707067807500685010430966012110表2.1表明:對應于每月800元收入的5戶家庭的每月消費支出為550到750元不等.類似地,給定X=2400元,6戶家庭的每月支出在1370元和1890元之間.即表2.1的每個縱列給出對應于給定收入水平X的消費支出Y的分布.;也就是說,它給出了以X的給定值為條件的條件分布.表2.1的數據

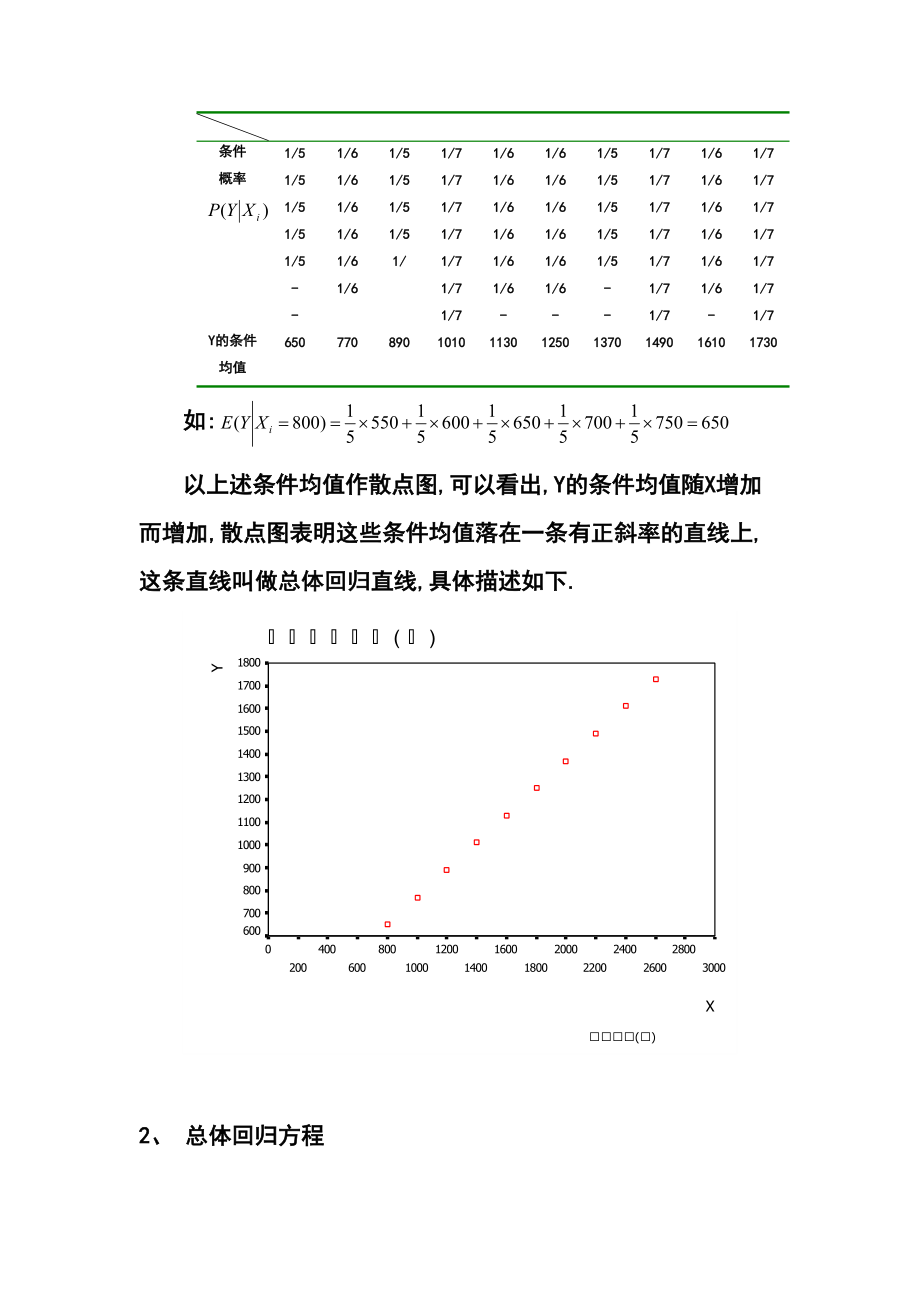
4、代表一個總體.我們可計算出給定X的Y的條件概率.計算如下表2.2 表2.2 與表2.1的數據相對應的條件概率 X800100012001400160018002000220024002600條件概率1/51/51/51/51/5-1/61/61/61/61/61/6 1/51/51/51/51/1/71/71/71/71/71/71/71/61/61/61/61/61/6- 1/61/61/61/61/61/6-1/51/51/51/51/5-1/71/71/71/71/71/71/71/61/61/61/61/61/6-1/71/71/71/71/71/71/7Y的條件均值650770890

5、1010113012501370149016101730如:以上述條件均值作散點圖,可以看出,Y的條件均值隨X增加而增加,散點圖表明這些條件均值落在一條有正斜率的直線上,這條直線叫做總體回歸直線,具體描述如下.2、 總體回歸方程描述兩個變量X與Y之間的線性關系可用下列數學式子表示。 （）（）式中一部分是由于X的變化引起Y線性變化的部分，即；另一部分是由其它一切隨機因素引起的，記為。（2.1.1）式確切地表達了變量X與Y之間的密切程度，但密切的程度沒有達到由X唯一確定Y的地步。（）式稱為Y對X的一元線性回歸理論模型，Y稱為被解釋變量（因變量），X稱為解釋變量（自變量），式中是未知參數，稱為回歸參

6、數，表示隨機因素的影響，是一隨機變量。一般假定和，在此假定下有，或，稱為一元線性總體回歸方程，它是解釋變量取給定值時因變量的條件均值或條件期望值的軌跡.三、樣本回歸方程取一個容量為N的樣本，代入（）式有， （）（）稱為一元線性回歸模型.基本假定:1. 零均值假定 () 由于存在隨機擾動因素, 在期望值附近上下波動,如果回歸方程假定正確, 相對于的正偏差和負偏差都會發生,隨機擾動項可正可負,發生的概率大致相同,零均值假定表明平均來看,這些隨機擾動項有相互抵消的趨勢.2. 同方差假定 ()這個假定表明, 對每個, 隨機擾動項的方差等于一個常數, 即解釋變量取不同值時, 相對各自均值(零均值)的分散

7、程度是相同的, 因變量具有與相同的方差.因此，該假定同時表明因變量可能取值的分散程度是相同的。3無自相關假定 （） 假定表明產生干擾的因素是完全隨機的，此次干擾與彼次干擾互不相關，因此變量的序列值之間也互不相關。4解釋變量與擾動項互不相關的假定 （） 這個假定表明與互不相關，即隨機擾動項和解釋變量是各自獨立地對因變量產生影響的。事實上，在回歸分析中，在重復抽樣（觀測）中固定取值，是確定性變量，故與不相關的假定一般總是滿足。5解釋變量的各觀測值不能近似相同（解釋變量之間不存在多重共線性）這個假定表明與常變量之間不存在某種線性關系。在多元條件下，這個假定要求解釋變量之間不能存在線性相關。6隨機誤差

8、項服從正態分布 此假定是為方便于模型參數的假設檢驗。四、模型參數的估計 在上述假定下， i=1，2，N ()或, i=1，2，N () 對于N組樣本觀測值,對進行估計，用分別表示的估計值，則有 （）（）稱為Y關于X的一元線性樣本回歸方程。如何求出的估計值，最常用的方法是普通最小二乘法（OLS）（Ordinary Least Squares). 設有N組觀測值, 作散點圖. Y 。 。 。 。 。 。 X設估計直線為 （）將代入（） ()由（2.11）中所求的值稱為理論估計值，則實際觀測值與理論估計的誤差為: （）根據最小二乘法的原理，欲使（）式最適合于實際數據（所求回歸直線是在一切直線中最適合

9、實際數據的直線）必須使這些誤差的平方和最小。即必須使 （）為最小（因正誤差與負誤差都是誤差，因此要用平方和消去符號）。根據微積分求極值的原理，欲使（）式最小，則必要條件為：即亦即 （）解得:因此可確定回歸方程 （）若記_ X的樣本方差 _ X與Y的樣本協方差 _ Y的樣本方差則可證:五、一元線性回歸模型的統計檢驗根據變量和的樣本觀測值，應用最小二乘法求得的樣本回歸方程，作為總體回歸方程的近似。這種近似是否恰當，必須進行統計檢驗。統計檢驗包括：擬合優度檢驗、相關系數檢驗、參數顯著性檢驗以及回歸總體線性的顯著性檢驗。（一）、 擬合優度檢驗（檢驗） 0 擬合優度檢驗是指對樣本回歸直線與樣本觀測值之間

10、擬合程度的檢驗，度量回歸擬合程度的指標是判定系數。（1） 總離差平方和的分解設由樣本觀測值得回歸直線 由上圖可看出，Y的第個觀測值與樣本均值的總離差可以分解兩部分，即為樣本回歸直線理論擬合值與觀測值的平均值之差，是由回歸直線解釋的部分.為實際觀測值與回歸擬合值之差，是回歸直線不能解釋的部分。離差大小反映了變量與平均數之間的波動大小，而全部數據的總離差可由這些離差平方和表示，可以證明：記-總離差平方和(Total Sum of Squares)-殘差平方和(Residual Sum of Squares)-回歸平方和(Explained Sum of Squares)故 方差分析表方差來源方差平

11、方和自由度均方差F統計量回歸平方和1殘差平方和總離差平方和（二）、判定系數在總離差平方和中，如果回歸平方和所占比例越大，殘差平方和所占比例就越小，表明回歸直線與樣本點擬合得越好。定義判定系數為: (),若,說明全部樣本觀測值均在估計回歸直線上，觀測與回歸值完全擬合，若，說明完全不擬合，,線性模型完全不能解釋變動，越接近1，擬合程度越好，反之越差。（三）、相關檢驗（r檢驗）變量之間通常是相關的，問題是相關程度如何，如果在相關程度過低的變量間建立線性模型，就沒有很大的意義。兩個變量和之間真實的線性相關程度是由總體相關系數表示:由于總體未知，無法計算，我們可利用樣本值給出一個估計.定義樣本相關系數

12、()是的一個無偏估計量.由()式和(2.1.17)式知:故樣本相關系數與判定系數在計算上是一致的。但兩者的概念不同，判定系數是對變量與作方差分析得出的，用來衡量擬合優度；而相關系數是對與作相關分析得出的，用以判定與的線性相關程度。線性相關檢驗的具體作法如下：1） 建立假設: 2） 根據計算樣本相關系數3） 根據樣本容量N和顯著性水平查相關系數表得臨界值（表中N-2為自由度）4） 判斷：若，則拒絕，認為與有顯著的線性相關關系； 若,則接收，認為與的線性相關關系不顯著。或用F統計量進行線性相關檢驗1） 建立假設2） 選取統計量在成立的條件下, 3） 對于給定的檢驗水平，查表得臨界值，4） 根據樣本

13、觀測值計算出統計量值；5） 下結論：若，則否定。認為與之間存在線性相關關系； 若，則接收，認為與之間線性關系不顯著。事實上這兩種檢驗方法是一致的。因故，的值較大等價于較大。（四）回歸參數的檢驗1. 最小二乘估計的性質在第二節中求得的模型總體參數的估計量在基本假定下，具有下列性質：(1) 線性性和為線性組合。而，令則，即是的線性組合。其中,故 也是的線性組合。因為是隨機變量,故和也是隨機變量.(2) 無偏性無偏性是指估計量和的期望等于總體回歸參數的和的期望。因為而故，由基本假定，所以因為由基本假定,知 最小方差性證明:和的方差為:假設是關于的線性無偏估計量，而故由的無偏性知比較上式兩邊得由的表達

14、式和可證明因此因為,故,當且僅當等式成立. 是有效估計.同理可證明也是有效估計.2、和的分布定理：在以下模型中其中,記分別是的最小二乘估計量，則（1），即（2），即和的標準差分別為，2、隨機擾動項方差的估計由于總體方差未知，因此和的方差實際上無法計算，又由于隨機項不可觀測，我們只能從的估計殘差出發，對總體方差進行估計。可以證明總體方差的無偏估計為，這樣和的樣本方差和樣本標準差分別為：的樣本方差：的樣本方差：的樣本標準差：的樣本標準差：4、關于的檢驗（1） 建立假設：（2） 選取統計量, 其中在成立的條件下, （3） 在給定的顯著性水平,查表得臨界值（4） 根據樣本觀測值計算統計量的值（5） 若

15、，則接收,若，則拒絕，接收.5、 關于的檢驗(1)建立假設：(2)選取統計量,其中在成立的條件下, (3)在給定的顯著性水平,查表得臨界值(4)根據樣本觀測值計算統計量的值(5)若，則接收,若，則拒絕，接收.六、預測預測是回歸分析應用的重要方面.預測可分為點預測和區間預測兩類.點預測是指當時,利用樣本回歸方程,求出相應的樣本擬合值,以此作為因變量個別值和均值的估計.由于抽樣波動的影響,以及隨機擾動項的零均值假設不完全與實際相符.點預測值與因變量個別值及其均值都存在一定的誤差.以一定的概率把握誤差的范圍,從而確定和的波動范圍,此為區間預測.（一）、點預測總體回歸方程的隨機設定形式為: ()樣本回

16、歸方程為: ()當時,Y的個別值為 ()其總體均值 ()樣本回歸方程在時的擬合值為: ()對()式兩邊求期望得: ()由()說明,在時,由樣本回歸方程計算的 是總體均值的無偏估計.因此可以用 作為和的預測值.（二）、區間預測總體均值的預測區間(1) 令,則由模型基本假定服從正態分布.(2) 的期望和方差 () = =可以證明 (2.1.24的方差為= ()(3) 從而有 ()將標準化 ()用代替,由樣本理論分布及的定義,有 ()從而可得的預測區間為:()其中為顯著性水平.2.總體個別值的預測區間(1)定義殘差 ()則由模型基本假定服從正態分布.(2)的期望和方差 ()因與相互獨立,故 ()(3

17、) 從而有 ()將標準化 ()用代替,由樣本分布理論及的定義,有 ()從而可得的預測區間為:()其中為顯著性水平.§2.2 多元線性回歸分析在許多實際問題中影響因變量Y的自變量往往不止一個，比如有k個。討論一個變量對兩個及兩個以上變量的統計依存關系，就是多元回歸模型，如果變量之間是線性關系，則稱為多元線性回歸模型。一、多元線性回歸模型（一）、多元線性總體回歸方程假定因變量Y與K個自變量具有線性相關關系， （）對應于解釋變量的每一組觀察值，因變量的值是隨機的，其可能取值的集合形成一個總體，記為。稱()式及因變量Y的總體條件期望函數 ()為K元線性總體回歸方程。（二）、多元線性樣本回歸方

18、程多元線性總體回歸方程是未知的，只能通過抽取樣本觀察值對之進行估計。對應于()式的總體回歸結構, 多元線性樣本回歸方程的形式為, ()或者,()其中, 是總體均值的估計值, 是總體偏回歸系數的估計,殘差是隨機項的估計。（三）、模型的矩陣表示設有N組觀察值，代入()式,得N個隨機方程令則多元線性總體回歸方程的矩陣形式為：或 （）式中，N維因變量觀察值向量解釋變量觀察值矩陣N維隨機項向量維總體回歸參數向量類似地，多元線性樣本回歸模型可用矩陣表示如下： （）或者 ()簡寫為 () 或者 ()其中, N維因變量回歸擬合值向量維總體回歸參數估計值向量N維殘差向量一、 模型的基本假定1.零均值假定 （）即

19、2.同方差和無自相關假定, () （） 即隨機項的方差協方差矩陣為： () 其中E為N階單位矩陣。 3解釋變量X與隨機項互不相關的假定 （）即 或者 （） 4解釋變量觀察值矩陣滿秩的假定 （）如果該假定成立，X至少有k+1階子式不為零，表明解釋變量之間不存在線性相關關系，此時矩陣也是滿秩的。 所以行列式存在。 在這些假定下，多元線性回歸模型常寫成： （）或進一步假定為： （）二、參數的最小二乘估計及其性質（一）、參數的最小二乘估計類似于一元線性回歸，采用最小二乘估計法，設樣本回歸方程如()式,殘差要求的估計使殘差平方和 ()達到最少。若令 (）由極值原理得正規方程組： ()整理得關于的線性方程

20、組： （）解上述方程組得的最小二乘估計。()也可寫成 ()或者 ()在樣本回歸方程的矩陣形式兩邊同時左乘以觀察值矩陣X的轉置得 ()由極值條件()式,正規方程組用矩陣形式表示為： （）又由X滿秩的假定(可逆)），則參數的最小二乘估計向量為 （）（二）、最小二乘估計的性質擬合值向量用矩陣表示為 ()其中稱為“帽子矩陣”。 殘差向量用矩陣表示為:。殘差平方和，記為，即最小二乘估計有下列幾個性質：1. 線性性是的線性函數.2. 無偏性 即證明: 由模型的基本假定得 ()3. 最小方差性 證明：（1）求 的方差-協方差矩陣 = = = = 該矩陣主對角上給出了各個參數估計值的方差，而在其余部分給出了不

21、同的參數估計值和的協方差。由及基本假定有=()若記中的元素為,則 （） () （）僅當時與不相關。(2) 若是的線性無偏估計,設,令則可以表示為 ()從而 ()因是的無偏估計,又由基本假定知從而 ()于是 ()的方差-協方差矩陣為=+= +=+=+ ()在此,用到,也有，及. ()而為半一正定矩陣，其主對角線上的元素大于等于零，設其主對角線上的元素為，則， （）因此,且只有時,這時。這說明最小二乘估計量是最優線性無偏估計量。三、 殘差和隨機擾動項方差的估計在參數估計量的方差和標準差的表達式及中,隨機擾動項未知,故需從殘差平方和出發對進行估計.（一）、殘差的性質殘差向量 （）記 ()則有 ()或

22、者 ()P是對稱的冪等矩陣(基本冪等矩陣),即有1. 殘差的期望為02.殘差的方差-協方差矩陣()這表明N個殘差間通常是相關的，因為 （）其中,是”帽子矩陣”的第行第列的元素.3 =0這一性質表明殘差與間是不相關的，即 ()（二）、殘差平方和的矩陣表示殘差平方和因為故殘差平方和是矩陣的主對角線上元素平方和，即矩陣的跡()（三）、方差的估計對兩邊求期望得()（矩陣的跡的性質：） 記則， 是的無偏估計。是隨機擾動項的無偏估計，或稱估計標準誤差。這樣參數估計量的方差、標準差、協方差分別可用其樣本方差、樣本標準差、樣本協方差加以估計。 ()()()定理： 當時，且與獨立。這一性質表明，當假定回歸模型中

23、相互獨立且時，而的估計與分布有關，且與是獨立的。此性質為模型的檢驗提供了依據。四、 多元線性模型的統計檢驗（一）、擬合優度檢驗1 總離差平方的分解及矩陣表示總離差平方和=ESS+RSS=回歸平方和+殘差平方和 () () () 2 樣本判別系數（判定系數） （），越接近于1，回歸直線擬合程度越高，說明一組自變量對因變量Y的解釋程度。3 校正可決系數從的表達式可以看出，的大小還受到解釋變量個數k的影響.增大解釋變量的個數，將增大，回歸平方和增大，從而增大，由于增加個數引起的增大與擬合好壞無關，在變量個數k不同的模型之間比較擬合優度時，就不是一個合適的指標，必須加以調整。調整的思想是將殘差平方和與

24、總離差平方和之比的分子分母分別用各自的自由度去除，變成均方差之比，以剔除變量個數對擬合優度的影響。 定義校正系數為 ()或 （）消除了解釋變量個數的影響。從（）式可以看出，（1）當時，這意味著隨著自變量x的個數的增加，校正系數小于；（2）盡管總是非負的，但卻可能為負，若遇到為負的情形，可以認為其值為零。在實際應用中我們常常將它與F檢驗結合起來使用。（二）、相關系數檢驗相關系數是用來描述變量間的線性密切程度的一種數量指標，通常用或來表示。相關系數有簡單相關系數、復相關系數、偏相關系數。1 簡單相關系數簡單相關系數用來描述兩個變量間線性關系的密切程度的。如變量Y與X的簡單相關系數的計算公式為： （

25、）或 （2.2.60）2 復相關系數 復相關系數是用來描述變量Y與自變量之間線性相關程度的指標，其計算公式為： （2.2.61） (2.2.62）在此與可決系數的計算公式一樣，但說明一組自變量對因變量Y的解釋程度。，越大表明自變量所引起的變動越大，也就是自變量對Y的影響越大。說明Y與存在完全的線性關系，它們之間高度相關，表明y與無關，在大多數情況下，。3 偏相關系數在多數問題中，兩個變量之間的相關程度總要受到其他有關變量的影響，例如，某旅游地熱飲料的銷售量Y與該地區游客數量的關系要受到天氣條件的影響。這時Y與的簡單相關系數不能反映Y與的真實相關程度。如果要研究Y與的真實相關就必須剔除對它的影響

26、。在多元回歸分析中，當其他變量被固定后，給定的任兩個變量的相關系數，叫做偏相關系數，它是度量k+1個變量Y，之中任意兩個變量的線性相關程度，而這種線性相關是在去掉其余k-1個變量后任意非空子集合影響下的線性關系。特別是利用偏相關系數來度量Y與某一自變量之間的依賴關系。設k個自變量，每兩個自變量間及與因變量Y的影響的簡單相關系數矩陣為：r 簡單相關系數所構成的行列式為：其中 （2.2.63） （2.2.64）因變量Y與自變量的偏相關系數： （2.2.65）這里都是中元素的代數余子式，都是對稱行列式。下列給出一個遞推公式： 是剔除的影響后Y與的偏相關程度的度量。（三）、總體回歸方程的顯著性檢驗（F

27、檢驗）與一元回歸分析一樣，多元線性回歸模型的F檢驗就是檢驗總體回歸方程是否顯著，即檢驗假設： 若與之間線性關系顯著，就拒絕，否則就接受。具體步驟如下：（1） 建立假設：；不全為0（2） 列出方差分析表離差平方和名稱表達式自由度ESS=（3） 在H0成立的條件下，統計量由樣本觀測值，計算F值；（4） 檢驗：給定顯著性水平，查表得臨界值。若，拒絕H0，回歸方程顯著成立；若，接收H0，回歸方程不顯著。（四）、參數的顯著性檢驗t檢驗是檢驗解釋變量對因變量線性作用是否顯著的一種統計檢驗。雖然已經由F檢驗對總體回歸方程的顯著性作了檢驗，但在多元回歸分析中，總體回歸方程的顯著性還不能說明每個解釋變量對的影響

28、都是重要的。這就需要對每個解釋變量檢驗其對的線性作用是否顯著。即檢驗：若對的作用顯著就拒絕H0，否則就接收H0。具體步驟如下：（1） 建立假設：；（2） 在H0成立的條件下，統計量其中是中的主對角線上第個元素，根據樣本觀測值，計算t值；（3） 檢驗：給定顯著性水平，查表得臨界值。 若，就拒絕H0，對有顯著線性作用； 若，就接收H0，對的線性作用不顯著。五、預測多元線性回歸模型為根據樣本觀測值，利用最小二乘法已求得樣本回歸方程預測就是給定解釋變量樣本外的某一特定值向量對因變量值及進行估計。（一）、點預測由將代入可得,可作: 1、的個別值的預測 2、 的平均值的預測（二）、區間預測設是因變量觀測值向量與其預測值向量之差.則有將代替,得的標準差估計值可以證明,統計量即對于給定的顯著性水平,查分布表,可得臨界值,因變量個別值的預測區間: (2.2.66)同理可得均值的預測區間為 (2.2.67)六、多元線性回歸分析計算步驟及主要計算公式根據前幾節的內容可歸納多元線性回歸分析計算步驟及主要計算公式如下:1 由樣本觀測值，寫出，2 計算 3 計算最小二乘估計量4 計算殘差以及殘差平方和， 5 估計標準誤差6 計算可決系數和校正可決系數,作擬合優度檢驗7 計算