1、第二十八講奇妙的對稱對稱是一種客觀存在，一朵紅花、一片綠葉、一只色彩魔斕的蝴蝶等，最令人驚奇的就 是它們外形的幾何對稱性，自然界的對稱性可以在從亞原子粒子的結構到整個宇宙的結構的 每一個尺度上找到.對稱是一種美的標準，人類心智中的某種東西受對稱的吸引，對稱對我們的視覺有感染 力，影響我們對美的感受，建筑、繪畫廣泛地應用對稱.對稱是一個數學概念，我們熟悉的有代數中的對稱式、幾何中的軸對稱、中心對稱等， 更一般情況是，許多數學問題所涉及的對象具有對稱性，不僅包括幾何圖形中的對稱，而且泛指某些對象在有些方面如圖形、關系、地位等同彼此相對又相稱.對稱是一種解題方法，即解題時充分利用問題自身條件的某些對

2、稱性分析問題，在探 求幾何最值、代數式的化簡求值等方面有廣泛的應用.例題求解【例 1】 如圖， ABC 中，AC=BC=5，/ ACB=80 ,0 ABC 中一點，/ OAB=10 , / OBA=30 ，則線段 A0的長是.(第14屆“希望杯”邀請賽試題)思路點撥 OAB是一般三角形，作/ ACB的平分線，與7 / 70C,通過全等尋找與 A0相等的線段，促使問題的解決. 注 物理學家皮埃爾居里曾說，“結果與其原因一樣對稱.大干世界，許多事物都具有某種對稱性許多化學分子是對稱的，細胞結構是對稱的， 病毒往往也是對稱的，”對稱給人們以和諧均衡的羌感，完全的對稱是重復性的可預言的,人類在漫長的歲

3、月里，體驗著對稱，享受著對稱.求幾何量的最值問題常用方法有：(1) 應用幾何中的不等式性質，定理；(2) 對稱分析；代數法即著眼于揭示問題中變動元素的代數關系.【例2】如圖，正方形 ABCD的邊長為3, E在BC上，且BE=2 , P在BD上，則PE+PC的最小值為()(“新蕾杯”思路點撥 C、E兩點位置固定，從對稱性考慮，確定P點位置.【例3】現有一塊形如母子正方形的板材，木工師傅想先把它割成幾塊，然后適當拼接，制成某種特殊形狀的板面 (要求板材不能有剩余，拼接時不重疊、無空隙)，請你按下列要求幫助木工師傅分別設計一種方案：(1) 板面形狀為非正方形的中心對稱圖形；(2) 板面形狀為等腰梯形

4、；(3) 板面形狀為正方形.(1) 思路點撥問題(1)，由“中心對稱的四邊形是平行四邊形”想象出中心對稱的多邊形的大致形狀；問題(2)，先計算等腰梯形面積為 5,猜想等腰梯形的高，可能為 2，因此，上、F底的和應為5;問題，由正方形的面積為 5，計算出它的邊長應為.【例4】 已知a 1 -b2 bh -a2 =1，試確定a、b的關系.(第15屆江蘇省競賽題)思路點撥 有理化是解根式問題的基本思路，乘方、配方、換元、引入有理化因式等是有理化的常用方法.本例是一道膾炙人口的名題，引入與已知等式地位相對相稱的有理化因式，本例可獲得簡解.注 數學中的對稱，不僅指幾何圖形中的對稱，代數表示式中，若各個宇

5、母互相替代，表示式不變，也稱這個表示式關于這些字母是對稱的， 一個復雜的二元對稱式.都可以用最簡單 對稱式a b , ab表示.許多數學問題有著和諧的對稱美.對原題匹配一個與之相對的數學式，然后一起參與運算，這就是常說的“對稱性地處理具有對稱性的問題”，是數學解題中的一個一般性原則.用對稱法解幾何題的常見的方式有：(1)作出常見軸對稱圖形的對稱軸，或利用題設條件中的垂線、角平分線翻折造全等； 利用中點構造中心對稱圖形.【例5】 如圖，凸四邊形 ABCD的對角線AC、BD相交于0,且AC丄BD，已知0A 0C , OB 0D，比較BC+AD與AB+CD的大小.(“祖沖之杯”邀請賽試題 )思路點撥

6、 以AC為對稱軸，將部分圖形翻折，把相關線段集中到同一個三角形中去， 以便運用三角形三邊關系定理，這是解本例的關鍵.【例6】如圖，在 ABC中，AD是BC邊的中線，點 M在AB邊上，點 N在AC邊上，并且/ MDN=90 ，如果 BM2+CN2= DM2+DN2,求證：AD2=1（AB2 - AC2）.4（北京市競賽題）思路點撥 易想到勾股定理，需要把分散的條件加以集中，利用中點，構造中心對稱全等三角形.學力訓練1. 下面四個圖形中，從幾何圖形的性質考慮，哪一個與其他三個不同？請指出這個圖形，并 簡述你的理由.答：圖形 ;理由是： .（2003牛吉林省中考題）A/K A A 2. 如圖，兩點A

7、、B在直線MN外的同側，A到MN的距離AC=8 , B到MN的距離BD=5 ,CD = 4, P在直線MN上運動，則 PA-PB的最大值等于 .（第14屆“希望杯”邀請賽試題）3. 如圖，在等腰三角形 ABC中，/ C=90 , BC=2皿，如果以 AC的中點0為旋轉中心， 將這個三角形旋轉 180。，點B落在點B 處，那么 B 點與B點的原來位置相距cm.（第 2 題）（第 3 題）（第 4 題）4. 如圖，/ AOB=45。，角內有點 P, PO=10，在角的兩邊上有兩點 Q, R（均不同于O點）, 則厶PQR的周長的最小值為 .（2002年黃岡市中考題）5. 設將一張正方形紙片沿右圖中虛

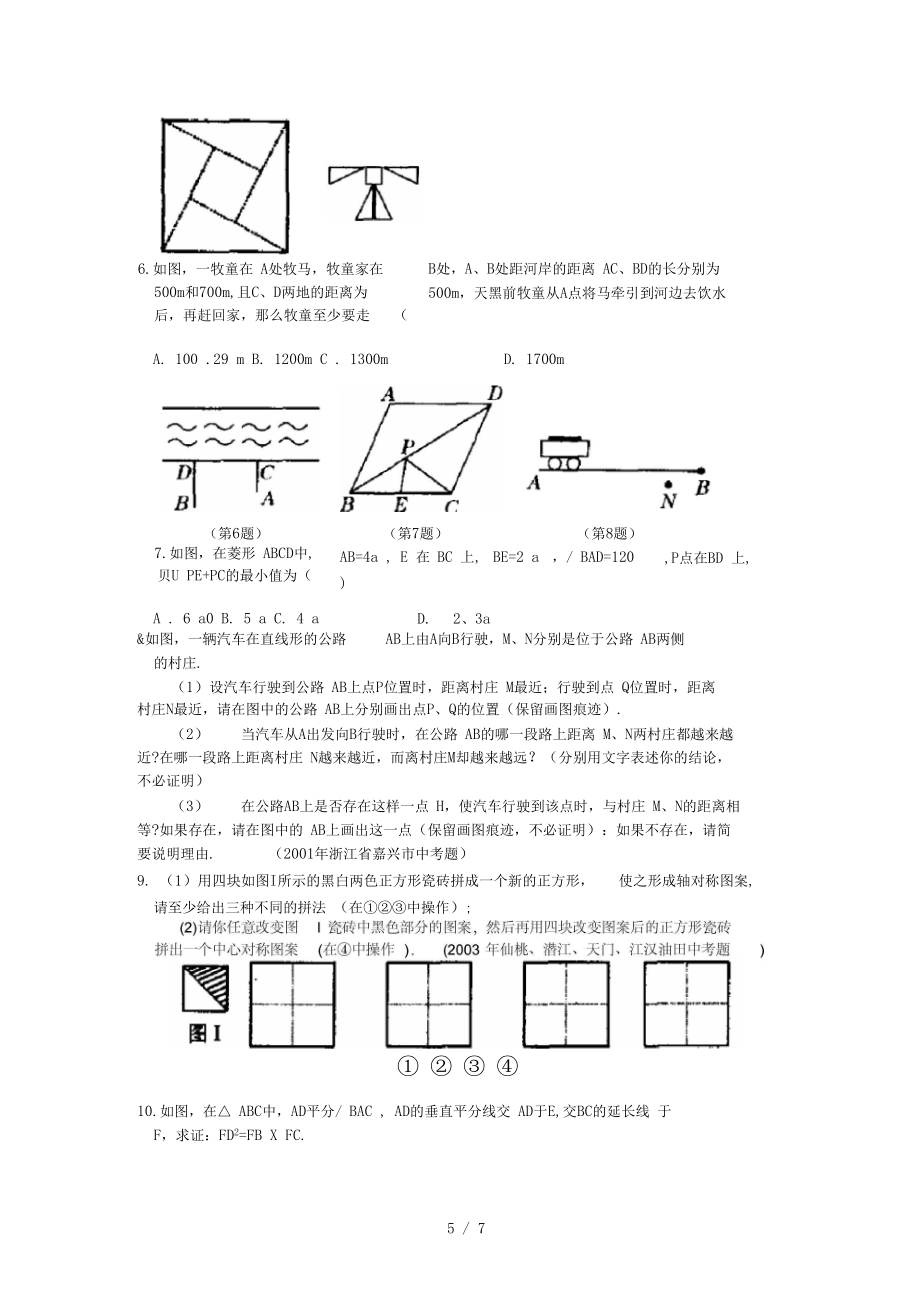
8、線剪開后，能拼成下列四個圖形，則其中是中心對稱圖形的是（）（2003平龍巖市中考題）6.如圖，一牧童在 A處牧馬，牧童家在500m和700m,且C、D兩地的距離為 后，再趕回家，那么牧童至少要走（B處，A、B處距河岸的距離 AC、BD的長分別為 500m，天黑前牧童從A點將馬牽引到河邊去飲水）A. 100 .29 m B. 1200m C . 1300mD. 1700m（第6題）（第7題）（第8題）7.如圖，在菱形 ABCD中,貝U PE+PC的最小值為（AB=4a , E 在 BC 上,)BE=2 a，/ BAD=120,P點在BD 上,A . 6 a0 B. 5 a C. 4 aD.2、3

9、a&如圖，一輛汽車在直線形的公路AB上由A向B行駛，M、N分別是位于公路 AB兩側的村莊.（1）設汽車行駛到公路 AB上點P位置時，距離村莊 M最近；行駛到點 Q位置時，距離 村莊N最近，請在圖中的公路 AB上分別畫出點P、Q的位置（保留畫圖痕跡）.（2）當汽車從A出發向B行駛時，在公路 AB的哪一段路上距離 M、N兩村莊都越來越 近?在哪一段路上距離村莊 N越來越近，而離村莊M卻越來越遠？（分別用文字表述你的結論， 不必證明）（3）在公路AB上是否存在這樣一點 H，使汽車行駛到該點時，與村莊 M、N的距離相等?如果存在，請在圖中的 AB上畫出這一點（保留畫圖痕跡，不必證明）：如果不存在，請簡

10、 要說明理由.（2001年浙江省嘉興市中考題）9. （1）用四塊如圖I所示的黑白兩色正方形瓷磚拼成一個新的正方形，使之形成軸對稱圖案,請至少給出三種不同的拼法 （在中操作）; 10.如圖，在 ABC中，AD平分/ BAC , AD的垂直平分線交 AD于E,交BC的延長線 于 F，求證：FD2=FB X FC.11.如圖，設Li和L2，是鏡面平行且鏡面相對的兩面鏡子，把一個小球放在之間，小球放在鏡L|中的像為A A 在鏡L2中的像為A，若L|、L2的距離為7,則AA （第15屆江蘇省競賽題）（第10題）（第11題）（第12題）（第13題）12 .如圖，設 M是厶ABC的重心，且 AM=3 , B

11、M=4 , CM=5，則 ABC的面積為13 .如圖，ABCD ABCD為長方體，AA=50cm , AB=40cm , AD=30cm，把上、下底面 都等分成3X 4個小正方形，其邊長均為 10cm，得到點E、F、G、H和E,、F,、G,、H，假設一只螞蟻每秒爬行2cm,則它從下底面 E點沿表面爬行至上底面 G,點至少要花時間秒.14無理數（V ,2）4的整數部分是 .（第12屆“希望杯”邀請賽試題）215當x等于丄，丄 ,1 , 1, 2, , ,1992, 1993時，計算代數式 丄石的值,1993199221 +x2再將所得的結果全部加起來，總和等于 .16. 一束光線經 3塊平面鏡反

12、射，反射的路線如圖所示，圖中字母表示相應的度數，已知 c=60 ，求d+e與x的值.n(r17.如圖，在厶ABC中，AD / BC ,已知/ ABC / ACB , P是AD上的任點，求證：AC+BPvAB+PC .R D18.如圖，矩形 ABCD 中，AB=20cm , BC=l0cm ,若在 AC、AB 上各取一點 M、N，使 BM+MN 的值最小，求這個最小值.A JjfB19.如圖，在 ABC中，D、E分別為BC、AC的中點，AD、BE相交于P,若/ BPD= /C,求證：以厶ABC三條中線為邊構成的三角形與厶 ABC相似.（2004年武漢市選拔賽試題）L !l Ji Is -J-B-

13、“ J PTl* 1 - 1F哼廠 4| I * * 吞 *L.JJ LJp#JRI 連的孚分蜒兀6 交 M 延扶線于 , JB ZCAB /CBA =/少5e+AEA4 甘(P+為 H/+沖即 AD+BOA3+CD靜餉JD 修 D 點英轉 180iCED.i1 BM-CE.AfiCE, MNbNE,jB MN=NE7 S+CNC+C-W+DNP,:.Z/VCE-SO%由業得/咼G-腫*故 AF +AC*=BC =1 即 AD1 = -r(ABz+AC1,4【學力訓練】I. 圖不是軸對稱圖昭.2.延KiJXMN點P運動到P點時I PAPEI =5為最大3. 254. 10# 分別菲P關TOA.

14、OB的對稱點M,N*連結0AQB交于Q.R.PQR符合衆杵.5. B *- C甘別作&A點義于河斥的對稱點E*連皿疋河岸于P fSi PB+PA=PB+ PF=BF 短連EF,jR BE尅D+M= 12O0tBF= /BEr+AF! = 500!+1200-1300 C m) 7, D AX 差于 BD 對稱.連 AE 交 BD 于 P,苴 AE丄BC. J/BAE=20PE+PCAE= /(4a)2-(2a)T =23 為星小.乩(I)分則過M, N作AH的垂線垂足P、Q即為所求的點；(卻當訊車從A向B行農時在為P這段路上離繭個村莊越來 越近I在PQiA段踣上，離村莊來越遠離村蟲N越來越近M

15、3)點H存在*連結胚比作戲段的中垂線，諭中垂線 與AB的交點即為所求的點H.9.曜IQ,連皓AFt則DF=AF需itAF = RFFU證明“ACFs色BFA即可11. 1412. 8 M tC BM AC 于 D,揮廷悅日D 至 E.使 DE-DM.連 EErAADM盈ACTJEtACMf 為 RtA.SiW 7耳加13螞蚊矗行的量複垢純只鏗過怏方協的3個表面且當將有關的3個表面展開在同一平面時， 其聶蝮路線為直線段由長方體的對稱性僅需考慮関種展開方雍(如圖由(1)有 egm v/2or+8or= 2o yrr.由)有 eu = yioT+9or= io y5zF由 io y2 20 帀，故最擁時何為*X20 717 = 10 顱14. (1+QGR1+我叩=+2施八加3 + 2找尸+(3-2握03-2#hO r 必八匚風又/BG