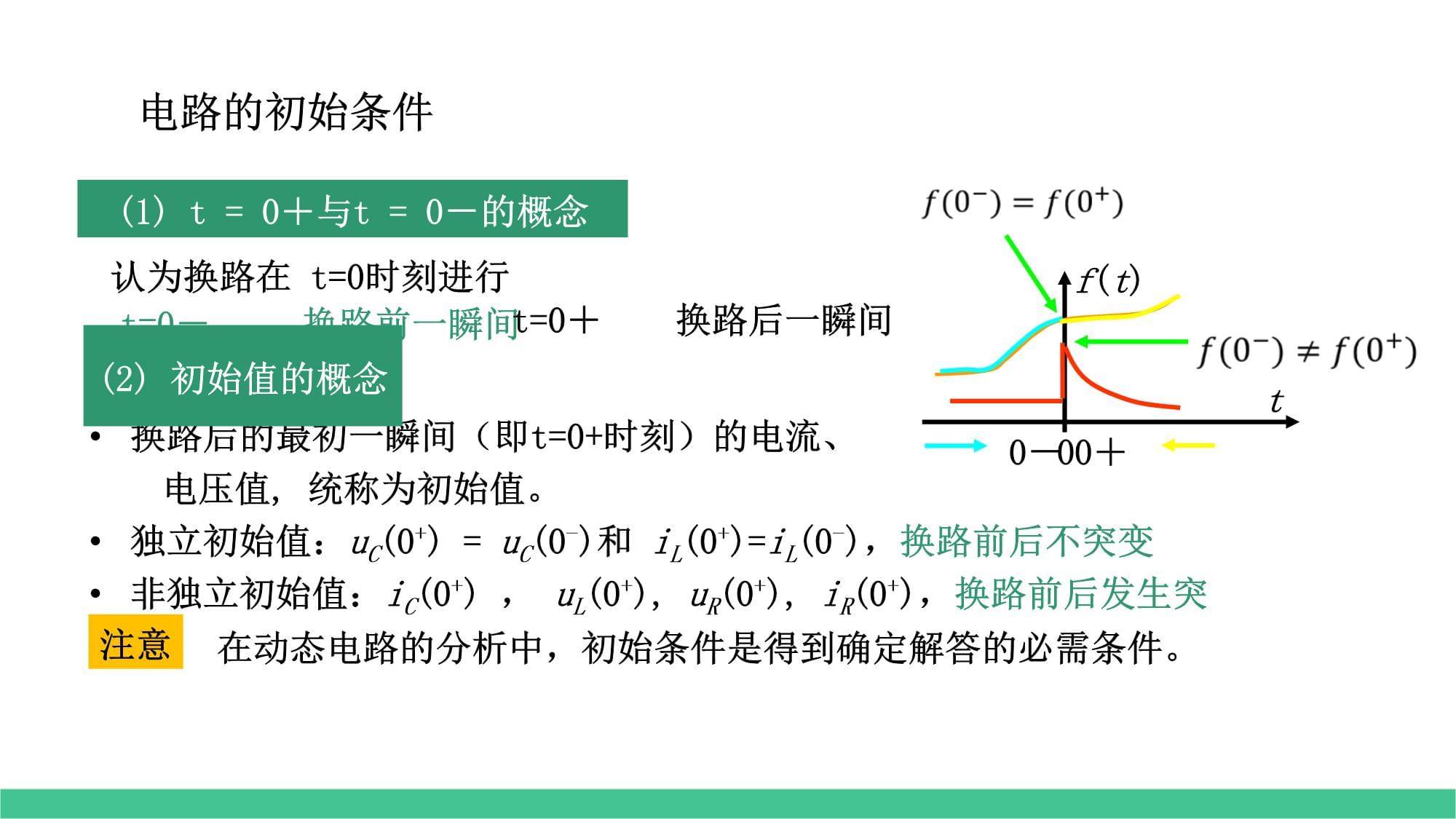
初始值的求取電路的初始條件(1)t=0＋與t=0－的概念認為換路在t=0時刻進行t=0－換路前一瞬間t=0＋換路后一瞬間0－0＋0tf(t)

換路后的最初一瞬間（即t=0+時刻）的電流、

電壓值,統稱為初始值。獨立初始值：uC(0+)=uC(0-)和iL(0+)=iL(0-)，換路前后不突變非獨立初始值：iC(0+)，uL(0+),uR(0+),iR(0+)，換路前后發生突變(2)初始值的概念在動態電路的分析中，初始條件是得到確定解答的必需條件。注意求初始值的步驟由換路前電路（一般為穩定狀態）求uC(0－)和iL(0－)；由換路定律求得獨立初始值：uC(0+)=uC(0-)和iL(0+)=iL(0-)；畫t=0+等效電路；由t=0+電路求非獨立變量的初始值。uC(0+)≠0時，電容用電壓源替代iL(0+)≠0時，電感用電流源替代換路后的電路（取0+時刻值，方向同原假定的電容電壓、電感電流方向）思考：uC(0+)=0時電容相當于什么？iL(0+)=0時電感相當于什么？短路開路1234舉例(2)由換路定律uC(0+)=uC(0－)=8Vt=0+等效電路

解：(1)由t=0－電路求uC(0－)或iL(0－)+-10V+uC-10k40kuC(0－)=8V(3)由t=0+等效電路求iC(0+)iC(0－-)=0iC(0+)例1：求iC(0+)電容開路電容用電壓源替代t=0-等效電路舉例例2：t=0時閉合開關k,求uL(0+)iL(0+)=iL(0－)=2A

iL+uL-L10VK1

4

+uL-10V1

4

t=0+電路2A(1)由t=0－電路求

電感用電流源替代

10V1

4

解：電感短路t=0-電路(2)由換路定律(3)由t=0+等效電路求uL(0+)舉例例3：已知iL(0)=0，uC(0)=0，試求S閉合瞬間，電路中所標示的各電壓、電流的初始值。解：根據換路定律可得可得t=0+時等效電路如下iL(0+)=iL(0–)=0，相當于開路uC(0+)=uC(0–)=0，相當于短路其他非獨立初始值為：

本節課程小結初始值（起始值）：電路中u、i在t=0+時的大小。1初始值求解要點：2（2）根據換路后的等效電路，應用換路定律確定其它非獨立初始值。（1）根據換路前一瞬間的電路，應用換路定律確定獨立初始值iL(0+）和uC(0+）。

換路定律什么是換路開關動作（閉合或斷開）致使電路結構或參數發生改變，稱為換路。1.電路接通、斷開電源2.電路中電源的升高或降低3.電路中元件參數的改變S5Vt=0＋與t=0－的概念認為換路在t=0時刻進行0－換路前一瞬間0＋換路后一瞬間0－0＋0tf(t)換路定律內容在換路瞬間，電容上的電壓、電感中的電流不能突變。注意：換路定律只對uC、iL有約束，電路中其他的電壓電流值可以發生躍變。

不能突變的原因自然界物體所具有的能量不能突變，能量的積累或釋放需要一定的時間。所以

不能突變的原因

換路應用1.RC換路應用開機前：開機后：

，一段時間后電容電壓逐漸升到正常工作電壓關機前：關機后：

為工作電壓為工作電壓，一段時間后電容電壓逐漸降到0可以延時通電、延時斷電開機延時：冰箱、空調的壓縮機啟動關機延時：樓梯燈、投影儀的風扇換路應用實際使用中（如直流電機、直流繼電器），要加保護措施，用續流二級管為電感提供放電回路，否則線圈兩端會產生高壓，對設備造成損壞。2.RL換路應用換路后的電流可能會轉化為大電壓傳統的汽車點火系統

R2=50?L=100mH

R1=4K?U=5V加以利用：給予防范：本節課程小結換路定律1換路應用2

動態電路要點一階動態電路和換路定理1初始值的求取2一階電路的零輸入響應3一階電路的零狀態響應4一階電路的全響應（三要素分析法）5動態電路含有電容和電感這樣的動態元件的電路稱動態電路。特點：當動態電路狀態發生改變時，需要經歷一個變化過程才能達到新的穩定狀態。這個變化過程稱為電路的過渡過程，又稱為暫態。過渡過程i

過渡時間為零0U1.無儲能元件——電阻電路電阻是耗能元件，其中電流隨電壓正比例變化，不存在暫態過程。過渡過程2.有儲能元件——RC電路

過渡狀態新的穩定狀態t1Uuct0暫態過程前一個穩定狀態

U過渡過程電容為儲能元件，它儲存的能量為電場能量，其大小為：

因為能量的存儲和釋放需要一個過程，所以含電容的電路存在過渡過程。電感也為儲能元件，它儲存的能量為磁場能量，其大小為：同理則含電感的電路也存在過渡過程產生暫態過程的必要條件電路中含有儲能元件（內因）電路內部含有儲能元件L、C，電路在換路時能量發生變化，而能量的儲存和釋放都需要一定的時間來完成。1電路發生換路（外因）2研究過渡過程的意義利如電子技術中常用它來產生各種波形；弊如在暫態過程發生的瞬間，可能出現過壓或過流，致使設備損壞，必須采取防范措施。過渡過程是一種自然現象，對它的研究很重要。過渡過程的存在有利有弊。動態電路的方程

應用KVL和元件的VCA得：+–uCUsRCi

(t=0)K1、RC電路

動態電路的方程2、RL電路

+–uLUsRLi

(t=0)K應用KVL和元件的VCA得：

動態電路的方程有源電阻電路一個動態元件只有一個動態元件，描述電路的方程是一階微分方程。一階電路（1）描述動態電路的電路方程為微分方程；（2）動態電路方程的階數等于電路中動態元件的個數；結論本節課程小結什么是電路1研究過渡過程的意義2一階動態電路的方程的列寫3

一階電路的零輸入響應一階電路的零輸入響應一階電路：在一個電路簡化后，只含有一個電容或電感元件的電路叫一階電路。實質：RC或RL電路的放電過程。零輸入響應：輸入信號為零，僅由初始狀態產生的響應。RC電路的零輸入響應+-SRU021+–

+–

換路前電路已處穩態t=0時開關S-->1換路后：開關合于位置1電容C經電阻R放電換路前：開關合于位置2

電容電壓uC的變化規律+-SRU021+–+–代入得一階線性常系數齊次微分方程(1)列

KVL方程

對元件列VCR方程

(2)解方程得電流及電阻電壓的變化規律tO

U0-U0iC

時間范圍？時間常數(2)物理意義令:單位：s(1)量綱

時間常數：決定電路暫態過程變化的快慢

時間常數(3)暫態時間

t0.368U00.135U00.050U00.018U00.007U00.002U0

當t=5τ

時，過渡過程基本結束，uC達到穩態值。本節課程小結

零輸入響應就是C或L的放電過程123

一階電路的零狀態響應RC電路的零狀態響應零狀態響應:儲能元件的初始能量為零，僅由電源激勵所產生的電路的響應。分析：在t=0時，合上開關s，此時,電路實為輸入一個階躍電壓u，如圖。與恒定電壓不同，其電壓u表達式實質：RC電路的充電過程。uC的變化規律一階線性常系數非齊次微分方程(1)列

KVL方程(2)解方程得

令uC(0-)=0sRU+_C+_iuc電容電壓uC的變化規律暫態分量穩態分量電路達到穩定狀態時的電壓-U+U僅存在于暫態過程中

63.2%U-36.8%Uto

穩態分量暫態分量

電流iC的變化規律和曲線

t練一練例：已知U=9V，R1=6kΩ，R2=3kΩ，C=1μF，uC(0-)=0V。求S閉合后的uC(t)。解：戴維南等效電路E+-Cu0RC

本節課程小結

零狀態響應就是C或L的充電過程134

2一階電路的全響應一階電路的全響應全響應：換路前電容儲能不為零，換路后電路有新的激勵接入電路。因為換路后的電路與零狀態響應的電路相同，所以微分方程相同。

一階電路的全響應全響應零輸入響應零狀態響應暫態響應穩態響應

求解得一階電路的三要素法根據經典法的推導,可得一階電路微分方程解的通用表達式：

穩態響應暫態響應

三要素三要素法分析要點

1根據換路定則得出：2

步驟

3

三要素法分析要點畫出換路后的等效電路（注意:在直流激勵的情況下,令C開路,L短路）； 1根據電路的定理和規則，求換路后所求未知數的穩態值。2穩態值??(∞)的計算步驟三要素法分析要點要由換路后的電路結構和參數計算。(同一電路中各物理量的τ