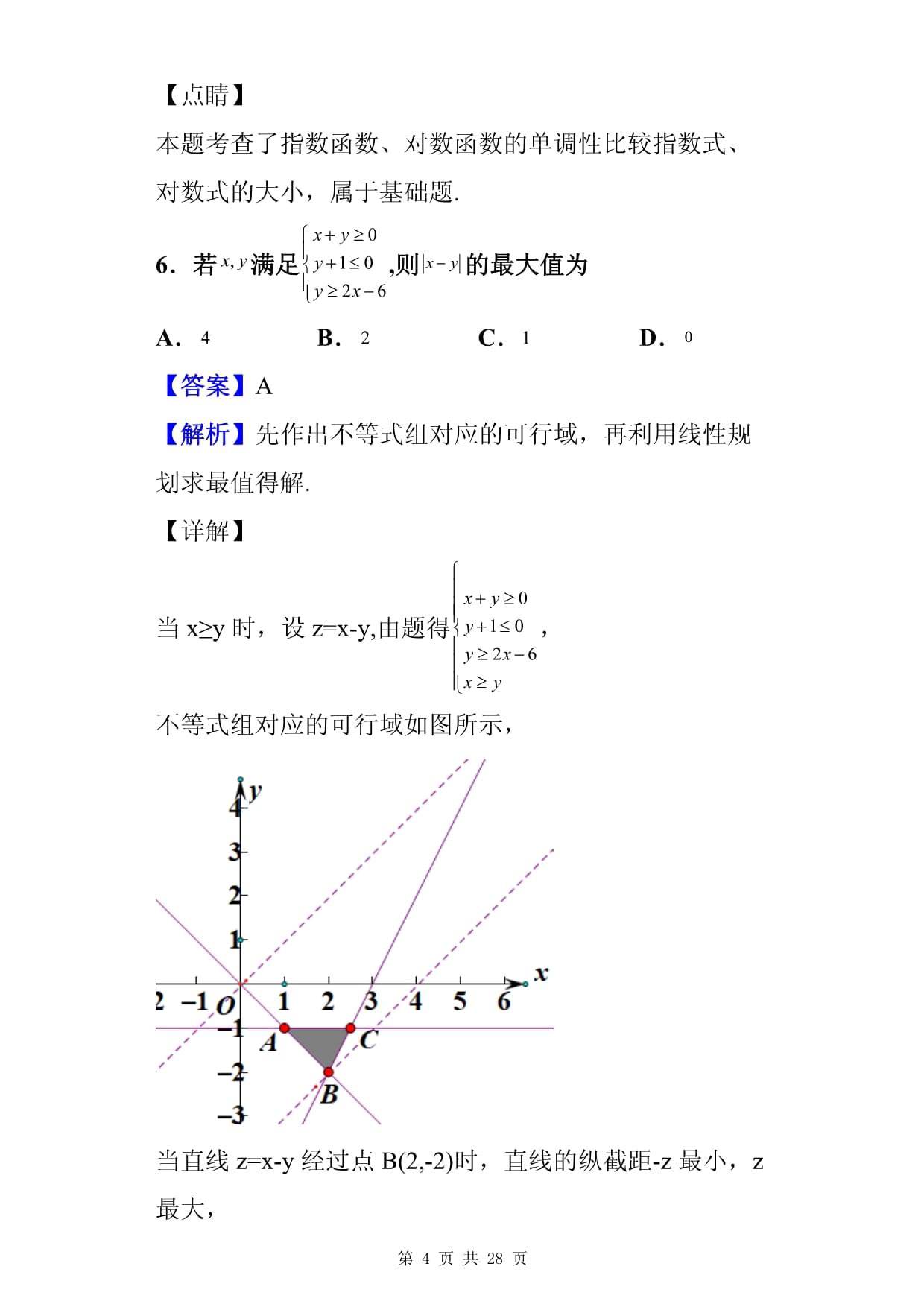
試卷第=page22頁，總=sectionpages33頁第Page\*MergeFormat1頁共NUMPAGES\*MergeFormat27頁吉林省長春市東北師大附中高三年級上學期第三次摸底數學（理）試題及答案一、單選題1．（）A． B． C． D．【答案】C【解析】利用復數的四則運算即可求解.【詳解】.故選：C【點睛】本題考查了復數的四則運算，屬于基礎題.2．已知集合，，則（）A． B． C． D．【答案】B【解析】求出集合，利用集合的交運算即可求解.【詳解】，，.故選：B【點睛】本題考查了集合的交運算，同時考查了一元二次不等式的解法以及絕對值不等式的解法，屬于基礎題.3．角的終邊與單位圓交于點，則（）A． B． C． D．【答案】A【解析】利用三角函數的定義可得，再由二倍角公式可得【詳解】由題意可得，所以.故選：A【點睛】本題考查了三角函數的定義以及二倍角公式，需熟記公式，掌握三角函數的定義是關鍵，屬于基礎題.4．已知向量，，設與的夾角為，則（）A． B． C． D．【答案】C【解析】根據向量的坐標運算求出向量，再利用向量數量積的坐標運算即可求解.【詳解】設，由，，可得，設與的夾角為，且則，所以.故選：C【點睛】本題考查了向量坐標表示、向量數量積的坐標運算，屬于基礎題.5．設，，，則的大小關系為（）A． B． C． D．【答案】B【解析】利用指數函數、對數函數的單調性即可求解.【詳解】由單調遞增，所以，即.由為增函數，則，所以，綜上可得.故選：B【點睛】本題考查了指數函數、對數函數的單調性比較指數式、對數式的大小，屬于基礎題.6．若滿足,則的最大值為A． B． C． D．【答案】A【解析】先作出不等式組對應的可行域，再利用線性規劃求最值得解.【詳解】當x≥y時，設z=x-y,由題得，不等式組對應的可行域如圖所示，當直線z=x-y經過點B(2,-2)時，直線的縱截距-z最小，z最大，此時z取最大值2-(-2)=4.當x＜y時，設z=y-x,由題得，不等式組沒有可行域，所以該情況不存在.故選：A【點睛】本題主要考查線性規劃求最值，意在考查學生對這些知識的理解掌握水平和分析推理能力.7．函數的圖像大致是（）A． B． C． D．【答案】A【解析】因為，所以去掉B,D;當時，所以去掉C,選A.8．設，則“”是“”的()A．充分而不必要條件 B．必要而不充分條件 C．充要條件 D．既不充分也不必要條件【答案】A【解析】運用絕對值不等式的解法和余弦函數的圖象和性質，化簡兩已知不等式，結合充分必要條件的定義，即可得到結論．【詳解】∵，，則，可得“”是“”的充分不必要條件，故選A.【點睛】本題考查充分必要條件的判斷，同時考查余弦函數的圖象和性質，運用定義法和正確解不等式是解題的關鍵，屬于基礎題．9．已知正項等比數列的前項和為，且，則的最小值為（）A． B． C． D．【答案】B【解析】根據是等比數列，由，即可得也是等比數列，結合基本不等式的性質即可求出的最小值.【詳解】是等比數列，，即，也是等比數列，且，，可得：，當且僅當時取等號，的最小值為.故選：B【點睛】本題考查了等比數列的前項和性質以及基本不等式求和的最小值，熟記等比數列的前項和性質是關鍵，屬于基礎題.10．已知函數的部分圖象如圖所示，則的單調遞增區間為（）A．B．C．D．【答案】C【解析】由圖可知函數的周期，進而根據周期公式求出，利用對稱軸以及的范圍可求出，再由正弦函數的單調遞增區間整體代入即可求解.【詳解】由圖可知，解得，所以，又，解得.，所以，所以，由，解得，所以的單調遞增區間為.故選：C【點睛】本題考查了由圖像求三角函數的解析式以及整體代入法求函數的單調區間，屬于基礎題.11．設函數的定義域為，滿足，且當時，.記當時，函數的極大值點從小到大依次記為并記相應的極大值為，則（）A． B． C． D．【答案】C【解析】根據以及極值點與極值的定義求出判斷分別為等差數列與等比數列，利用等差數列與等比數列的求和公式即可求解.【詳解】由，即，當時，，由題意可知，，當時，則，則，，當時，則，，則，，所以是以為首項，為公差的等差數列，是以為首項，為公比的等比數列，所以.故選：C【點睛】本題考查了三角函數的性質、極值點以及極值的定義、等差數列、等比數列的前項和公式，需熟記定義與公式，屬于中檔題.12．已知為銳角的外心，且三邊與面積滿足，若（其中是實數），則的最大值是（）A． B． C． D．【答案】D【解析】利用余弦定理以及三角形的面積公式求出，以邊所在的直線為軸，邊的垂直平分線為軸建立直角坐標系（為邊的中點），由外接圓的性質可得,由，不妨設外接圓的半徑，則,可得的坐標，設，則的外接圓的方程為：，利用向量的坐標運算可得，從而求出，代入外接圓方程可得，再利用基本不等式即可求解.【詳解】由，可知，解得，所以，如圖所示，以邊所在的直線為軸，邊的垂直平分線為軸建立直角坐標系（為邊的中點）由外接圓的性質可得,由，不妨設外接圓的半徑，則,，,，則的外接圓的方程為：，，，，，否則三點共線，由圖可知不可能的.可化為，代入的外接圓的方程可得，化為，化為，解得或，又，所以，所以的最大值為.故選：D【點睛】本題考查了余弦定理、三角形的面積公式、向量的坐標運算以及基本不等式求最值，綜合性比較強，屬于難題.二、填空題13．曲線在點處的切線方程為__________．【答案】【解析】由題可判斷出點在曲線上，所以通過求導求出切線的斜率，把斜率和點代入點斜式方程即可．【詳解】∵點（0，1）在曲線上，又由題意，，∴斜率k＝，∴所求方程為：，即y＝x+1．故答案為：．【點睛】本題考查導數的幾何意義的應用，屬于基礎題．14．如圖，正六邊形的邊長為，記，從點?????這六點中任取兩點為向量的起點和終點，則的最大值為______.【答案】2【解析】向量的數量積最大，需要兩個向量的模以及兩個向量的夾角的余弦函數值的乘積取得最大值即可.【詳解】由題意可知：則，由圖可知時，所以，故的最大值為2.故答案為：2【點睛】本題考查了向量數量積的定義，掌握向量數量積的定義是關鍵，屬于基礎題.15．公元前世紀，古希臘的畢達哥拉斯學派研究過正五邊形和正十邊形的作圖方法，發現了黃金分割，其比值為方程的正根，這一數值也可以表示為，則______.【答案】【解析】利用誘導公式以及二倍角的余弦公式即可求解.【詳解】.故答案為：【點睛】本題考查了誘導公式以及二倍角的余弦公式，需熟記公式，屬于基礎題.16．已知函數若存在實數，使得成立，則實數的取值范圍是______.【答案】【解析】由已知條件令可得，分離參數可得，令，求出的值域即可求解.【詳解】，且令，，即，從而可得，令，則，令，則，因為，所以，即在上為增函數，所以，即，所以，當時，，當時，，所以在上單調遞減，在上單調遞增，所以，所以，實數的取值范圍是.故答案為：【點睛】本題考查了導數在求函數最值中的應用，考查了分離參數法求參數的取值范圍，屬于難題.三、解答題17．已知數列的前項和為，且滿足，.（Ⅰ）求數列的通項公式；（Ⅱ）數列滿足，記數列的前項和為，求證.【答案】（Ⅰ）（Ⅱ）證明見解析【解析】（Ⅰ）根據與的關系，可得，從而判斷為等比數列，利用等比數列的通項公式即可求解.（Ⅱ）由（Ⅰ）得，，利用等差數列的求和公式可得，再利用裂項求和法可求出，令，易知單調遞增，借助函數的單調性即可求解.【詳解】（Ⅰ）因為，①當時，，②由①-②得，即，當時，，，所以數列為等比數列，其首項為，公比為，所以；（Ⅱ）由（Ⅰ）得，，所以，所以，所以令，易知單調遞增，所以，即，所以.【點睛】本題考查了與的關系、等比數列的通項公式、等差數列的前項和公式、裂項求和法以及函數的單調性求值域，綜合性比較強，屬于中檔題.18．如圖，在中，內角的對邊分別為，已知，點在邊上.（Ⅰ）求角；（Ⅱ）若，，且的面積與的面積之比為，求.【答案】（Ⅰ）（Ⅱ）【解析】（Ⅰ）利用正弦定理邊化角可得，再利用兩角和的正弦公式的逆應用即可求解.（Ⅱ）在中，，，從而可得，進而求出，在中，由正弦定理可得，根據的面積與的面積之比為，可得，在中，利用余弦定理即可求解.【詳解】（Ⅰ）由題意，∵，由正弦定理可得，即，∴，在中，，∴.∴，又在中，，∴.（Ⅱ）在中，，，∴.由（Ⅰ）可知，∴，在中，由正弦定理可得，∵的面積與的面積之比為，∴，∴.在中，由余弦定理可得，∴【點睛】本題考查了正弦定理、余弦定理解三角形，需熟記定理，屬于中檔題.19．如圖，三棱柱的側面是正方形，平面平面，，，點在上，，是的中點.（Ⅰ）求證：平面；（Ⅱ）判斷平面與平面是否垂直，直接寫出結論，不必說明理由；（Ⅲ）求二面角的余弦值.【答案】（Ⅰ）證明見解析（Ⅱ）平面平面（Ⅲ）【解析】（Ⅰ）連結交于，因為為中點，所以，利用線面平行的判定定理即可證出（Ⅱ）首先利用面面垂直的判定定理即可得出結論.（Ⅲ）建立空間直角建立坐標系，分別求出平面的一個法向量、平面的一個法向量，利用空間向量的數量積即可求解.【詳解】（Ⅰ）如圖所示，連結交于，因為為中點，所以，又因為平面,平面,所以平面.（Ⅱ）平面平面.（Ⅲ）如圖建立坐標系，設，，，設平面的一個法向量為，則，，令，則，同理可得平面的一個法向量為，所以，因為二面角為銳二面角，所以求二面角的余弦值為.【點睛】本題考查了線面平行的判定定理、面面垂直的判定定理以及空間向量法求二面角，考查了推理能力以及空間想象能力，屬于中檔題.20．已知的兩個頂點的坐標分別為，，且所在直線的斜率之積等于，記頂點的軌跡為.（Ⅰ）求頂點的軌跡的方程；（Ⅱ）若直線與曲線交于兩點，點在曲線上，且為的重心（為坐標原點），求證：的面積為定值，并求出該定值.【答案】（Ⅰ）（Ⅱ）證明見解析，定值為.【解析】（Ⅰ）設，根據題意列方程即可求解.（Ⅱ）設，，，由為的重心，可得，從而，，將直線與橢圓方程聯立整理利用韋達定理求出點坐標，代入橢圓方程可得，再利用弦長公式以及三角形的面積公式即可求解.【詳解】（Ⅰ）設，因為點的坐標為，所以直線的斜率為同理，直線的斜率為由題設條件可得，.化簡整理得，頂點的軌跡的方程為：.（Ⅱ）設，，，因為為的重心，所以，所以，，由得，，，，，∴，又點在橢圓上，所以，∴，因為為的重心，所以是的倍，，原點到直線的距離為，.所以，所以，的面積為定值，該定值為.【點睛】本題考查了直接法求曲線的軌跡方程、直線與橢圓的位置關系，考查了學生的計算能力，屬于中檔題.21．已知函數，.（Ⅰ）若為函數的極小值點，求的取值范圍，并求的單調區間；（Ⅱ）若，，求的取值范圍.【答案】（Ⅰ），的遞減區間和，遞增區間為，（Ⅱ）【解析】（Ⅰ）首先求出函數導數，分類討論或，判斷的正負即可求解.（Ⅱ）令，且，求出，令，且，求出在上單調遞增，進而分類討論或，求出的單調區間，即可求出的單調區間，判斷的正負即可求解.【詳解】（Ⅰ）由題意知：，且，若，即時，當，，所以不可能為的極小值點；若，即時，令；令或，所以的遞減區間和，遞增區間為，所以為函數的極小值點，綜上：，的遞減區間和，遞增區間為.（Ⅱ）令，則，，令，則，因為，令，則，，所以在上單調遞增，所以，（1）當，即時，，，所以在上單調遞增，所以對恒成立.所以恒成立，所以在上單調遞增，所以，，符合題意；（2）當，即時，因為，又且，又在上連續且單調遞增，所以存在，使得，此時，當時，，所以單調遞減，所以，所以，所以在單調遞減，所以，，矛盾，舍去.綜上：.【點睛】本題考查了導數在研究函數單調性以及導數在研究不等式恒成立中的應用，考查了轉化與化歸的思想、分析問題與解決問題的能力，屬于難題.22．在直角坐標系中，以坐標原點為極點，軸正半軸為極軸建立極坐標系，已知直線的極坐標方程為，曲線的參數方程為（為參數，）.（Ⅰ）當時，判斷直線與曲線的位置關系；（Ⅱ）設直線與軸的交點為，且與曲線交于兩點，且，求的值.【答案】（Ⅰ）直線與曲線相切（Ⅱ）【解析】（Ⅰ）將極坐標方程以及參數方程化為普通方程，再利用點到直線的距離公式即可判斷.（Ⅱ）由（Ⅰ）知，點坐標為，且直線的斜率為，直線的傾斜角為，將直線的參數方程與曲線的普通方程聯立，利用參數的幾何意義即可求解.【詳解】（Ⅰ）當時，曲線的參數方程為，∴曲線的普通方程為，表示以原點為圓心，為半徑的圓，∵，∴，∴直線的直角坐標方程為，即，∵到直線的距離為，∴直線與曲線相切；（Ⅱ）由（Ⅰ）知，點坐標為，且直線的斜率為，∴直線的傾斜角為，∴直線的參數方程為（為參數），曲線的普通方程為，將直線的參數方程代入曲線的普通方程，整理，