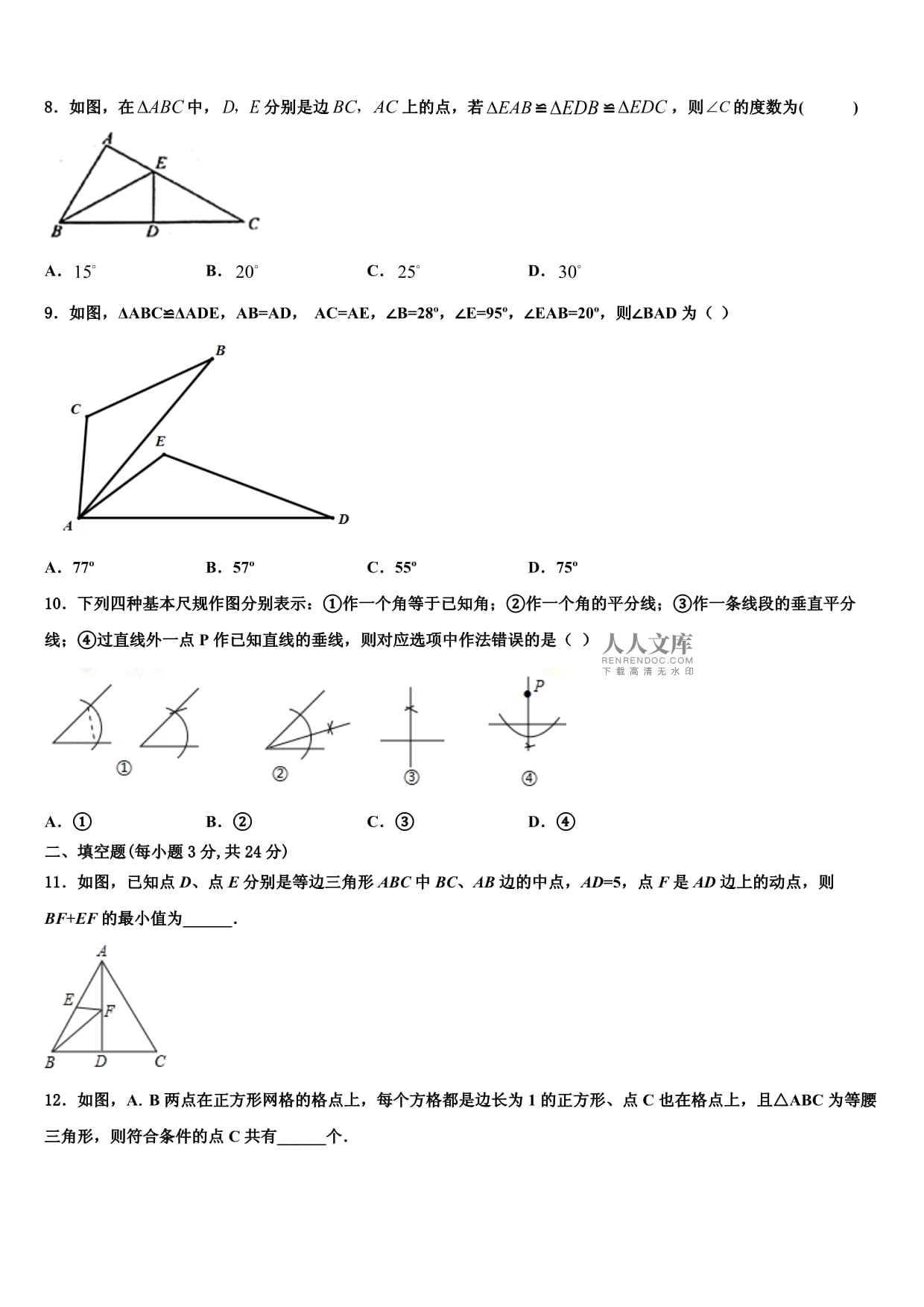
2024屆綿陽市重點中學數學八上期末質量檢測試題注意事項:1．答題前，考生先將自己的姓名、準考證號碼填寫清楚，將條形碼準確粘貼在條形碼區域內。2．答題時請按要求用筆。3．請按照題號順序在答題卡各題目的答題區域內作答，超出答題區域書寫的答案無效；在草稿紙、試卷上答題無效。4．作圖可先使用鉛筆畫出，確定后必須用黑色字跡的簽字筆描黑。5．保持卡面清潔，不要折暴、不要弄破、弄皺，不準使用涂改液、修正帶、刮紙刀。一、選擇題(每小題3分,共30分)1．的算術平方根是（）A． B． C．4 D．22．將分式中的的值同時擴大2倍，則分式的值（）A．擴大2倍 B．縮小到原來的C．保持不變 D．無法確定3．如果數據x1，x2，…，xn的方差是3，則另一組數據2x1，2x2，…，2xn的方差是（）A．3 B．6 C．9 D．124．如圖，已知每個小方格的邊長為1，A，B兩點都在小方格的頂點上，請在圖中找一個頂點C，使△ABC為等腰三角形，則這樣的頂點C有（）A．8個 B．7個 C．6個 D．5個5．下列長度的三條線段，能構成直角三角形的是（）A．8，9，10 B．1.5，5，2 C．6，8，10 D．20，21，326．估計的值約為()A．2.73 B．1.73 C．﹣1.73 D．﹣2.737．已知三角形三邊長3，4，，則的取值范圍是（）A． B． C． D．8．如圖，在中，分別是邊上的點，若≌≌，則的度數為()A． B． C． D．9．如圖，ΔABC≌ΔADE，AB=AD，AC=AE，∠B=28o，∠E=95o，∠EAB=20o，則∠BAD為（）A．77o B．57o C．55o D．75o10．下列四種基本尺規作圖分別表示：①作一個角等于已知角；②作一個角的平分線；③作一條線段的垂直平分線；④過直線外一點P作已知直線的垂線，則對應選項中作法錯誤的是（）A．① B．② C．③ D．④二、填空題(每小題3分,共24分)11．如圖，已知點D、點E分別是等邊三角形ABC中BC、AB邊的中點，AD=5，點F是AD邊上的動點，則BF+EF的最小值為______．12．如圖，A．B兩點在正方形網格的格點上，每個方格都是邊長為1的正方形、點C也在格點上，且△ABC為等腰三角形，則符合條件的點C共有______個．13．如圖，矩形ABCD中，AB=3，對角線AC，BD相交于點O，AE垂直平分OB于點E，則AD的長為____________．14．如圖，已知方格紙中是4個相同的小正方形，則的度數為______.15．在實數范圍內分解因式：____．16．如圖：在中，，平分，平分外角，則__________．17．因式分解x-4x3=_________．18．如圖，在平面直角坐標系中，有若干個橫坐標分別為整數的點，其順序按圖中“”方向排列，如，，，，，根據這個規律，第2019個點的坐標為___．三、解答題(共66分)19．（10分）如圖，CD∥EF，AC⊥AE，且∠α和∠β的度數滿足方程組（1）求∠α和∠β的度數．（2）求證：AB∥CD．（3）求∠C的度數．20．（6分）先化簡，再求值：（1+）÷，其中a是小于3的正整數．21．（6分）一輛汽車開往距離出發地的目的地，出發后第一小時內按原計劃的速度勻速行駛，一小時后以原來速度的1．5倍勻速行駛，并比原計劃提前到達目的地，設前一個小時的行駛速度為（1）直接用的式子表示提速后走完剩余路程的時間為（2）求汽車實際走完全程所花的時間．（3）若汽車按原路返回，司機準備一半路程以的速度行駛，另一半路程以的速度行駛()，朋友提醒他一半時間以的速度行駛,另一半時間以的速度行駛更快，你覺得誰的方案更快？請說明理由．22．（8分）如圖，四邊形中，，且，求的度數．23．（8分）計算：（1）；（2）24．（8分）某次學生夏令營活動，有小學生、初中生、高中生和大學生參加，共200人，各類學生人數比例見扇形統計圖．(1)參加這次夏令營活動的初中生共有多少人？(2)活動組織者號召參加這次夏令營活動的所有學生為貧困學生捐款．結果小學生每人捐款5元，初中生每人捐款10元，高中生每人捐款15元，大學生每人捐款20元．問平均每人捐款是多少元？(3)在(2)的條件下，把每個學生的捐款數額(以元為單位)——記錄下來，則在這組數據中，眾數是多少？25．（10分）已知等腰三角形周長為10cm，腰BC長為xcm，底邊AB長為ycm．（1）寫出y關于x的函數關系式；（2）求自變量x的取值范圍；（3）用描點法畫出這個函數的圖象．26．（10分）如圖，在平面直角坐標系中，已知A（4，0）、B（0，3）．（1）求AB的長為____．（2）在坐標軸上是否存在點P，使△ABP是等腰三角形？若存在，請直接寫出點P坐標；若不存在，請說明理由．

參考答案一、選擇題(每小題3分,共30分)1、D【分析】先化簡，再求的算術平方根即可．【題目詳解】=4，4的算術平方根是1，的算術平方根1．故選擇：D．【題目點撥】本題考查算數平方根的算數平方根問題，掌握求一個數的算術平方根的程序是先化簡這個數，再求算術平方根是解題關鍵．2、A【分析】根據已知得出，求出后判斷即可．【題目詳解】解：將分式中的、的值同時擴大2倍為，即分式的值擴大2倍，故選：A．【題目點撥】本題考查了分式的基本性質的應用，主要考查學生的理解能力和辨析能力．3、D【分析】先求出另一組數據的平均數，然后再利用方差公式求出方差，找到與給定的一組數據的方差之間的關系，則答案可解．【題目詳解】設數據x1，x2，…，xn的平均數為，方差為，則，，則另一組數據的平均數為，方差為：故選：D．【題目點撥】本題主要考查平均數和方差的求法，掌握平均數和方差的求法是解題的關鍵．4、A【分析】分AB為腰和為底兩種情況考慮，畫出圖形，即可找出點C的個數．【題目詳解】解：當AB為底時，作AB的垂直平分線，可找出格點C的個數有5個，當AB為腰時，分別以A、B點為頂點，以AB為半徑作弧，可找出格點C的個數有3個；∴這樣的頂點C有8個．故選A．【題目點撥】本題考查了等腰三角形的判定，解題的關鍵是畫出圖形，利用數形結合解決問題．5、C【分析】根據勾股定理的逆定理對各選項進行逐一判斷即可．【題目詳解】A、由于82＋92≠102，不能構成直角三角形，故本選項不符合題意；B、由于1.52＋22≠52，不能構成直角三角形，故本選項不符合題意；C、由于62＋82＝102，能構成直角三角形，故本選項符合題意；D、由于202＋212≠322，不能構成直角三角形，故本選項不符合題意；故選：C．【題目點撥】本題考查的是勾股定理的逆定理，即如果三角形的三邊長a，b，c滿足a2＋b2＝c2，那么這個三角形就是直角三角形．6、B【分析】先求出的范圍，即可求出答案．【題目詳解】解：∵1＜＜2，∴的值約為1．73，故選：B．【題目點撥】本題考查近似數的確定，熟練掌握四舍五入求近似數的方法是解題的關鍵．7、C【分析】根據三角形三邊的關系即可得出結論【題目詳解】解：∵三角形的三邊長分別是x，3，4，

∴x的取值范圍是1＜x＜1．

故選：C【題目點撥】此題考查了三角形的三邊關系：三角形任意兩邊之和大于第三邊，任意兩邊之差小于第三邊．8、D【分析】根據全等三角形的性質求得∠BDE=∠CDE=90°，∠AEB=∠BED=∠CED=60°，即可得到答案.【題目詳解】∵≌,∴∠BDE=∠CDE，∵∠BDE+∠CDE=180°，∴∠BDE=∠CDE=90°，∵≌≌，∴∠AEB=∠BED=∠CED，∵∠AEB+∠BED+∠CED=180°，∴∠AEB=∠BED=∠CED=60°，∴∠C=90°-∠CED=30°，故選：D.【題目點撥】此題考查了全等三角形的性質：全等三角形的對應角相等，以及平角的性質.9、A【解題分析】試題分析：∵△ABC≌△ADE，∴∠B=∠D=28°，又∵∠D+∠E+∠DAE=180°，∠E=95°，∴∠DAE=180°﹣28°﹣95°=57°，∵∠EAB=20°，∴∠BAD=∠DAE+∠EAB=77°．故選A．考點：全等三角形的性質10、C【解題分析】試題解析：①作一個角等于已知角的方法正確；②作一個角的平分線的作法正確；③作一條線段的垂直平分線缺少另一個交點，作法錯誤；④過直線外一點P作已知直線的垂線的作法正確．故選C．考點：基本作圖.二、填空題(每小題3分,共24分)11、5【分析】找到點E關于AD的對稱點E’,根據對稱得BF+EF=BE’，利用等邊三角形三線合一性質證明AD=BE’即可求出結果.【題目詳解】如下圖,作點E關于AD的對稱點E’,∵△ABC是等邊三角形,E為AB的中點,∴E’是線段AC的中點,∴AD垂直平分EE’,EF=E’F即BF+EF=BE’,又∵D是BC中點,∴AD=BE’=5（等邊三角形三線相等）,【題目點撥】本題考查了等邊三角形三線合一性質,圖形對稱的實際應用,中等難度,證明BF+EF=AD是解題關鍵.12、9【解題分析】根據已知條件，可知按照點C所在的直線分兩種情況：①點C以點A為標準，AB為底邊；②點C以點B為標準，AB為等腰三角形的一條邊．解：①點C以點A為標準，AB為底邊，符合點C的有5個；②點C以點B為標準，AB為等腰三角形的一條邊，符合點C的有4個．所以符合條件的點C共有9個．此題考查了等腰三角形的判定來解決特殊的實際問題，其關鍵是根據題意，結合圖形，再利用數學知識來求解．注意數形結合的解題思想．13、【解題分析】試題解析：∵四邊形ABCD是矩形，

∴OB=OD，OA=OC，AC=BD，

∴OA=OB，

∵AE垂直平分OB，

∴AB=AO，

∴OA=AB=OB=3，

∴BD=2OB=6，

∴AD=．【題目點撥】此題考查了矩形的性質、等邊三角形的判定與性質、線段垂直平分線的性質、勾股定理；熟練掌握矩形的性質，證明三角形是等邊三角形是解決問題的關鍵．14、90o【分析】首先證明三角形全等，根據全等三角形的性質可得對應角相等，再由余角的定義和等量代換可得∠1與∠2的和為90°.【題目詳解】解：如圖，根據方格紙的性質，在△ABD和△CBE中，∴△ABD≌△CBE（SAS），∴∠1=∠BAD，∵∠BAD+∠2=90°，∴=90°.故答案為：90°.【題目點撥】此題主要考查了全等圖形，關鍵是掌握全等三角形的判定和性質．15、【分析】將原式變形為，再利用平方差公式分解即可得．【題目詳解】===，故答案為：．【題目點撥】本題主要考查實數范圍內分解因式，解題的關鍵是熟練掌握完全平方公式和平方差公式．16、【分析】先根據角平分線的定義可得到，，再根據三角形的外角性質得到，進而等量代換可推出，最后根據三角形的外角性質得到進而等量代換即得．【題目詳解】∵平分∴∵平分外角∴∵的外角∴∵的外角∴∴∵∴故答案為：．【題目點撥】本題主要考查了外角性質及角平分線的定義，利用三角形的外角等于和它不相鄰的內角之和轉化角是解題關鍵．17、．【分析】先提取公因式，然后再用平方差公式進行因式分解即可．【題目詳解】解：故答案為：．【題目點撥】本題考查綜合提公因式和公式法進行因式分解，掌握平方差公式和完全平方公式的結構正確計算是本題的解題關鍵．18、（45,6）【分析】根據圖形推導出：當n為奇數時，第n個正方形每條邊上有（n+1）個點，連同前邊所有正方形共有（n+1）2個點，且終點為（1，n）；當n為偶數時，第n個正方形每條邊上有（n+1）個點，連同前邊所以正方形共有（n+1）2個點，且終點為（n＋1，0）.然后根據2019=452－6，可推導出452是第幾個正方形連同前邊所有正方形共有的點，最后再倒推6個點的坐標即為所求.【題目詳解】解：由圖可知：第一個正方形每條邊上有2個點，共有4=22個點，且終點為（1,1）；第二個正方形每條邊上有3個點，連同第一個正方形共有9=32個點，且終點為（3,0）；第三個正方形每條邊上有4個點，連同前兩個正方形共有16=42個點，且終點為（1,3）；第四個正方形每條邊上有5個點，連同前兩個正方形共有25=52個點，且終點為（5,0）；故當n為奇數時，第n個正方形每條邊上有（n+1）個點，連同前邊所有正方形共有（n+1）2個點，且終點為（1，n）；當n為偶數時，第n個正方形每條邊上有（n+1）個點，連同前邊所以正方形共有（n+1）2個點，且終點為（n＋1，0）.而2019=452－6n+1=45解得：n=44由規律可知，第44個正方形每條邊上有45個點，且終點坐標為（45,0），由圖可知，再倒著推6個點的坐標為：（45,6）.故答案為:（45,6）.【題目點撥】此題考查的是圖形的探索規律題，根據圖形探索規律并歸納公式是解決此題的關鍵.三、解答題(共66分)19、（1）∠α和∠β的度數分別為55°，125°；（2）見解析；（3）∠C＝35°．【分析】（1）根據方程組，可以得到∠α和∠β的度數；

（2）根據（1）∠α和∠β的度數，可以得到AB∥EF，再根據CD∥EF，即可得到AB∥CD；

（3）根據AB∥CD，可得∠BAC+∠C=180°，再根據AC⊥AE和∠α的度數可以得到∠BAC的度數，從而可以得到∠C的度數．【題目詳解】解：（1），①﹣②，得3∠α＝165°，解得，∠α＝55°，把∠α＝55°代入②，得∠β＝125°，即∠α和∠β的度數分別為55°，125°；（2）證明：由（1）知，∠α＝55°，∠β＝125°，則∠α+∠β＝180°，故AB∥EF，又∵CD∥EF，∴AB∥CD；（3）∵AB∥CD，∴∠BAC+∠C＝180°，∵AC⊥AE，∴∠CAE＝90°，又∵∠α＝55°，∴∠BAC＝145°，∴∠C＝35°．【題目點撥】本題考查平行線的判定與性質，解答本題的關鍵是明確題意，利用數形結合的思想解答．20、a+2，1．【解題分析】試題分析：先把括號內通分，再把分子分母因式分解，接著把除法運算化為乘法運算后約分得到原式=a+2，然后根據a是小于1的正整數和分式有意義的條件得到a=1，再把a的值代入計算即可．試題解析：原式=?=a+2，∵a是小于1的正整數，∴a=1或a=2，∵a﹣2≠0，∴a=1，當a=1時，原式=1+2=1．21、（1）；（2）小時；（3）故朋友方案會先到達【分析】（1）根據題意即可用的式子表示提速后走完剩余路程的時間；（2）根據題意可以列出相應的分式方程，求出x，即可求出汽車實際走完全程所花的時間；（3）設出總路程和兩種方案所用時間，作比后利用不等式的性質比較兩種方案所用時間的大小．【題目詳解】（1）用的式子表示提速后走完剩余路程的時間為故答案為；（2）由題意可得，+1+=，解得，x＝60經檢驗x＝60時，1.5x≠0，∴x＝60是原分式方程的解，即原計劃行駛的速度為60km/h．∴汽車實際走完全程所花的時間為+1=小時；（3）設總路程s，司機自己的方案時間為t1，朋友方案時間t2，則t1=∴t2=，∴因為m≠n，所以，（m＋n）2＞4mn，所以＞1，所以，＞1．t1＞t2．故朋友方案會先到達．【題目點撥】本題考查分式方程的應用，解題的關鍵是明確題意，找出所求問題需要的條件，注意要驗根．22、135°【分析】連接BD，根據勾股定理的逆定理得出△ABD為直角三角形，進而解答即可．【題目詳解】解：如圖，連接BD，∵BC=CD=2，∠C=90°，

在Rt△BCD中，BD2=BC2+DC2=8，∠BDC=∠DBC=45°．

在△ABD中，∵AB2+BD2=12+8=9=32=AD2，

∴△ABD為直角三角形，

故∠ABD=90°，

∴∠ABC=∠ABD+∠DBC=90°+45°=135°．【題目點撥】本題考查的是勾股定理、勾股定理的逆定理，根據題意作出輔助線，構造出直角三角形是解答此題的關鍵．23、（1）；（2）【分析】（1）首先將各項二次根式化到最簡，然后進行加減計算即可；（2）首先去括號，然后進行加減計算即可.【題目詳解】（1）原式==；（2）原式===【題目點撥】此題主要考查二次根式的混合運算，熟練掌握運算法則，即可解題.24、(1)80人；(2)11.5元；(3)10元.【解題分析】試題分析：（1）參加這次夏令營活動的初中生所占比例是：1﹣10%﹣20%﹣30%=40%，就可以求出人數．（2）小學生、高中生和大學生的人數為200×20%=40，200×30%=60，200×10%=20，根據平均數公式就可以求出平均數．（3）因為初中生最多，所以眾數為初中生捐款數．試題解析：解：（1）參加這次夏令營活動的初中生共有200×（1-10%-20%-30%）=80人；

（2）小學生、高中生和大學生的人數為200×20%=40，200×30%=60，200×10%=20，

所以平均每人捐款==11.5（元）；

（3）因為初中生最多，所以眾數為10（元）．25、（1）y＝10﹣2x；（2）2.5＜x＜5；（3）見解析．【分析】（1）根據等腰三角形的周長公式求出y與x的函數關系式；

（2）求自變量x的取值范圍，要注意三角形的特點，兩邊之和大于第三邊