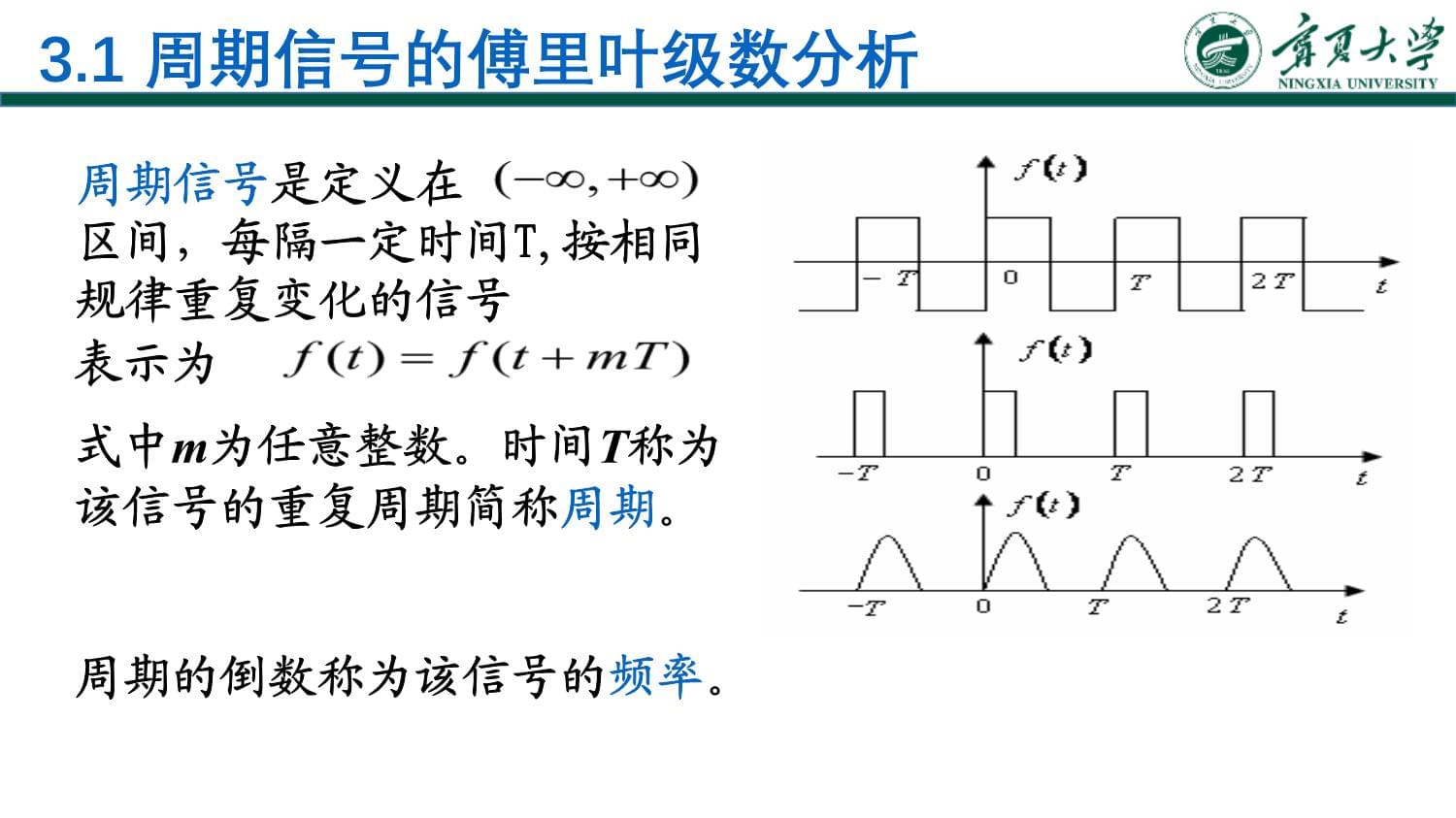
第3章連續時間信號與系統的頻域分析本章將以正弦函數（正弦和余弦函數可統稱為正弦函數）或虛指數函數為基本信號；任意信號可表示為不同頻率的正弦函數或虛指數函數之和（對于周期信號）或積分（對于非周期信號）。把信號表示為不同頻率正弦分量或虛指數分量的和稱為信號的頻域分析，也稱信號的譜分析。用頻譜分析的觀點來分析系統，稱為系統的頻域分析。3.1周期信號的傅里葉級數分析周期的倒數稱為該信號的頻率。周期信號是定義在區間，每隔一定時間T,按相同規律重復變化的信號表示為式中m為任意整數。時間T稱為該信號的重復周期簡稱周期。周期信號f(t)在區間可以展開成在完備正交信號空間中的無窮級數。如果完備的正交函數集是三角函數集或指數函數集，那么，周期信號所展開的無窮級數就分別稱為“三角形傅里葉級數”或“指數形傅里葉級數”，統稱傅里葉級數。需要指出，只有當周期信號滿足狄里赫利條件時才能展開成傅里葉級數。通常遇到的周期信號都滿足該條件，以后不再特別說明。3.1.1周期信號的分解1．信號分解為正交函數信號分解為正交函數的原理與矢量分解為正交矢量的概念相似。例：在平面上的矢量A在直角坐標中可以分解為x方向分量和y方向分量。如令，為各相應方向的正交單位矢量，則矢量A可寫為為便于研究矢量分解，將相互正交的單位矢量組成一個二維“正交矢量集”。這樣在此平面上的任意矢量都可用正交矢量集的分量組合表示。對于一個三維空間的矢量A，可以用一個三維正交矢量集的分量組合表示，它可寫為空間矢量正交分解的概念可以推廣到信號空間，在信號空間找到若干個相互正交的信號作為基本信號，使得信號空間中任一信號均可表示為它們的線性組合。如有定義在區間的兩個函數和，若滿足則稱和在區間內正交。如有n個函數，，…

，構成一個函數集，當這些函數在區間內滿足式中為常數，則稱此函數集為在區間的正交函數集。在區間內相互正交的n個函數構成正交信號空間。如果在正交函數集{，，…，}之外，不存在函數滿足等式則此函數集稱為完備正交函數集。也就是說，如能找到一個函數，使得上式成立，即與函數集{}的每個函數都正交，那么它本身就應屬于此函數集。顯然，不包含的集是不完備的。例如，三角函數集在區間組成正交函數集，而且是完備的正交函數集。這是因為集合在區間內也是正交函數集，但它是不完備的，因為還有許多函數，如，，…，也與此集合中的函數正交。復函數集，正交的定義

若復函數集{}（）在區間滿足則稱此復函數集為正交函數集。式中，為函數的共軛復函數。

復函數集{}（）在區間內是完備的正交函數集，式中。它在區間內滿足設有n個函數，，…

，在區間構成一個正交函數空間。將任一函數用n個正交函數的線性組合來近似，這可表示為2．周期信號的分解設有周期信號,它的周期是

T，角頻率可分解為式中的系數，稱為傅里葉系數

式中

是（）的偶函數，即有；而是（）的奇函數，即周期信號可以分解為各次諧波分量。表明:任何滿足狄里赫利條件的周期函數可分解為直流和許多余弦（或正弦）分量。其中第一項是常數項，它是周期信號中所包含的直流分量；式中第二項稱為基波或一次諧波，它的角頻率與原周期信號相同，是基波振幅，是基波初始相角，式中第三項稱為二次諧波，它的頻率是基波頻率的二倍。是二次諧波振幅，是其初始相角。依此類推，還有三次、四次、…等諧波。解：例

將圖示的方波信號展開為傅里葉級數。考慮到，可得得圖示信號的傅里葉級數展開式為它只含有一、三、五、…

…等奇次諧波分量。(a)基波(b)基波+三次諧波(c)基波+三次諧波+五次諧波(d)基波+三次諧波+五次諧波+七次諧波方波的組成看到，合成波形所包含的諧波分量愈多時，除間斷點附近外，它愈接近于原方波信號。在間斷點附近，隨著所含諧波次數的增高，合成波形的尖峰愈接近間斷點，但尖峰幅度并未明顯減小。可以證明，即使合成波形所含諧波次數時，在間斷點處仍有約9%的偏差，這種現象稱為吉布斯（Gibbs）現象。在傅里葉級數的項數取的很大時，間斷點處尖峰下的面積非常小以至于趨近于零，因而在均方的意義上合成波形同原方波的真值之間沒有區別。3.1.2奇、偶函數的傅里葉級數1．偶函數若被積函數是時間的偶函數，則波形對稱于縱坐標軸。當被積函數為偶函數時，在對稱區間的積分等于其半區間積分的二倍；而當被積函數為奇函數時，在對稱區間的積分為零，故得是偶函數是奇函數偶函數若被積函數是時間的奇函數，則波形對稱于原點。2．奇函數實際上，任意函數都可分解為奇函數和偶函數兩部分，即

需要注意，某函數是否為奇（或偶）函數不僅與周期函數的波形有關，而且與時間坐標原點的選擇有關。3.1.3傅里葉級數的指數形式傅里葉系數模相角傅里葉級數的指數形式為

傅里葉系數這就是求指數形式傅里葉級數的復系數的公式。表明，任意周期信號可分解為許多不同頻率的虛指數信號之和，其各分量的復數幅度（或相量）為。3.1.4典型周期信號的傅里葉級數1．周期矩形脈沖信號設周期矩形脈沖信號的脈沖寬度為，脈沖幅度為1，重復周期為T信號在一個周期內的表示式為可以求出各系數，其中直流分量余弦分量的幅度或寫作周期矩形信號展成三角形傅里葉級數其中為抽樣函數，它等于周期矩形信號的三角形式傅里葉級數為或若將展開指數形式的傅里葉級數，可得對稱方波信號是矩形的一種特殊情況，兩者相比較，對稱方波信號有兩個特點：所以可直接得到方波的傅里葉級數⑵對稱方波信號的脈沖恰好等于周期的一半，即⑴它是正負交替的信號，其直流分量（）等于零。或寫作對稱方波的傅里葉級數只包含基波和奇次諧波，也稱奇諧函數。2．周期鋸齒脈沖信號周期鋸齒脈沖信號是奇函數,因而，并可求出傅里葉級數的系數周期鋸齒脈沖信號的傅里葉級數為周期鋸齒脈沖信號的頻譜只包含正弦分量，諧波的幅度以的規律收斂。3．周期三角脈沖信號周期三角脈沖信號是偶函數，該信號的傅里葉級數周期三角脈沖的頻譜只包含直流、基波及奇次波頻率分量，諧波的幅度以的規律收斂。4．周期半波余弦信號周期半波余弦信號是偶函數，該信號的傅里葉級數周期半波余弦信號的頻譜只含有直流，基波和偶次諧波分量。諧波的幅度以規律收斂。5．周期全波余弦信號令余弦信號為則周期全波余弦信號為周期全波余弦信號的周期是的一半。周期全波余弦信號的傅里葉級數可見，周期全波余弦信號的頻譜包含直流分量及的基波和各次諧波分量，或者說，只包含直流分量及的偶次諧波分量。諧波的幅度以規律收斂。3.1.5MATLAB實現解：對于周期為4，脈寬為2，幅度為1的周期信號，首先建立fourier.m文件函數，其MATLAB程序如書P104。各種周期信號的傅里葉級數展開可以運用MATLAB來實現。例3-2周期矩形脈沖信號Fx=(2*sin(